Fun Geometry Problem with Solution #15
Blog นี้จะนำเสนอโจทย์ 2 ข้อ ที่อาจนำไปใช้เป็นทฤษฎีบทในการแก้โจทย์ข้ออื่นๆ ในอนาคต โจทย์ 1 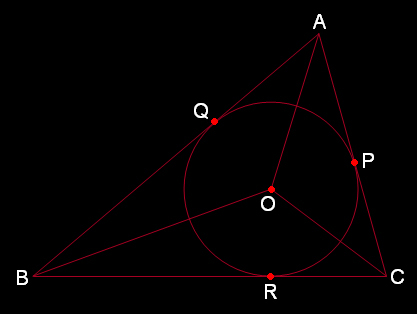 กำหนดให้ วงกลม O เป็นวงกลมแนบใน ∆ABC โดยมีจุด P, จุด Q และ จุด R เป็นจุดสัมผัส จงพิสูจน์ว่า AO, BO และ CO เป็นเส้นแบ่งครึ่ง ∠BAC, ∠ABC และ ∠ACB ตามลำดับ พิสูจน์ 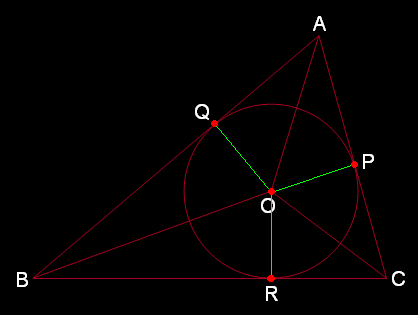 (1) ∵ OP และ OQ เป็นรัศมีของวงกลมเดียวกัน => OP = OQ (2) ∵ จุด P และ จุด Q เป็นจุดสัมผัส => ∠APO = 90° ∧ ∠AQO = 90° (3) จะเห็นว่า ∆AOP ≅ ∆AOQ ด้วยความสัมพันธ์แบบ ฉ-ด-ด (∠APO = ∠AQO = 90°, OP = OQ, AO = AO) => ∠OAP = ∠OAQ <=> AO เป็นเส้นแบ่งครึ่ง ∠BAC ใช้การพิสูจน์ในทำนองเดียวกัน จะได้ว่า BO และ CO เป็นเส้นแบ่งครึ่ง ∠ABC และ ∠ACB ตามลำดับ Q.E.D. โจทย์ 2  กำหนดให้ AO และ BO เป็นเส้นแบ่งครึ่ง ∠BAC และ ∠ABC ตามลำดับ จงพิสูจน์ว่า CO เป็นเส้นแบ่งครึ่ง ∠ACB (x = y) พิสูจน์  กำหนดจุด P, Q และ R บน AC, AB และ BC ตามลำดับ ที่ทำให้ OP ⊥ AC, OQ ⊥ AB และ OR ⊥ BC ตามลำดับ จะเห็นว่า ∆AOP ≅ ∆AOQ ด้วยความสัมพันธ์แบบ ม-ม-ด (∠APO = ∠AQO, ∠OAP = ∠OAQ, AO = AO) => OP = OQ ในทำนองเดียวกัน ∆BOQ ≅ ∆BOR => OQ = OR ∴ OP = OQ = OR => O เป็นจุดศูนย์กลางของวงกลมแนบใน ∆ABC โดยมีจุด P, จุด Q และ จุด R เป็นจุดสัมผัส => CO เป็นเส้นแบ่งครึ่ง ∠ACB (x = y) Q.E.D. Fun Geometry Problem with Solution #14
Blog นี้จะนำเสนอโจทย์ 4 ข้อ ที่อาจนำไปใช้เป็นบทตั้ง (Lemma) ในการแก้โจทย์ข้ออื่นๆ ในอนาคต โจทย์ 1 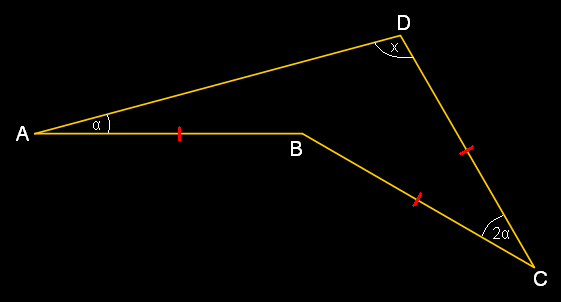 กำหนดให้ ☐ABCD เป็นสี่เหลี่ยมเว้า จงพิสูจน์ว่า x = 120° - α พิสูจน์  กำหนดจุด P บน AD ที่ทำให้ AP = CP สังเกตว่า ∆BCP ≅ ∆ABP ด้วยความสัมพันธ์แบบ ด-ด-ด (BC = AB, BP = BP, CP = AP) => ∠BCP = ∠BAP <=> ∠BCP = α <=> ∠DCP = α นอกจากนั้น ยังได้ว่า ∠BPC = ∠APB สังเกตว่า ∆CDP ≅ ∆BCP ด้วยความสัมพันธ์แบบ ด-ม-ด (CD = BC, ∠DCP = ∠BCP, CP = CP) => ∠CPD = ∠BPC ∴ ∠APB = ∠BPC = ∠CPD แต่ ∠APB + ∠BPC + ∠CPD = 180° <=> ∠CPD = 60° พิจารณา ∆CDP จะได้ว่า α + x + 60° = 180° <=> x = 120° - α Q.E.D. หมายเหตุ ☐ABCD เป็นสี่เหลี่ยมเว้า <=> ∠B > 180° <=> 360° - ∠A - ∠C - ∠D > 180° <=> 360° - α - 2α - (120° - α ) > 180° <=> α < 30° โจทย์ 2  กำหนดให้ ☐ABCD เป็นสี่เหลี่ยมเว้า จงพิสูจน์ว่า AB = BC = CD พิสูจน์  (1) ∵ BC = CD <=> ∆BCD เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด <=> ∠BDC = ∠CBD <=> ∠BDC = 90° - α <=> ∠ADB = 30° (2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ABD แนบใน <=> AO = BO ∧ ∠AOB = 2(∠ADB) <=> ∆ABO เป็น ∆หน้าจั่วที่มี ∠O เป็นมุมยอด ∧ ∠AOB = 60° <=> ∠BAO = ∠ABO = 60° ∴ ∆ABO เป็น ∆ด้านเท่า => BO = AB นอกจากนั้น O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ABD แนบใน <=> BO = DO ∧ ∠BOD = 2(∠BAD) <=> ∆BDO เป็น ∆หน้าจั่วที่มี ∠O เป็นมุมยอด ∧ ∠BOD = 2α <=> ∠DBO = ∠BDO = 90° - α (3) สังเกตว่า ∆BDC ≅ ∆BDO ด้วยความสัมพันธ์แบบ ม-ด-ม (∠CBD = ∠DBO, BD = BD, ∠BDC = ∠BDO) => BC = BO <=> BC = AB ∴ AB = BC = CD Q.E.D. โจทย์ 3  กำหนดให้ ☐ABCD เป็นสี่เหลี่ยมเว้า จงพิสูจน์ว่า AB = BC = CD พิสูจน์  (1) พิจารณา ∆ABC ∵ AB = BC <=> ∆ABC เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด <=> ∠BAC = ∠ACB ∵ ∠ABC = α + 2α + (120° - α) = 120° + 2α <=> ∠BAC = 30° - α ∧ ∠ACB = 30° - α <=> ∠CAD = 30° ∧ ∠ACD = 30° + α (2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACD แนบใน => CO = DO ∧ ∠COD = 2(∠CAD) <=> ∆CDO เป็น ∆หน้าจั่วที่มี ∠O เป็นมุมยอด ∧ ∠COD = 60° <=> ∠DCO = ∠CDO = 60° ∴ ∆CDO เป็น ∆ด้านเท่า => CO = CD ∧ ∠ACO = 30° - α นอกจากนั้น O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACD แนบใน <=> AO = CO <=> ∆ACO เป็น ∆หน้าจั่วที่มี ∠O เป็นมุมยอด <=> ∠CAO = ∠ACO <=> ∠CAO = 30° - α (3) จะเห็นว่า ∆ABC ≅ ∆ACO ด้วยความสัมพันธ์แบบ ม-ด-ม (∠BAC = ∠CAO, AC = AC, ∠ACB = ∠ACO) => BC = CO <=> BC = CD ∴ AB = BC = CD Q.E.D. โจทย์ 4  กำหนดให้ ☐ABCD เป็นสี่เหลี่ยมเว้า จงพิสูจน์ว่า x = α พิสูจน์  (1) ∵ BC = CD <=> ∆BCD เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด <=> ∠BDC = ∠CBD <=> ∠BDC = 90° - α <=> ∠ADB = 30° (2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ABD แนบใน => AO = BO = DO, ∠AOB = 2(∠ADB) = 60° และ ∠BOD = 2(∠BAD) = 2x ∵ AO = BO <=> ∆ABO เป็น ∆หน้าจั่วที่มี ∠O (= 60°) เป็นมุมยอด <=> ∠BAO = ∠ABO = 60° ∴ ∆ABO เป็น ∆ด้านเท่า => BO (= DO) = AB (= BC = CD) (3) สังเกตว่า ∆BDO ≅ ∆BCD ด้วยความสัมพันธ์แบบ ด-ด-ด (BO = BC, BD = BD, DO = DC) => ∠BOD = ∠BCD <=> 2x = 2α <=> x = α Q.E.D. Fun Geometry Problem with Solution #13
โจทย์ 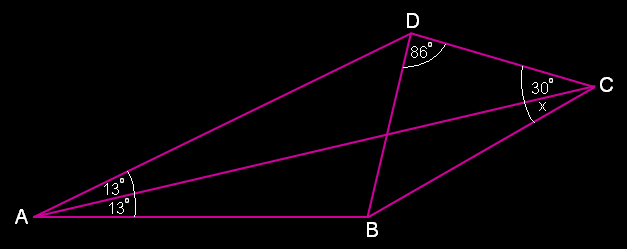 จงพิสูจน์ว่า x = 17° พิสูจน์  (1) ต่อ AB ออกไปยังจุด P โดยที่ AP = AD <=> ∆ADP เป็น ∆หน้าจั่ว ที่มี ∠A เป็นมุมยอด <=> ∠ADP = ∠APD <=> ∠APD = 77° (2) กำหนดให้จุด Q เป็นจุดตัดระหว่าง AC และ DP ∵ ∠DAQ = ∠PAQ <=> AQ เป็นส่วนสูงของ ∆ADP <=> DQ = PQ ∧ AQ ⊥ DP <=> DQ = PQ ∧ CQ ⊥ DP <=> ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด และมี CQ เป็นส่วนสูง => ∠PCQ = ∠DCQ <=> ∠PCQ = 30° <=> ∠DCP = 60° ∵ ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด และ ∠DCP = 60° <=> ∠CDP = ∠CPD = 60° ∴ ∆CDP เป็น ∆ด้านเท่า => CD = DP ∵ ∠CDP = 60° <=> ∠BDP = 26° <=> ∠DBP = 77° <=> ∠DBP = ∠BPD <=> ∆BDP เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด <=> BD = DP <=> BD = CD <=> ∆BCD เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด <=> ∠BCD = ∠CBD <=> ∠BCD = 47° <=> x = 17° Q.E.D. Fun Geometry Problem with Solution #12
โจทย์ 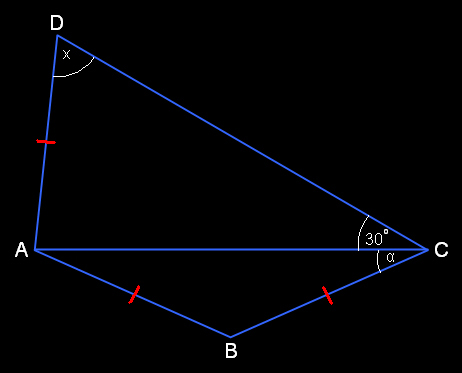 กำหนดให้ 0° < α < 60° จงพิสูจน์ว่า x = 90° - α พิสูจน์  (1) ∵ AB = BC <=> ∆ABC เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด <=> ∠BAC = ∠ACB <=> ∠BAC = α <=> ∠ABC = 180° - 2α (2) กำหนดจุด P บน CD ที่ทำให้ AB = BP <=> ∆ABP เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด <=> ∠BAP = ∠APB นอกจากนั้น BC = BP <=> ∆BCP เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด <=> ∠BPC = ∠BCP <=> ∠BPC = 30° + α <=> ∠CBP = 120° - 2α <=> ∠ABP = 60° <=> ∠BAP = 60° ∧ ∠APB = 60° ∴ ∆ABP เป็น ∆ด้านเท่า => AP = AB <=> AP = AD <=> ∆ADP เป็น ∆หน้าจั่ว ที่มี ∠A เป็นมุมยอด <=> ∠ADP = ∠APD <=> x = 180° - (∠APB + ∠BPC) <=> x = 90° - α Q.E.D. Fun Geometry Problem with Solution #11
โจทย์ 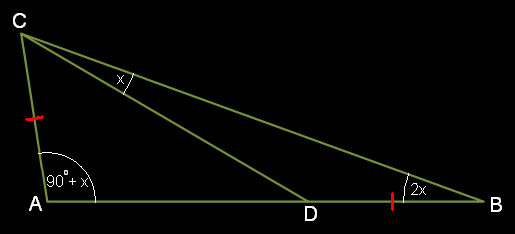 จงพิสูจน์ว่า x = 10° พิสูจน์  (1) ∠ADC = 3x (2) กำหนดจุด P บน BC ที่ทำให้ DP = BD <=> ∆BDP เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด <=> ∠BPD = ∠DBP <=> ∠BPD = 2x <=> ∠CDP = x <=> ∠CDP = ∠DCP <=> ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด <=> CP = DP => CP = BD (3) ต่อ BA ออกไปยังจุด Q โดยที่ CQ = AC <=> ∆ACQ เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด <=> ∠AQC = ∠CAQ <=> ∠AQC = 180° - ∠CAB = 90° - x นอกจากนั้น ยังได้ว่า CQ = BD พิจารณา ∆BCQ จะได้ว่า ∠BCQ = 90° - x <=> ∠BCQ = ∠BQC <=> ∆BCQ เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด <=> BQ = BC <=> BD + DQ = BP + CP <=> DQ = BP (4) กำหนดจุด R ภายใน ∆CDQ ที่ทำให้ ∠QDR = 2x และ ∠DQR = 2x <=> ∠CDR = x และ ∠CQR = 90° - 3x จะเห็นว่า ∆DQR ≅ ∆BDP ด้วยความสัมพันธ์แบบ ม-ด-ม (∠QDR = ∠DBP, DQ = BP, ∠DQR = ∠BPD) => DR = BD และ QR = DP <=> DR = DP และ QR = BD จะเห็นว่า ∆CDR ≅ ∆CDP ด้วยความสัมพันธ์แบบ ด-ม-ด (DR = DP, ∠CDR = ∠CDP, CD = CD) => CR = CP <=> CR = BD (5) จะเห็นว่า CQ = CR = QR <=> ∆CQR เป็น ∆ด้านเท่า => ∠CQR = 60° <=> 90° - 3x = 60° <=> x = 10° Q.E.D. |
TIYHz
 ผู้ติดตามบล็อก : 20 คน [?] ผู้ติดตามบล็อก : 20 คน [?] Group Blog All Blog
|
||
| Pantip.com | PantipMarket.com | Pantown.com | © 2004 BlogGang.com allrights reserved. | |||