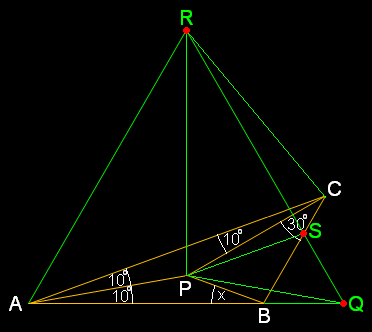
(1) ต่อ AB ออกไปยังจุด Q โดยที่ AQ = AC   ⇒   ∠CBQ = 60°

จะเห็นว่า ∆APQ ≅ ∆ACP ด้วยความสัมพันธ์แบบ ด-ม-ด (AQ = AC, ∠PAQ = ∠CAP, AP = AP)   ⇒   ∠AQP = ∠ACP   ⇔   ∠AQP = 10°   ⇔   ∠AQP = ∠PAQ   ⇔   ∆APQ เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   AP = PQ

พิจารณา ☐ACPQ จะได้ว่า ∠CPQ (มุมใหญ่) = 360° - 40°   ⇔   ∠CPQ (มุมเล็ก) = 40°

(2) กำหนดจุด R เหนือ AQ ที่ทำให้ AR = QR = AQ (= AC)   ⇔   ∆AQR เป็น ∆ด้านเท่า   ⇒   ∠QAR = 60° (⇔ ∠CAR = 40°), ∠AQR = 60° และ ∠ARQ = 60°

∵ AC = AR   ⇔   ∆ACR เป็น ∆หน้าจั่ว ที่มี ∠A (= 40°) เป็นมุมยอด   ⇔   ∠ARC (= ∠ACR) = 70°   ⇔   ∠CRQ = 10°

จะเห็นว่า ∆PQR ≅ ∆APR ด้วยความสัมพันธ์แบบ ด-ด-ด (PQ = AP, QR = AR, PR = PR)   ⇒   ∠PRQ (= ∠ARP) = (∠ARQ)/2 = 30°

(3) กำหนดจุด S เป็นจุดตัดระหว่าง BC กับ QR

∵ ∠QBS = ∠BQS = 60°   ⇒   ∆BQS เป็น ∆ด้านเท่า   ⇒   BQ = BS

∵ ∠PRS = ∠PCS   ⇔   ☐CRPS สามารถแนบในวงกลมได้   ⇔   ∠CPS = ∠CRS   ⇔   ∠CPS = 10°   ⇔   ∠QPS = 30°

สังเกตว่า BQ = BS และ ∠QBS = 2(∠QPS)   ⇒   จุด B เป็นจุดศูนย์กลางของวงกลมที่มี ∆PQS แนบใน   ⇒   BP = BQ   ⇔   ∆BPQ เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด   ⇔   ∠BPQ = ∠BQP   ⇔   ∠BPQ = 10°   ⇔   ∠ABP = x = 20°   Q.E.D.