โจทย์
กำหนดให้ ∠ACD เป็นมุมป้าน
จงพิสูจน์ว่า x = 6°
พิสูจน์
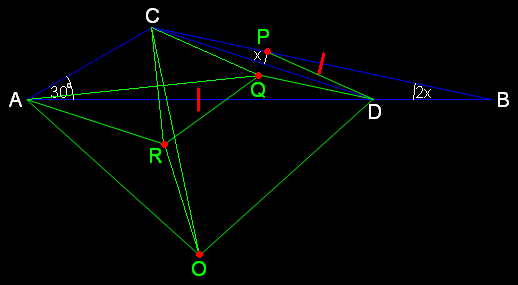
(1) พิจารณา ∆BCD จะได้ว่า ∠ADC = 3x
(2) กำหนดจุด P บน BC ที่ทำให้ DP = BD ⇔ ∆BDP เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด ⇔ ∠BPD = ∠DBP ⇔ ∠BPD = 2x ⇔ ∠CDP = x ⇔ ∠CDP = ∠DCP ⇔ ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด ⇔ CP = DP ⇒ CP = BD
(3) กำหนดจุด Q เหนือ AB ที่ทำให้ ∠DAQ = x และ ∠ADQ = 2x ⇔ ∠CAQ = 30° - x และ ∠CDQ = x
จะเห็นว่า ∆ADQ ≅ ∆BCD ด้วยความสัมพันธ์แบบ ม-ด-ม (∠DAQ = ∠BCD, AD = BC, ∠ADQ = ∠CBD) ⇒ AQ = CD และ DQ = BD
จะเห็นว่า ∆CDQ ≅ ∆CDP ด้วยความสัมพันธ์แบบ ด-ม-ด (DQ = DP, ∠CDQ = ∠CDP, CD = CD) ⇒ CQ = CP และ ∠DCQ = ∠DCP ⇔ CQ = BD และ ∠DCQ = x
พิจารณา ☐ADCQ จะได้ว่า ∠AQC (มุมใหญ่) = 360° - 5x ⇔ ∠AQC (มุมเล็ก) = 5x
(4) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACD แนบใน ⇒ ...
จุด O อยู่ใต้ AD
AO = CO = DO
∠AOC = 2(∠ADC) ⇔ ∠AOC = 6x
∠COD = 2(∠CAD) ⇔ ∠COD = 60°
∵ CO = DO และ ∠COD = 60° ⇒ ∆CDO เป็น ∆ด้านเท่า ⇔ CD = CO = DO ⇔ AQ = AO
นอกจากนั้น ยังได้ว่า ∠CDO = 60° ⇔ ∠ADO = 60° - 3x
∵ AO = DO ⇔ ∆ADO เป็น ∆หน้าจั่ว ที่มี ∠O เป็นมุมยอด ⇔ ∠DAO = ∠ADO ⇔ ∠DAO = 60° - 3x ⇔ ∠OAQ = 60° - 2x
(5) กำหนดจุด R เป็นภาพสะท้อนของจุด C ผ่าน AQ ⇒ ∆AQR ≅ ∆ACQ ⇒ ...
QR = CQ ⇔ QR = BD
∠QAR = ∠CAQ ⇔ ∠QAR = 30° - x ⇔ ∠OAR = 30° - x
∠AQR = ∠AQC ⇔ ∠AQR = 5x
สังเกตว่า ∆AOR ≅ ∆AQR ด้วยความสัมพันธ์แบบ ด-ม-ด (AO = AQ, ∠OAR = ∠QAR, AR = AR) ⇒ OR = QR ⇔ OR = BD
นอกจากนั้น ยังได้ว่า ∠AOR = ∠AQR ⇔ ∠AOR = 5x ⇔ ∠COR = x
(6) สังเกตว่า ∆COR ≅ ∆CDQ ด้วยความสัมพันธ์แบบ ด-ม-ด (OR = DQ, ∠COR = ∠CDQ, CO = CD) ⇒ CR = CQ
∴ CQ = CR = QR ⇔ ∆CQR เป็น ∆ด้านเท่า ⇒ ∠CQR = 60° ⇔ 10x = 60° ⇔ x = 6° Q.E.D.
หมายเหตุ เราสามารถแสดงว่าจุด Q อยู่ใน ∆ACD ได้ดังนี้
∵ ∠ACD เป็นมุมป้าน ⇒ 150° - 3x > 90° ⇔ x < 20° ⇔ ∠DAQ < 20°
∵ ∠DAQ < ∠CAD และ ∠ADQ < ∠ADC
∴ จุด Q อยู่ใน ∆ACD