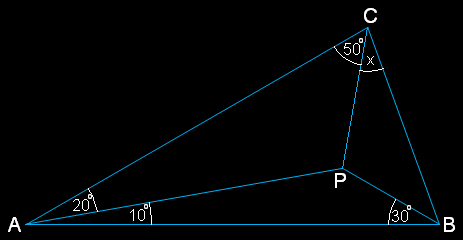จงพิสูจน์ว่า x = 30°

(1) พิจารณา ☐ABPC จะได้ว่า ∠BPC (มุมใหญ่) = 360° - 110°   ⇔   ∠BPC (มุมเล็ก) = 110°

(2) กำหนดจุด Q เป็นภาพสะท้อนของจุด P ผ่าน AB   ⇒   ∆ABQ ≅ ∆ABP   ⇒   AQ = AP, BQ = BP, ∠BAQ = ∠BAP = 10° และ ∠ABQ = ∠ABP = 30°

∵ BP = BQ และ ∠PBQ = 60°   ⇒   ∆BPQ เป็น ∆ด้านเท่า   ⇒   BP = PQ

(3) กำหนดจุด R บน AC ที่ทำให้ AR = AP

จะเห็นว่า ∆APR ≅ ∆APQ ด้วยความสัมพันธ์แบบ ด-ม-ด (AP = AQ, ∠PAR = ∠PAQ, AR = AP)   ⇒   PR = PQ   ⇔   PR = BP

∵ AP = AR   ⇔   ∆APR เป็น ∆หน้าจั่ว ที่มี ∠A (= 20°) เป็นมุมยอด   ⇔   ∠ARP (= ∠APR) = 80°

(4) กำหนดจุด S บน AR ที่ทำให้ PS = PR (= BP)   ⇔   ∆PRS เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   ∠PSR = ∠PRS   ⇔   ∠PSR = 80°

พิจารณา ∆CPS จะได้ว่า ∠CPS = 50°   ⇔   ∠CPS = ∠PCS   ⇔   ∆CPS เป็น ∆หน้าจั่ว ที่มี ∠S เป็นมุมยอด   ⇔   CS = PS

(5) กำหนดจุด T ทางด้านขวาของ CP ที่ทำให้ CT = PT = CP   ⇔   ∆CPT เป็น ∆ด้านเท่า   ⇒   ∠CPT = ∠CTP = 60°

จะเห็นว่า ∆PST ≅ ∆CST ด้วยความสัมพันธ์แบบ ด-ด-ด (PS = CS, PT = CT, ST = ST)   ⇒   ∠PTS (= ∠CTS) = (∠CTP)/2 = 30°

(6) สังเกตว่า ∆BCP ≅ ∆PST ด้วยความสัมพันธ์แบบ ด-ม-ด (BP = PS, ∠BPC = ∠SPT, CP = PT)   ⇒   ∠BCP = ∠PTS   ⇔   x = 30°   Q.E.D.

พิสูจน์ 2 (Angel Lazo HK)

(1) พิจารณา ☐ABPC จะได้ว่า ∠BPC (มุมใหญ่) = 360° - 110°   ⇔   ∠BPC (มุมเล็ก) = 110°

ให้ BP = L

(2) กำหนดจุด Q บน AB ที่ทำให้ PQ = L   ⇔   PQ = BP   ⇔   ∆BPQ เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   ∠BQP = ∠PBQ   ⇔   ∠BQP = 30°   ⇔   ∠APQ = 20°

(3) กำหนดจุด R บน AP ที่ทำให้ QR = L   ⇔   QR = PQ   ⇔   ∆PQR เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   ∠PRQ = ∠QPR   ⇔   ∠PRQ = 20°   ⇔   ∠AQR = 10°   ⇔   ∠AQR = ∠QAR   ⇔   ∆AQR เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   AR = QR   ⇒   AR = L

พิจารณา ∆PQR จะได้ว่า ∠PQR = 140°

(4) กำหนดจุด S บน AC ที่ทำให้ RS = L   ⇔   RS = AR   ⇔   ∆ARS เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   ∠ASR = ∠RAS   ⇔   ∠ASR = 20°   ⇔   ∠PRS = 40°

(5) ∵ QR = RS และ ∠QRS = 60°   ⇒   ∆QRS เป็น ∆ด้านเท่า   ⇒   ∠RQS = 60°   ⇔   ∠PQS = 80°

นอกจากนั้น ยังได้ว่า QS = QR (= L)   ⇔   QS = PQ   ⇔   ∆PQS เป็น ∆หน้าจั่ว ที่มี ∠Q (= 80°) เป็นมุมยอด   ⇔   ∠QPS (= ∠PSQ) = 50°   ⇔   ∠APS = 30°   ⇔   ∠CSP = 50°   ⇔   ∠CSP = ∠PCS   ⇔   ∆CPS เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   CP = PS

พิจารณา ∆PRS จะได้ว่า ∠PSR = 110°

(6) สังเกตว่า ∆BCP ≅ ∆PRS ด้วยความสัมพันธ์แบบ ด-ม-ด (BP = RS, ∠BPC = ∠PSR, CP = PS)   ⇒   ∠BCP = ∠RPS   ⇔   x = 30°   Q.E.D.

จงพิสูจน์ว่า x = 10°

(1) ∠CAP = 90° - 6x และ ∠APC = 90° + x

(2) กำหนดจุด Q บน AD ที่ทำให้ DQ = BD   ⇒   ...

♦ ∆CDQ ≅ ∆BCD ด้วยความสัมพันธ์แบบ ด-ม-ด (CD = CD, ∠CDQ = ∠BDC, DQ = BD)   ⇒   ∠DCQ = ∠BCD   ⇔   ∠DCQ = 2x   ⇔   ∠ACQ = 3x

♦ ∆DPQ ≅ ∆BDP ด้วยความสัมพันธ์แบบ ด-ม-ด (DP = DP, ∠PDQ = ∠BDP, DQ = BD)   ⇒   ∠DQP = ∠DBP   ⇔   ∠DQP = 3x   ⇔   ∠APQ = 2x

ให้ PQ = L

(3) กำหนดจุด R บน AP ที่ทำให้ QR = L   ⇔   QR = PQ   ⇔   ∆PQR เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   ∠PRQ = ∠QPR   ⇔   ∠PRQ = 2x   ⇔   ∠AQR = x

∵ ∠QAR = ∠AQR   ⇔   ∆AQR เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   AR = QR   ⇔   AR = L

∵ ∠PCQ = ∠PRQ   ⇔   ☐CPQR สามารถแนบในวงกลมได้   ⇔   ∠QCR = ∠QPR   ⇔   ∠QCR = 2x   ⇔   ∠ACR = x

นอกจากนั้น ยังได้ว่า ∠CQR = ∠CPR   ⇔   ∠CQR = 90° + x

(4) ต่อ CQ ออกไปยังจุด S โดยที่ RS = QR   ⇒   ∠RQS = 90° - x

∵ QR = RS   ⇔   ∆QRS เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   ∠QSR = ∠RQS   ⇔   ∠QSR = 90° - x

พิจารณา ∆CRS จะได้ว่า ∠CRS = 90° - x   ⇔   ∠CRS = ∠CSR   ⇔   ∆CRS เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด   ⇔   CR = CS

(5) กำหนดจุด T เป็นภาพสะท้อนของจุด R ผ่าน AC   ⇒   ∆ACT ≅ ∆ACR   ⇒   AT = AR = L, CT = CR, ∠CAT = ∠CAR = 90° - 6x และ ∠ACT = ∠ACR = x

สังเกตว่า ∆CRT ≅ ∆CRS ด้วยความสัมพันธ์แบบ ด-ม-ด (CR = CS, ∠RCT = ∠RCS, CT = CR)   ⇒   RT = RS   ⇔   RT = L

∴ AR = AT = RT   ⇔   ∆ART เป็น ∆ด้านเท่า   ⇒   ∠RAT = 60°   ⇔   180° - 12x = 60°   ⇔   x = 10°   Q.E.D.

จงพิสูจน์ว่า x = 30°

(1) กำหนดจุด P เป็นจุดตัดระหว่าง AC และ BD   ⇒   ∠ADP = 80° และ ∠BPC = 60°

(2) กำหนดจุด Q บน AB ที่ทำให้ PQ = BP   ⇔   ∆BPQ เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   ∠BQP = ∠PBQ   ⇔   ∠BQP = 40°   ⇒   ∠APQ = 20° และ ∠AQP = 140°

∵ ∠PAQ = ∠APQ   ⇔   ∆APQ เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   AQ = PQ

(3) กำหนดจุด R บน AD ที่ทำให้ PR = DP   ⇔   ∆DPR เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   ∠DRP = ∠PDR   ⇔   ∠DRP = 80°   ⇔   ∠APR = 40°   ⇔   ∠APR = ∠PAR   ⇔   ∆APR เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   AR = PR

(4) สังเกตว่า ∆PQR ≅ ∆AQR ด้วยความสัมพันธ์แบบ ด-ด-ด (PQ = AQ, PR = AR, QR = QR)   ⇒   ∠PQR (= ∠AQR) = (∠AQP)/2 = 70°

(5) สังเกตว่า ∆BCP ≅ ∆PQR ด้วยความสัมพันธ์แบบ ม-ด-ม (∠CBP = ∠PQR, BP = PQ, ∠BPC = ∠QPR)   ⇒   CP = PR   ⇔   CP = DP   ⇔   ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   ∠CDP = ∠DCP   ⇔   ∠CDP = x

∵ ∠DCP + ∠CDP = ∠BPC   ⇔   x + x = 60°   ⇔   x = 30°   Q.E.D.

จงพิสูจน์ว่า x = 20°

(1) ∠BPC = 100°

พิจารณา ☐ACBP จะได้ว่า ∠APB (มุมใหญ่) = 360° - 120°   ⇔   ∠APB (มุมเล็ก) = 120°

(2) กำหนดจุด O เป็น circumcenter ของ ∆BCP   ⇔   BO = CO = OP

นอกจากนั้น ยังได้ว่า ∠COP = 2(∠CBP)   ⇔   ∠COP = 20°

∵ CO = OP   ⇔   ∆COP เป็น ∆หน้าจั่ว ที่มี ∠O (= 20°) เป็นมุมยอด   ⇔   ∠CPO (= ∠OCP) = 80°   ⇔   ∠BPO = 20°

∵ BO = OP   ⇔   ∆BOP เป็น ∆หน้าจั่ว ที่มี ∠O เป็นมุมยอด   ⇔   ∠OBP = ∠BPO   ⇔   ∠OBP = 20°

(3) ให้ α = 10°

สังเกตว่า ☐ACOP เป็นสี่เหลี่ยมเว้า ที่มี CO = OP, ∠A = α, ∠O = 2α และ ∠C = 120° - α   ⇒   AP = CO (Click เพื่อดูวิธีพิสูจน์ในโจทย์ 2)   ⇔   AP = BO

(4) ต่อ PO ออกไปยังจุด Q โดยที่ BQ = BP   ⇔   ∆BPQ เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด   ⇔   ∠BQP = ∠BPQ   ⇔   ∠BQP = 20°   ⇔   ∠PBQ = 140°   ⇔   ∠OBQ = 120°

(5) สังเกตว่า ∆ABP ≅ ∆BOQ ด้วยความสัมพันธ์แบบ ด-ม-ด (AP = BO, ∠APB = ∠OBQ, BP = BQ)   ⇒   ∠ABP = ∠BQO   ⇔   x = 20°   Q.E.D.

จงพิสูจน์ว่า x = 10°

(1) ∠ABC = 50° และ ∠ADC = 50°

(2) กำหนดจุด P บน AB ที่ทำให้ CP = BC   ⇔   ∆BCP เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด   ⇔   ∠BPC = ∠CBP   ⇔   ∠BPC = 50°   ⇔   ∠ACP = 30°

(3) กำหนดจุด Q บน CD ที่ทำให้ AQ = AD   ⇔   ∆ADQ เป็น ∆หน้าจั่ว ที่มี ∠A เป็นมุมยอด   ⇔   ∠AQD = ∠ADQ   ⇔   ∠AQD = 50°   ⇒   ∠CAQ = 20° และ ∠DAQ = 80°

(4) สังเกตว่า ∆ACQ ≅ ∆ACP ด้วยความสัมพันธ์แบบ ม-ด-ม (∠CAQ = ∠CAP, AC = AC, ∠ACQ = ∠ACP)   ⇒   CQ = CP   ⇔   CQ = BC   ⇔   ∆BCQ เป็น ∆หน้าจั่ว ที่มี ∠C (= 140°) เป็นมุมยอด   ⇔   ∠CBQ (= ∠BQC) = 20°   ⇔   ∠ABQ = 30°

(5) กำหนดจุด R เป็นภาพสะท้อนของจุด Q ผ่าน AB   ⇒   ∆ABR ≅ ∆ABQ   ⇒   AR = AQ (= AD), BR = BQ, ∠BAR = ∠BAQ = 40° และ ∠ABR = ∠ABQ = 30°

∵ BQ = BR และ ∠QBR = 60°   ⇒   ∆BQR เป็น ∆ด้านเท่า   ⇒   BQ = QR

(6) สังเกตว่า ∆ADQ ≅ ∆AQR ด้วยความสัมพันธ์แบบ ด-ม-ด (AD = AR, ∠DAQ = ∠QAR, AQ = AQ)   ⇒   DQ = QR   ⇔   DQ = BQ   ⇔   ∆BDQ เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   ∠DBQ = ∠BDQ   ⇔   ∠DBQ = x

∵ ∠DBQ + ∠BDQ = ∠BQC   ⇔   x + x = 20°   ⇔   x = 10°   Q.E.D.