(1) ∵ AC = AD   ⇔   ∆ACD เป็น ∆หน้าจั่ว ที่มี ∠A (= 100°) เป็นมุมยอด   ⇔   ∠ACD = ∠ADC = 40°

(2) กำหนดจุด P เหนือ AB ที่ทำให้ ∠BAP = 40° (⇔ ∠CAP = 60°) และ ∠ABP = 40°

จะเห็นว่า ∆ABP ≅ ∆ACD ด้วยความสัมพันธ์แบบ ม-ด-ม (∠BAP = ∠ACD, AB = CD, ∠ABP = ∠ADC)   ⇒   AP = AC และ BP = AD

∴ AC = AP = BP

(3) ∵ AC = AP และ ∠CAP = 60°   ⇒   ∆ACP เป็น ∆ด้านเท่า   ⇒   AP = CP และ ∠APC = 60°

สังเกตว่า AP = BP = CP   ⇔   จุด P เป็นจุดศูนย์กลางของวงกลมที่มี ∆ABC แนบใน   ⇒   ∠ABC = (∠APC)/2   ⇔   x = 30°   Q.E.D.

(1) ∠CBD = 90° - α

(2) ต่อ BC ออกไปยังจุด Q โดยที่ BQ = AQ   ⇔   ∆ABQ เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   ∠BAQ = ∠ABQ   ⇔   ∠BAQ = 90° - α   ⇔   ∠AQB = 2α

นอกจากนั้น ยังได้ว่า ∠CAQ = 30°

(3) ต่อ AP ออกไปยังจุด R โดยที่ AR = AQ

จะเห็นว่า ∆ACR ≅ ∆ACQ ด้วยความสัมพันธ์แบบ ด-ม-ด (AR = AQ, ∠CAR = ∠CAQ, AC = AC)   ⇒   ∠ARC = ∠AQC   ⇔   ∠ARC = 2α

∵ AQ = AR และ ∠QAR = 60°   ⇒   ∆AQR เป็น ∆ด้านเท่า   ⇒   ∠AQR = 60° (⇔ ∠BQR = 60° - 2α) และ ∠ARQ = 60°

นอกจากนั้น ยังได้ว่า QR = AQ   ⇔   QR = BQ   ⇔   ∆BQR เป็น ∆หน้าจั่ว ที่มี ∠Q (= 60° - 2α) เป็นมุมยอด   ⇔   ∠BRQ (= ∠QBR) = 60° + α   ⇔   ∠BRP = α   ⇔   ∠BRP = ∠BCP   ⇔   ☐BPCR สามารถแนบในวงกลมได้   ⇔  ∠CBP = ∠CRP   ⇔   x = 2α   Q.E.D.

(1) ∠BDC = 150°

(2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆BCD แนบใน   ⇒   ...

     • BO = CO = DO

     • ∠BOC (มุมใหญ่) = 2(∠BDC)   ⇔   ∠BOC (มุมใหญ่) = 300°   ⇔   ∠BOC (มุมเล็ก) = 60°

     • ∠COD = 2(∠CBD)   ⇔   ∠COD = 2x

∵ BO = CO และ ∠BOC = 60°   ⇒   ∆BCO เป็น ∆ด้านเท่า   ⇔   BC = BO = CO

∴ AD = CO = DO

(3) ให้ AD = a และ CD = b

สังเกตว่า ∆CDO เป็น ∆หน้าจั่ว ที่มีฐานยาว b และด้านประกอบมุมยอดยาว a   ⇒   ∠COD = 24° (Click เพื่อดูวิธีพิสูจน์) ⇔   2x = 24°   ⇔   x = 12°   Q.E.D.

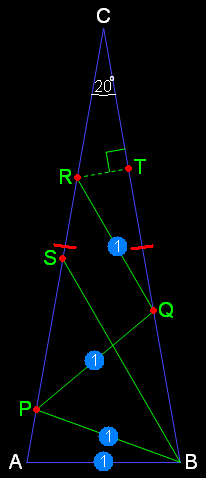
โดยไม่สูญเสียสาระสำคัญของกรณีทั่วไป เราสามารถสมมติให้ AB = 1

(1) ∵ AC = BC   ⇔   ∆ABC เป็น ∆หน้าจั่ว ที่มี ∠C (= 20°) เป็นมุมยอด   ⇔   ∠BAC = ∠ABC = 80°

(2) กำหนดจุด P บน AC ที่ทำให้ BP = 1   ⇔   BP = AB   ⇔   ∆ABP เป็น ∆หน้าจั่ว ที่มี ∠B เป็นมุมยอด   ⇔   ∠APB = ∠BAP   ⇔   ∠APB = 80°   ⇔   ∠ABP = 20°   ⇒   ∠CBP = 60° และ ∠BPC = 100°

(3) กำหนดจุด Q บน BC ที่ทำให้ PQ = 1   ⇔   PQ = BP

∵ BP = PQ และ ∠PBQ = 60°   ⇒   ∆BPQ เป็น ∆ด้านเท่า   ⇒   BQ = 1

นอกจากนั้น ยังได้ว่า ∠BPQ = 60°   ⇒   ∠CPQ = 40° และ ∠CQP = 120°

(4) กำหนดจุด R บน CP ที่ทำให้ QR = 1   ⇔   QR = PQ   ⇔   ∆PQR เป็น ∆หน้าจั่ว ที่มี ∠Q เป็นมุมยอด   ⇔   ∠PRQ = ∠QPR   ⇔   ∠PRQ = 40°   ⇔   ∠PQR = 100°   ⇔   ∠CQR = 20°   ⇔   ∠CQR = ∠QCR   ⇔   ∆CQR เป็น ∆หน้าจั่ว ที่มี ∠R เป็นมุมยอด   ⇔   CR = QR   ⇒   CR = 1

(5) กำหนดจุด S บน AC ที่ทำให้ BS = CS   ⇔   ∆BCS เป็น ∆หน้าจั่ว ที่มี ∠S เป็นมุมยอด   ⇔   ∠CBS = ∠BCS   ⇔   ∠CBS = 20°   ⇒   ∠PBS = ∠BSP = 40°   ⇔   ∆BPS เป็น ∆หน้าจั่ว ที่มี ∠P (= 100°) เป็นมุมยอด   ⇔   PS = BP   ⇔   PS = 1

พิจารณา ∆CQR ซึ่งเป็น ∆หน้าจั่ว เมื่อลากส่วนสูง RT จะได้ว่า ∆CRT และ ∆QRT เป็น ∆มุมฉาก ที่เท่ากันทุกประการ

โดยนิยามของ cosine ใน ∆มุมฉาก จะได้ CT = QT = cos20°   ⇒   CQ = 2cos20°

ในทำนองเดียวกัน สำหรับ ∆PQR และ ∆ABP จะได้ PR = 2cos40° และ AP = 2cos80° ตามลำดับ

ในทางกลับกัน สำหรับ ∆ABC และ ∆BCS จะได้ AC = 1/(2cos80°) และ CS = 1 + 1/(2cos20°) ตามลำดับ

∵ AC = BC   ⇔   AP + PR + CR = BC   ⇔   2cos80° + 2cos40° + 1 = 1 + 2cos20°   ⇔   cos20° = cos40° + cos80°   Q.E.D.

นอกจากนั้น ยังได้ว่า 1/(2cos80°) = 1 + 2cos20°   ⇔   2cos80° = 1/(1 + 2cos20°)   ⇔   AP = 1/(1 + 2cos20°)   ⇔   AC - CS - PS = 1/(1 + 2cos20°)   ⇔   BC - CS - PS = 1/(1 + 2cos20°)   ⇔   (1 + 2cos20°) - [1 + 1/(2cos20°)] - 1 = 1/(1 + 2cos20°)   ⇔   4cos³20° - 3cos20° = 1/2   ⇔   4cos³20° - 3cos20° = cos60°   Q.E.D.

(1) ∵ ☐ABCD เป็น ☐จัตุรัส   ⇒   AB = AD = BC = CD และ ∠BAD = ∠ABC = 90° (⇔ ∠DAP = ∠CBP = 75°)

∵ ∠BAP = ∠ABP   ⇔   ∆ABP เป็น ∆หน้าจั่ว ที่มี ∠P เป็นมุมยอด   ⇔   AP = BP

สังเกตว่า ∆ADP ≅ ∆BCP ด้วยความสัมพันธ์แบบ ด-ม-ด (AD = BC, ∠DAP = ∠CBP, AP = BP)   ⇒   DP = CP

(2) กำหนดจุด Q ภายใน ☐ABCD ที่ทำให้ ∠DAQ = 15° (⇔ ∠PAQ = 60°) และ ∠ADQ = 15°

จะเห็นว่า ∆ADQ ≅ ∆ABP ด้วยความสัมพันธ์แบบ ม-ด-ม (∠DAQ = ∠BAP, AD = AB, ∠ADQ = ∠ABP)   ⇒   AQ = AP และ DQ = BP

∴ AP = AQ = DQ

(3) ∵ AP = AQ และ ∠PAQ = 60°   ⇒   ∆APQ เป็น ∆ด้านเท่า   ⇒   AQ = PQ และ ∠AQP = 60°

สังเกตว่า AQ = DQ = PQ   ⇔   จุด Q เป็นจุดศูนย์กลางของวงกลมที่มี ∆ADP แนบใน   ⇒   ∠ADP = (∠AQP)/2   ⇔   ∠ADP = 30°   ⇔   ∠APD = 75°   ⇔   ∠APD = ∠DAP   ⇔   ∆ADP เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด   ⇔   DP = AD   ⇔   DP = CD

∴ CD = CP = DP   ⇔   ∆CDP เป็น ∆ด้านเท่า   Q.E.D.