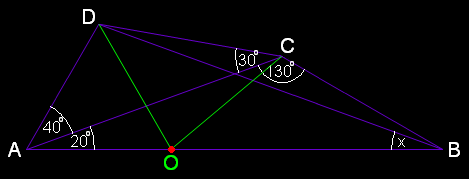
(1) ∠ABC = 30° และ ∠ADC = 110°

(2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACD แนบใน   ⇔   AO = CO = DO

นอกจากนั้น ยังได้ว่า ∠AOD = 2(∠ACD)   ⇔   ∠AOD = 60°

∵ AO = DO และ ∠AOD = 60°   ⇒   ∆ADO เป็น ∆ด้านเท่า   ⇔   AD = AO = DO   ⇔   AD = CO 

นอกจากนั้น ยังได้ว่า ∠DAO = 60°   ⇔   ∠DAO = ∠BAD   ⇒   จุด O อยู่บน AB

∵ AO = CO   ⇔   ∆ACO เป็น ∆หน้าจั่ว ที่มี ∠O เป็นมุมยอด   ⇔   ∠ACO = ∠CAO   ⇔   ∠ACO = 20°   ⇔   ∠BCO = 110°

(3) สังเกตว่า ∆BCO ≅ ∆ACD ด้วยความสัมพันธ์แบบ ม-ม-ด (∠CBO = ∠ACD, ∠BCO = ∠ADC, CO = AD)   ⇒   BC = CD   ⇔   ∆BCD เป็น ∆หน้าจั่ว ที่มี ∠C (= 160°) เป็นมุมยอด   ⇔   ∠CBD (= ∠BDC) = 10°   ⇔   ∠ABD = x = 20°   Q.E.D.

(1) พิจารณา ∆ABC จะได้ว่า ∠ABC = 30°

(2) กำหนดจุด P บน AB ที่ทำให้ CP ⊥ AB

พิจารณา ∆ACP จะได้ว่า ∠ACP = 70°

จะเห็นว่า ∆BCP เป็น ∆มุมฉาก ที่มี ∠P เป็นมุมฉาก และ ∠B = 30°   ⇒   BC = 2‧CP

(3) ต่อ AD ออกไปยังจุด Q โดยที่ AQ = AC   ⇔   ∆ACQ เป็น ∆หน้าจั่ว ที่มี ∠A (= 40°) เป็นมุมยอด   ⇔   ∠ACQ = ∠AQC = 70°

พิจารณา ∆ACD จะได้ว่า ∠CDQ = 70°   ⇔   ∠CDQ = ∠CQD   ⇔   ∆CDQ เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด   ⇔   CD = CQ

(4) กำหนดจุด R บน CQ ที่ทำให้ AR ⊥ CQ   ⇒   AR เป็นส่วนสูงของ ∆ACQ   ⇒   CR = QR

นอกจากนั้น ยังได้ว่า ∆ACR ≅ ∆ACP ด้วยความสัมพันธ์แบบ ม-ม-ด (∠ARC = ∠APC, ∠ACR = ∠ACP, AC = AC)   ⇒   CR = CP   ⇔   QR = CP

∴ CQ = 2‧CP   ⇔   CD = BC   ⇔   ∆BCD เป็น ∆หน้าจั่ว ที่มี ∠C (= 160°) เป็นมุมยอด   ⇔   ∠CBD (= ∠BDC) = 10°   ⇔   ∠ABD = x = 20°   Q.E.D.

จงพิสูจน์ว่า x = 10°

(1) กำหนดจุด P บน AB ที่ทำให้ ∠BPC = 40°   ⇔   ∠BPC = ∠CBP   ⇔   ∆BCP เป็น ∆หน้าจั่ว ที่มี ∠C เป็นมุมยอด   ⇔   CP = BC   ⇔   CP = AD

พิจารณา ∆ACP จะได้ว่า ∠ACP = 10°

(2) กำหนดจุด O เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACP แนบใน   ⇒   ...

     • AO = CO = OP

     • ∠AOP = 2(∠ACP)   ⇔   ∠AOP = 20°

     • ∠COP = 2(∠CAP)   ⇔   ∠COP = 60°

∵ AO = OP   ⇔   ∆AOP เป็น ∆หน้าจั่ว ที่มี ∠O (= 20°) เป็นมุมยอด   ⇔   ∠OAP (= ∠APO) = 80°

∵ CO = OP และ ∠COP = 60°   ⇒   ∆COP เป็น ∆ด้านเท่า   ⇒   OP = CP   ⇔   AO = AD   ⇔   ∆ADO เป็น ∆หน้าจั่ว ที่มี ∠A (= 80°) เป็นมุมยอด   ⇔   ∠AOD (= ∠ADO) = 50°   ⇔   ∠DOP = 30°   ⇔   ∠COD = 30°

(3) สังเกตว่า ∆CDO ≅ ∆DOP ด้วยความสัมพันธ์แบบ ด-ม-ด (CO = OP, ∠COD = ∠DOP, DO = DO)   ⇒   CD = DP   ⇔   ∆CDP เป็น ∆หน้าจั่ว ที่มี ∠D เป็นมุมยอด   ⇔   ∠DCP = ∠CPD   ⇔   ∠DCP = 40°   ⇔   ∠BDC = x = 80°   Q.E.D.

(1) ∵ [ABCDEFGHI] เป็นรูปเก้าเหลี่ยมด้านเท่ามุมเท่า   ⇒   AB = BC = CD = DE = a

นอกจากนั้น ยังได้ว่า ∠ABC = ∠BCD = ∠CDE = [(9 - 2) × 180°] ÷ 9 = 140°

จะเห็นว่า ∆CDE ≅ ∆ABC ด้วยความสัมพันธ์แบบ ด-ม-ด (CD = AB, ∠CDE = ∠ABC, DE = BC)   ⇒   CE = AC   ⇔   CE = b

∵ AB = BC   ⇔   ∆ABC เป็น ∆หน้าจั่ว ที่มี ∠B (= 140°) เป็นมุมยอด   ⇔   ∠BAC = ∠ACB = 20°

∵ CD = DE   ⇔   ∆CDE เป็น ∆หน้าจั่ว ที่มี ∠D (= 140°) เป็นมุมยอด   ⇔   ∠DCE (= ∠CED) = 20°   ⇒   ∠ACE = 100°

∵ AC = CE   ⇔   ∆ACE เป็น ∆หน้าจั่ว ที่มี ∠C (= 100°) เป็นมุมยอด   ⇔   ∠CAE = ∠AEC = 40°

(2) ต่อ EC ออกไปยังจุด P ที่ทำให้ CP = a   ⇒   ∠BCP = 60°

∵ BC = CP และ ∠BCP = 60°   ⇒   ∆BCP เป็น ∆ด้านเท่า   ⇒   BP = BC และ ∠CBP = 60°

สังเกตว่า AB = BC = BP   ⇔   จุด B เป็นจุดศูนย์กลางของวงกลมที่มี ∆ACP แนบใน   ⇒   ∠CAP = (∠CBP)/2   ⇔   ∠CAP = 30°

พิจารณา ∆AEP จะได้ว่า ∠APE = 70°   ⇔   ∠APE = ∠EAP   ⇔   ∆AEP เป็น ∆หน้าจั่ว ที่มี ∠E เป็นมุมยอด   ⇔   EP = AE   ⇔   a + b = c   Q.E.D.

(1) ให้ AE = a และ BE = b

∵ ∆ABC เป็น ∆ด้านเท่า   ⇒   AC = a + b, ∠BAC = 60° และ ∠ACB = 60° (⇔ ∠ACE = 60° - x)

∵ ∆BDE เป็น ∆ด้านเท่า   ⇒   DE = b และ ∠BED = 60° (⇒ ∠ADE = 60° - α และ ∠AED = 120°)

(2) กำหนดจุด P บน AC ที่ทำให้ AP = a   ⇔   CP = b

∵ AE = AP และ ∠EAP = 60°   ⇒   ∆AEP เป็น ∆ด้านเท่า   ⇒   EP = a และ ∠APE = 60° (⇔ ∠CPE = 120°)

(3) สังเกตว่า ∆CEP ≅ ∆ADE ด้วยความสัมพันธ์แบบ ด-ม-ด (EP = AE, ∠CPE = ∠AED, CP = DE)   ⇒   ∠ECP = ∠ADE   ⇔   60° - x = 60° - α   ⇔   x = α   Q.E.D.