|
|
| | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | |
|
| |
|
|
|
|
|
|
|
|
บบที่6
บทที่ 6 ครับ การทดสอบ ไคสแควร์
การทดสอบ ไคสแควร์ เป็นการทดสอบข้อมูลเชิงคุณภาพและ
ทดสอบข้อมูลเชิงปริมาณที่อยู่ในรูปความถี่
คำถามให้ดูแบบฝึกหัด สอนเสริมครั้งที่สอง
ข้อ 3 4 ก่อนเรียน-หลังเรียน
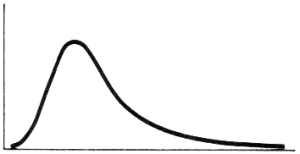
การแจกแจง ไคสแควร์ เป็นการแจกแจง ของข้อมูลต่อเนื่อง
ที่ไม่เป็นโค้งปกติ เรียกว่า โค้งไม่สมมาตร และ เบ้ไปทางขวา
^
^
อย่างนี้เรียกว่า เบ้ขวา คือส่วนมากจะกองอยู่ทางซ้าย แล้วลาดเทไปทางขวา
แบบนี้แหละ เป็นโค้งของ ไคสแควร์ เคยออกสอบ
6.1.2 อาจารย์บอกว่ามันยาก ไม่ออกสอบ ให้ผ่านไป
ถามต่อ ถ้าเกิดพลิกผัน ออกสอบมาทำไง ตอบ........ทำใจครับ
เรื่องนี้มันยาก ออกมา ก็ไม่มีใครทำได้ดอก อย่ากังวลไปเลย
(ผมเสียเวลาดูตั้งนาน แต่อาจารย์ บอกว่าไม่ออก เออ ไม่ออก ก็ไม่ออก)
6.1.3 นี่ออกสอบนะ อาจารย์บอก เปิดหนังสือดูด้วยครับ หน้า 6-18
เป็นการทดสอบ อัตราส่วน ว่ามันเป็นอย่างที่ว่าหรือปล่าว
ดูตัวอย่างหน้า 6- 19 ครับ
อัตราส่วน ที่คาดว่ามันจะเป็นคือ Ho เป็น 2:3:1
ถ้ามันไม่เป็น ก็ ปฏิเสธ Ho แล้วมายอมรับ H1 เท่านั้นเอง ง่ายๆ
ดูสูตรให้คุ้นตา นะครับ สูตรนี้ออกสอบ เขาจะให้มาใน หน้าแรกๆ ของข้อสอบ

ดูความหมายไว้ด้วย Oi คือ ค่าที่ได้จากการสังเกต O มาจาก Observed ครับ แปลว่าสังเกต
ส่วน E หมายถึง Expected เป็นค่าที่เราคาดหวัง ว่าอยากให้มันเป็น
ข้อสอบถามว่า การทดสอบความเป็นอิสระ ใช้ตัวสถิติอะไร
ตอบ.....ใช้ ไคสแควร์ 2
ถ้าข้อสอบออกเรียง บท เราน่าจะ เดาความได้ว่า นี่ เป็นเรื่อง ไคสแควร์นะ
ข้อสอบออกบทละ 6 ข้อ 15 บท รวม 90 ข้อ
ต้องผ่าน 54 ข้อ หรือ 60% จึงจะสอบผ่าน
ไคสแควร์ นี้เป็นการทดสอบ นอนพารามิเตอร์ (อ่านว่า นอน เสียงสั้นมากๆ)
แล้วไอ้คำว่า นอนพารามิเตอร์ เนี่ยมันอะไรกันล่ะ
ตอบ.......แปลว่า ตัวเลข หรือค่าสถิติ ที่เราได้มาจากการเก็บด้วยตัวเราเอง
จากกลุ่มเล็กๆ
ทีนี้ ถ้าเราได้ค่า ตัวเลขต่างๆมาจากประชากร เราจะเรียกตัวเลขนี้ว่า พารามิเตอร์
เอ้าขอตัวอย่างหน่อยดิ ได้คับ ตัวอย่างเช่น
การสำรวจจำนวนเด็กแรกเกิดใน กทม. ในปี 2551 ไง
เก็บหมดทุกคนที่คลอดครับ เก็บอายุแม่ เพศเด็ก เวลาเกิด อะไรพวกนี้ครับ
อย่างนี้ เป็นการเก็บตัวเลขจริงๆ จากโรงพยาบาลจริงๆ ทุกโรง
(แน่นอน มันอาจมีหลุดบ้าง แต่น้อยมากๆ เช่นคลอดเองที่บ้าน ช่างหัวมัน)
ค่าที่ได้ แบบนี้ มาจากจากการเก็บข้อมูล ใน กทม. ครบถ้วน
(สมมุติ)ได้ว่ามีเด็กเกิด ในปี 2551 สี่แสนแปดหมื่นคนนะ
แบบนี้แหละเราเรียกว่า ค่าพารามิเตอร์
หรืออีกอย่างเช่น ตัวเลข แสดง ปริมาณน้ำฝน ในปี 2550 ของกทม เก็บตัวเลข ไว้ทุกวัน
พอจะเอามาใช้ ก็กดคอมดู ได้ทุกเมื่อ อย่างนี้ เรียนว่า ค่าพารามิเตอร์
แล้วที่ไม่ใช่ค่าพารามิเตอร์ ล่ะ ก็เก็บเอง ในวงแคบๆ
หรือในพื้นที่เล็กๆ หรือ ในโรงงานของเราเอง
(โดยไม่มีการเก็บอย่างนี้มาก่อนในวงกว้าง )
มีการตั้ง การคาดหวัง หรือตัวเลขไว้ในใจซะก่อน
แล้วก็ เก็บตัวอย่างมา เช่น ตัวอย่างในหน้า 6 -21
เขาบอกว่า เขาเชื่อว่า สัดส่วนมันน่าจะเป็น 3 : 6:2:1 นะ
แล้วก็ไปเก็บข้อมูลมา จากกลุ่มตัวอย่าง ได้มา เป็น 120:250:120:110 คน
ก็เอา สัดส่วนของอย่างนี้ เข้าสูตร คำนวณซะ (การคำนวณไม่ออกสอบครับ)
แล้วเปิดตาราง
การเปิดตาราง นั้น ต้องรู้ค่า องศาของความเป็นอิสระ
องศาความเป็นอิสระนี่ เขาเปิดอย่างนี้นะครับ
ดูที่ โจทย์ยกมา คือมี อัตราส่วนอยู่ 4 อย่าง
แบบนี้ เราเรียกว่ามีค่าที่เราสังเกตอยู่ 4 แบบด้วยกัน
จึงบอกว่า มีค่า k อยู่เท่ากับ 4 นะ ก็เอาค่านี้ไปเปิดตาราง
ก่อนเปิดก็ เอา k - 1 ซะก่อน ถามว่า เอาหนึ่งมาลบทำไม
ตอบ............. ก็เรามี สิ่งที่จะสังเกตอยู่ 4 อย่าง
ทีนี้ ก็เลือกไปทีละอย่าง เลือกไปได้ 3 อย่าง เหลือ หนึ่งอย่าง
เป็นอย่างสุดท้าย ไอ้อย่างสุดท้ายนี้เราเลือกไม่ได้แล้วหละ
เราต้อง เอามันไว้ ไม่ว่าจะชอบหรือไม่ก็ตาม
ตรงนี้ แปลว่า มีสี่อย่าง เรามีอิสระเลือกได้ 3 อย่าง
อย่างที่สี่เลือกไม่ได้ จึงเรียกว่า เรามีอิสระในการเลือกเพียง 3 อย่างนะ
ตัวเลข 3 นี่ มันมาจาก เรื่องนี้แหละ (ใช้ตัวอักษร k แทนจำนวนอย่าง)
แต่เลือกได้ สามอย่างนะ ตัวสุดท้ายไม่ต้องเลือกแล้ว ต้องหยิบเลยครับ
จึงเขียนเป็นว่ามันอิสระอยู่ k - 1 ซะ
แล้วก้อเอาไปเปิดตารางราง หน้า 7-72 ครับ
ที่นี้จะเปิดได้ครบ เราต้องดูด้วยว่าโจทย์ บอกค่าความเชื่อมั่นว่าเป็นเท่าใด
ข้อนี้ (กิจกรรมข้อ 1 หน้า 6-21 ) โจทย์ บอกค่านัยสำคัญ 0.01
เราก็เอา ไปเปิดได้ ค่า ไคสแควร์ 2 เท่ากับ 11.3 (ลองเปิดตาราง ดูของจริงด้วยครับ)
ทีนี้ ค่าคำนวณได้ตามโจทย์ มันมีตั้ง 90.33 แน่ะ มากกว่ากันตั้งเยอะ
แปลผลว่า ไอ้ที่เราคิดไว้นั้นหน่ะ มันไม่จริงนะ ( ก้อ.... เท่านั้น)
จึงปฏิเสธ Ho ไปซะ แล้วมายอมรับ H1
แค่นี้ครับ ไม่มีอะไรอีก จบเรื่อง การทดสอบอัตราส่วน ด้วย ไคสแควร์
6.1.4 ทดสอบความเป็นอิสระ โดยใช้ ไคสแควร์
คำนวณไม่ออก ขืนออกมา ก็สอบตกยกชั้น ครับ
เอาหลักการก็แล้วกัน เรื่องนี้ คนที่ทดสอบ
เขาอยากรู้ว่า ของสองอย่างมีความสัมพันธ์ กันหรือไม่
หรือ การเลือกซื้อสินค้าบางอย่าง มีความสัมพันธ์ กับอายุ หรือเพศชายหญิงหรือไม่
เขาจะใช้ ไคสแควร์ มาทดสอบ ตรงนี้ขอข้าม การคำนวณไป
เอาผลที่คำนวณออกมาแปลผลกัน
สมมุติ ว่า คำนวณได้ 2.24 ตาม ตัวเลขหน้า 6-24
ค่าที่เปิดได้ในตารางคือ 9.49
เรามาแปลผลกัน ณ ตรงนี้ เราได้ ค่าที่คำนวณมา น้อยกว่าค่า ที่เปิดได้ในตาราง
แปลว่า สิ่งที่นำมาทดสอบกันนั้น
มัน เป็นอิสระต่อกัน หรือ พูดอีกอย่างหนึ่งว่ามัน ไม่มีความสัมพันธ์กัน
^
^
ข้อความนี้ ขอให้จดจำให้ดี
ขอให้เพื่อนนักศึกษา จดจำ การแปลผลนี้ให้แม่นนะครับ
ผมจดจำโดย นึกภาพในใจ เป็นกราฟ ของไคสแควร์
มันจะมีหางของกราฟทางขวามือเป็นสีเข้ม
และส่วนใหญ่ทาง ซ้ายมือ เป็นโล่งๆ (ที่เรียกว่าพื้นที่ใต้กราฟ)
เส้นแบ่ง ระหว่าง สีเข้ม กับพื้นที่โล่งๆ เรียกว่า เส้นวิกฤติ
คือ ค่า ที่เราเปิดได้ในตารางนั่นเอง ถ้าเราได้น้อยกว่าค่านี้
แปลว่า เป็นอิสระต่อกัน เทคนิคนี้ ผมจำว่า มันอยู่ในที่โล่ง มันจึงเป็นอิสระ
ในทางตรงกันข้าม ถ้าค่าที่คำนวณได้ ตกอยู่ในเขต สีเข้ม
สีเข้มเป็นพื้นที่เล็กๆแคบๆ มันไม่เป็นอิสระ ง่ายๆ เท่านี้จริงๆ
จบ เรื่อง การทดสอบ ความเป็นอิสระ
6.2 การทดสอบ นอนพาราเมตริก
6.2.1 แนวคิดนอนพาราเมตริก
ใช้ทดสอบกับสมมติฐาน ที่ไม่ขึ้นกับการแจกแจง หรือ ไม่เกี่ยวข้องกับ ตัวพารามิเตอร์
ทีนี้ แบบนอนพารามิเตอร์ กับ แบบพารามิเตอร์ นั้น
แบบพารามิเตอร์ จะน่าเชื่อถือมากกว่า
ตัวอย่างนอนพาราในเรื่องนี้คือ ความชอบไม่ชอบ ชอบมากชอบน้อย
พวกสอบถาม ทัศนะคติต่างๆ รวมถึงแบบประเมิน ที่เราจะต้องกรอก
ในวันไปฟังสอนเสริม ด้วย จะเห็นว่าเขาให้ระบายช่อง 1 5 ด้วย ว่า
ดีมากน้อยเพียงใด พอใจเพียงใด อย่างนี้เป็น นอนพาราเมตริกครับ
แล้วที่ไม่ใช่ นอนพาราล่ะ ก็อายุไง ความสูงไง น้ำหนักไง
(ถามแบบนี้สาวๆ ไม่อยากตอบ) ถ้าเก็บไปเยอะๆ ครบทุกคนที่เรียน มสธ ปุ๊บ
เราจะเรียกตัวเลข อายุ ความสูง น้ำหนัก นี่เป็น พาราเมตริกครับ
จะเห็นว่า มันนับได้ วัดได้ และมีขอบเขตแน่นอน บอกให้ใคร
ใครก็รู้และแปลผลได้อย่างเดียวกัน
ส่วน ความชอบไม่ชอบ ความพร้อมไม่พร้อม นี่ มันวัดเป็นตัวเลข เป๊ะๆไมได้
ความชอบ ที่ถาม จากคนสองคน ก็นำมาเทียบกันไม่ได้ นำมาชั่งกิโลไม่ได้
นำไม้เมตรมาวัดไม่ได้ แบบนี้ เป็นนอนพารามิเตอร์ครับ
6.2.2 การทดสอบโดยใช้เครื่องหมาย
การทดสอบแบบนี้ ต้องมาจากข้อมูล คู่เดียวกัน
เช่นการทดสอบว่า พนักงานจะมียอดขายสินค้าได้มากขึ้นหรือไม่
เขาจะให้เครื่องหมาย ถ้ามากขึ้น กว่าเดิม ก็ใส่บวก ถ้าน้อยก็ใส่ลบ ถ้าเท่าเดิม ก็ใส่ ศูนย์
หรืออยากรู้ว่า ก่อน และหลังการฝึกอบรม หรือนักศึกษา
สามารถทำแบบฝึกหัดได้คะแนนมากขึ้นหรือไม่
หลังจากอ่านหนังสือ ชุดวิชา32206 จบบทแล้ว ว่าเราเข้าใจหรือไม่ เขาก็จะเอาคะแนนมาเทียบกัน
หรือเป็นการนำคะแนน หรือตัวเลขยอดขาย ก่อนและหลัง มาดูกัน ทีละคู่
ให้ดูตารางในหนังสือหน้า 6-37 ประกอบไปด้วยครับ
จะเห็นว่า เขา ทำเครื่องหมาย + - 0 ไว้ด้วย
แบบนี้แหละ ที่เรียกว่า นอนพารามิเตอร์ อย่างหนึ่ง
แล้วนำจำนวนเครื่องหมายเหล่านี้ไปคำนวณ (การคำนวณไม่ออกสอบ)
ตารางที่เปิดนี้ เราจะเปิดตาราง หน้า 7-71 ครับ ไม่ใช้ไคสแควร์
เป็นตารางการแจกแจง แบบทวินาม ( < -----.ชื่อไม่คุ้นเลย ช่างมัน จำเอาไว้ก่อน)
ที่ต้องเปิดตารางนี้ เพราะมีการเก็บข้อมูล มาเป็นคู่
แบบ ก่อน กะหลัง ครับ คู่ ก็หมายถึงสอง
ทวิ ก็แปลว่าสอง
ค่าในตาราง เป็นค่าของ ความเชื่อมั่นสะสม
สะสมอะไร ตอบ สะสม ว่า สิ่งที่เรา นำมาทดสอบนั้น มันไม่ต่างกันนะ
ถ้าค่าในตารางมีค่าน้อยๆ แปลว่ามันต่างกัน
ให้ดูตารางประกอบครับ ค่า n คือจำนวนตัวอย่างที่เราเลือกมา
แล้ว x คือ ค่าเครื่องหมาย + ที่เราอยากให้มันเป็น (คือเราอยากให้มีการผลิตได้มากขึ้น)
มันมากขึ้นเราก็ใส่ + ซะ
ทีนี้ มาดู มีค่าที่เป็นบวกถึง 10 คน ใน 15 คน โดยมีคนไม่เพิ่มไม่ลดอยู่ 3 คน
อย่างนี้ เราน่าจะบอกได้โดยสามัญสำนึกแล้วว่า
มันดีกว่าเดิม แหง๋ๆ แต่ฝรั่งไม่เอาอย่างนี้ ฝรั่ง ก็สร้างตัวเลขขึ้นมา
สร้างตารางขึ้นมา แล้วให้เราเอามาเทียบซะ
เทียบแล้ว จะเห็นว่า เป็นไปตามนั้น
เป็นไปตามนั้น น่ะ เป็นแบบไหน ก็เป็นแบบที่ว่า
มันดีขึ้นไง รู้ได้ไง ตอบ ก็คาดเอาซิครับ จากตารางเราก็มองเห็นทิศทางอยู่
ว่ามันดีขึ้น
ทีนี้วิธีใช้ตาราง แบบฝรั่งนั้น ให้
นับใหม่ว่า 15 คน เพิ่ม 10 ลด 2 คน เฉยๆ 3 คน
นับเฉพาะ คนเพิ่ม กะคน ที่ลด มี 10 + 2 คน รวมเป็น 12 คน
เอาตัวเลข 12 คนนี่ไปเปิดตาราง หน้า 7-71 เทียบกับ 10
เราจะได้ตัวเลข .0193 ออกมา ตัวเลขนี้ บอกเราว่า มันมีโอกาส
ที่จะไม่เป็นไปตามนั้น อยู่ .0193 ส่วน ในหนึ่งส่วนนะ
เอา 1.0 - 0.0193 ได้ 0.9807 หรือ 98.07 % จะเป็นไปตามที่เราคาด
ทีนี้ โจทย์ให้ตัวเลขระดับนัยสำคัญมา ว่า 0.05 นะ แปลว่า
1 0.05 = 0.95 หรือ 95 % นั่นเอง
เรา เปิดตาราง แล้ว แปลกลับ ได้ตั้ง 98.07 % แน่ะ อย่างนี้ ชัวร์ ป้าบบบ
ว่าเราคิดถูก
มาดูสมมติฐานในหน้า 6-37 กัน
เขาตั้ง Ho ว่า ไม่แตกต่างกัน โดยมีความเชื่อมั่น 95 %
ส่วนที่เราเปิดได้ มัน หลุดไปที่ 98.07 % ก็แปลว่า Ho ไม่ถูก
ต้องปฏิเสธ Ho แล้วหันมายอมรับ Hi ครับ
แปลเป็นภาษาชาวบ้านว่า มันแตกต่างกัน แบบดีขึ้นเห็นๆ
( อ่านแล้วเข้าใจยากจัง ...... ครับ เข้าใจยาก ตรงนี้ ถ้าไม่ไหว
คำแนะนำของผมคือ ยอมทิ้งดีกว่า ข้ามไปก็ได้ครับ ข้อเดียวเอง)
แล้วค่อยไปเก็บเอาในส่วนอื่น อย่างไรเสีย น่าจะสอบผ่าน
อาจารย์ บอกว่า ไม่ออกคำนวณ ดังนั้น
ควรจำเพียงว่า การใช้เครื่องหมาย เป็นการทดสอบ ทวินาม
เป็น นอนพารามิเตอร์ ใช้ทดสอบ ว่า ก่อนกะหลังการอ่าน หรือฝึกบางอย่างแล้ว
ผลมันดีขึ้นกว่าเดิมหรือปล่าว
ทดสอบเมื่อประชากรสองชุด หรือชุดเดียวแต่สองครั้ง ไม่มี การแจกแจงเป็นแบบปกติ
^
^
จำไว้ครับ น่าจะออกสอบ
6.2.3 การทดสอบโดยใช้อันดับ และเครื่องหมาย
แนวคิดนี้ เป็นของ นักสถิติที่ชื่อ Wilcoxon ครับ เขียนเป็นภาษาไทยว่า
วิลคอกส์สัน อาจออกสอบ จำชื่อไว้หน่อยก็ดี สาระสำคัญ ย่อๆคือ
นำตัวเลขคะแนน นักเรียน หรือ ผลผลิตของคนงานแต่ละคน ก่อนกะหลัง
การฝึกปฏิบัติ มาเทียบกัน ว่าเพิ่มหรือลด แล้วใส่ตัวเลขที่เพิ่มหรือลด
ลงไปในตาราง แล้วคำนวณ ลำดับที่ออกมา คือใครได้งานออกมามาก
จะได้ที่หนึ่ง สอง สาม ลดหลั่นลงไปตามลำดับ
ถ้าได้ตัวเลข ของผลงานเท่ากัน ก็เอาตัวเลขมาเฉลี่ยกันซะ รายละเอียด
ดูที่ บรรทัด ล่างสุดหน้า 6 42 ครับ
พอได้อันดับมา ก็เอาอันดับ กะเครื่องหมายมาคิดคำนวณ ด้วย
จะเห็นว่า มีสองอย่างที่เขาเอามาใช้ คือ อันดับ หรือลำดับ เก่งไม่เก่ง
ทำได้มากน้อย เรียงลดหลั่นกันลงมา ถ้าเพิ่ม ให้เป็นเครื่องหมายบวก
ถ้าลดให้เป็นเครื่องหมายลบ กำกับไปด้วย
แล้วเอาอันดับ ทางบวกมารวมกัน เอาอันดับทางลบมารวมกัน
รวมแล้ว อย่างไหน น้อย เอาอย่างนั้นไปใช้
ดูข้อความ ในบรรทัดสุดท้ายหน้า 6 -41 ครับ ตรงนี้แหละ เป็นหัวใจ
เขาเอาไปถามเป็นคำถามครับ คำถามก็แบบคำถามข้อ 8 หน้า 42
ในแบบประเมิน ก่อนเรียนครับ ข้อ 8 นี่ คำตอบคือข้อ จ.
เขาเขียนว่า
จ. ค่าผลต่างที่ไม่ผิดเครื่องหมายที่มีค่าน้อยสุดจะได้ค่าต่ำสุด
เขาพิมพ์ผิดครับ ที่ถูกต้องเป็น
จ. ค่าผลต่างที่ไม่ ติด เครื่องหมายที่มีค่าน้อยสุดจะได้ค่าต่ำสุด
เอาหละ จำแค่นี้พอ ไม่มีคำนวณครับ
สรุป จำสอง จุดคือ
1. ชื่อ วิลคอกส์สัน กะ
2. ค่าผลต่างที่ไม่ ติด เครื่องหมายที่มีค่าน้อยสุดจะได้ค่าต่ำสุด
6.2.4 การทดสอบโดยใช้ผลรวมของตำแหน่งที่
ใช้ทดสอบความแตกต่าง ระหว่างค่าเฉลี่ยของประชากรสองชุด
เมื่อประชากร ชุดใดชุดหนึ่ง หรือทั้งสองชุดไม่มีการแจกแจงแบบปกติ
ดูคำถามข้อ 9 หน้า 42 ในแบบประเมินก่อนเรียนครับ ตอบข้อ ข.
ดูสูตรด้วย คำถามหลังเรียน ข้อ 9 เช่นกัน Ho ใช้คำว่า ไม่แตกต่างกัน
คำว่าไม่แตกต่างกัน คนที่เคยติวกับผมมา จะรู้ว่า มันมีสองทาง
พอมีสองทาง จะใช้เครื่องหมายเท่ากับ ( = ) เรื่องนี้ ไม่มีกำลังสอง
ดังนั้น ข้อ ค. ถูก ดูสูตรหน้า 6-47 หรือ แบบประเมินหน้า 44 ครับ
6.2.5 การทดสอบโดยใช้ค่าสหสัมพันธ์ ตำแหน่ง
เป็นเรื่องของตำแหน่ง เราก็ใช้กับ ข้อมูลเชิงคุณภาพนะครับ เคยออกสอบ
ดูแบบประเมิน ก่อนเรียน หน้า 42
(ขอให้อ่าน ที่หน้า 6-54 ตรงห้าบรรทัดแรก แล้ว ย่อความไว้ซะ + จดจำให้ได้ครับ)
หลักการคือ เรื่องเดียวหรือสิ่งเดียวกันกัน เอามาจัดอันดับที่ หรือเรียงตำแหน่งที่
โดยคนความเห็นของคนสองกลุ่ม
หรือ คะแนนนักเรียน ยี่สิบ สามสิบคน สอบไปสองวิชา
เช่นสอบ เลข กะสอบวิทย์ ไป
นำลำดับที่ของนักเรียนชุดนี้ ในแต่ละวิชามาเปรียบเทียบกัน
ว่ามันไปในทางเดียวกันหรือปล่าว ถ้าไปในทางเดียวกัน
เราบอกว่า มันสัมพันธ์กัน (เข้าสูตรคำนวณออกมา เป็นตัวเลข)
ถ้าไปคนละทิศ เราอาจบอกว่า มันสัมพันธ์กันในทางตรงกันข้าม
ตัวเลขที่นำลำดับที่มาคำนวณนี้ จะอยู่ระหว่าง -1 ถึง +1 เท่านั้น
เนื่องจากเป็นแนวคิดของการใช้ค่า สหสัมพันธ์ ซึ่งเป็นแบบเดียวกับ
เรื่อง ในหัวข้อ 4.2.2 ครับ หน้า 4-47 ขอให้กลับไปอ่านดู
หรือเข้าไปดูใน สรุปที่ผมเขียนไว้ให้แล้ว
ต่างกันตรงที่ใช้สูตรคนละสูตรเท่านั้น ส่วนการแปรผลเป็นแบบเดียวกัน
เจ้าของความคิดนี้คือ สเปียร์แมน ชื่อนี้ก็ต้องจำครับ เขาเก็บไปออกข้อสอบได้
กรุณาอย่าจำชื่อสับสน กับคนแรกที่ชื่อว่า วิลคอกส์สันนะครับ
เรียกการทดสอบแบบนี้ว่า
วิลคอกส์สัน นี่ คิดเรื่อง ลำดับ กะเครื่องหมาย สองอย่างรวมกันนะครับ
เพื่อทดสอบ ว่าสิ่งที่เรานำมาทดสอบ หรือที่เราสนใจนั้น มันแตกต่างกันหรือไม่
สเปียร์แมน นี่คิดเรื่อง สหสัมพันธ์ ตำแหน่ง
แปลเป็นไทยว่า เขาจะบอกได้ว่า ถ้าเก่ง อย่างเลข แล้ว น่าจะเก่ง วิทย์ด้วยหรือไม่นั้น
เขาจะบอกโดยใช้สูตรที่เขาคิดขึ้นมานี่แหละ
เทคนิคการจำของผมคือ สเปียร์แมน กะ สหสัมพันธ์ มี ตัว ส.เสือเหมือนกัน
ก็จำว่า สเปียร์แมน นี่เป็นคนคิด สหสัมพันธ์ ตำแหน่ง นะ จบแล้วครับ บทที่หก นี่ เข้าใจยากจริงๆ
คนที่สอบไปแล้ว เขาบอกว่า ไม่ค่อยออกคำนวณ ออกทฤษฎี มากกว่า ผมก็สรุปมาให้แบบที่เขาว่ามาครับ
| Create Date : 06 เมษายน 2552 |
| Last Update : 6 เมษายน 2552 19:47:41 น. |
|
4 comments
|
| Counter : 6602 Pageviews. |
 |
|
|
| โดย: Daeng IP: 58.137.14.198 วันที่: 24 เมษายน 2552 เวลา:13:42:15 น. |
|
|
|
| โดย: kkk IP: 113.53.90.106 วันที่: 22 ธันวาคม 2552 เวลา:17:50:36 น. |
|
|
|
| โดย: ดวงดาว IP: 118.173.33.253 วันที่: 27 มีนาคม 2553 เวลา:0:46:38 น. |
|
|
|
| โดย: nan IP: 183.89.226.235 วันที่: 19 มิถุนายน 2554 เวลา:22:43:16 น. |
|
|
|
|
|
|
|