|
ทดลองเล่นกับกฎของคลื่นเสียงที่มาถึงก่อน
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
Law of the first wavefront หรือ precedence effect (บางทีเรียก Haas effect) บอกว่า ถ้าคลื่นเสียงที่คล้ายกัน 2 ตัวเดินทางมาถึงผู้ฟังในเวลาไล่เลี่ยกัน ทิ้งห่างกันไม่เกิน 50 ms ผู้ฟังจะได้ยินเสียงแรก แต่ไม่ได้ยิน (suppress) เสียงหลัง ถึงแม้เสียงหลังจะดังกว่าถึง 10 dB แต่ถ้าเวลาทิ้งห่างกันมากกว่า 65 ms (หรือทิ้งห่างกันประมาณ 20 เมตรในอากาศ) เราจะได้ยินเสียง echo ชัดเจน นี่เป็นเหตุผลว่าทำไม เราไม่ได้ยินเสียง echo ในห้องเล็ก ๆ
ปรากฎการณ์นี้ทดลองเล่นง่าย ๆ ได้ด้วยสคริปต์นี้ ลองอัดเสียงสักหนึ่งพยางค์ (ในตัวอย่างคือไฟล์เสียง so.wav) โค้ดจะเล่นเสียงที่มี echo ซึ่งมีระยะเวลา delay ห้าค่าคือ 10 ms, 30 ms, 50 ms, 70 ms และ 90 ms พอดีเลย์เริ่ม 50 ms เราก็เริ่มได้ยินเสียง 2 ครั้งล่ะ

โน้ต เทคนิคการซ่อนข้อมูลในเสียงแบบเบสิกสุด ๆ อันหนึ่งคือ echo hiding เราใส่ echo เข้าไปในเสียงด้วยเวลาดีเลย์ที่แตกต่างกันในแบบที่สามารถตีความเป็นไบนารี่ดิจิท (ไม่จำเป็นต้องใส่ echo ตัวเดียว อาจจะใส่หลายตัว หรือใช้รูปแบบที่แตกต่างกันของ reverbertation ก็ได้) และเวลาดีเลย์นั้นไม่มากพอที่หูคนจะสามารถแยก echo ออกจาก host
| Create Date : 25 กรกฎาคม 2558 | | |
| Last Update : 25 กรกฎาคม 2558 20:15:09 น. |
| Counter : 2915 Pageviews. |
| |
|
 |
|
|
|
ทดลองเล่นกับ pitch ของ complex tones
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
ANSI นิยาม "pitch คือลักษณะเฉพาะ (attribute) ของการรับรู้เสียงในพจน์ที่เสียงสามารถเรียงลำดับบนสเกลจากต่ำไปสูง pitch ขึ้นอยู่กับองค์ประกอบความถี่ของเสียงกระตุ้นเป็นสำคัญ ไม่เพียงเท่านั้น ยังขึ้นอยู่กับความดันเสียงและรูปคลื่นของตัวกระตุ้น"
นิยามที่พอเห็นภาพง่ายกว่านั้น ว่า pitch เป็นลักษณะของการรับรู้เสียงที่ความแตกต่างของมันสัมพันธ์กับทำนองเพลง พูดอีกอย่างหนึ่งว่า เสียงใดก็ตามที่ให้การรับรู้เกี่ยวกับ pitch (หรือ เสียงใดก็ตามที่เรารับรู้ pitch ได้) เสียงนั้น ก็สามารถนำไปใช้สร้างทำนองเพลงได้โดยเปลี่ยนอัตราการซ้ำคาบของเสียง แต่ถ้าเสียงไม่ทำให้เกิดการรับรู้ pitch เราก็เอาเสียงนั้นไปทำเป็นทำนองเพลงไม่ได้ เช่น คุณไม่สามารถใช้เสียงที่ความถี่สูงกว่า 5 kHz หรือต่ำกว่า 25 Hz ไปสร้างทำนองเพลงได้ ก็แปลว่า เสียงในช่วง 25 Hz ถึง 5 kHz เท่านั้นที่ทำให้เกิด pitch ส่วนเสียงที่มีความถี่อยู่นอกช่วงนี้ ไม่ทำให้เกิดการรับรู้ pitch (C.J. Plack, The Sense of Hearing)
สมมติเราเอาโทน G3 (196 Hz) ผสมกับฮาร์โมนิก 4 ตัวแรก แล้วทดลองฟัง pure G3, complex tones, กับ complex tones ที่ลบ fundamental frequency ทิ้ง เราจะรับรู้ pitch เดียวกัน (หรือโน้ตดนตรี G3 ตัวเดียวกัน) ด้วยคุณภาพเสียง (หรือ timbre) ต่างกัน
รูปด้านล่างแสดง waveform กับสเปกตรัมของเสียง 3 เสียง เสียงแรก บนสุดเป็น pure tone เสียงที่สองกับสามเป็น complex tones ทั้งสามเสียงมี pitch เดียวกัน เพราะทั้งสามเสียงมีความถี่มูลฐานเดียวกัน (ความถี่มูลฐานเป็นตัวกำหนด pitch)

โค้ด MATLAB สำหรับทดลองเล่น ๆ ฟังก์ชั่น tonegen สร้างคลื่น sine ที่ความถี่ Ft Hz ยาว Td วินาที ที่ sampling rate = Fs แซมเปิ้ล/วินาที

สคริปต์ pitch_of_complex_tone เล่นเสียง pure G3 ตามด้วย complex tones ที่มี f1+f2+f3+f4+f5 แล้วตามด้วย complex tones ที่ลบ f1 และลบ f1+f2 ตามลำดับ แต่ละคลิปยาว 2 วินาที ที่ sampling rate = 16 kHz

| Create Date : 25 กรกฎาคม 2558 | | |
| Last Update : 25 กรกฎาคม 2558 20:08:24 น. |
| Counter : 1636 Pageviews. |
| |
|
| |
|
|
|
Differential Evolution
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้สรุปจาก Section ที่ 2 ของบทความ Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces (Journal of Global Optimization 11: 341-359, 1997) ของ Rainer Storn กับ Kenneth Price
Differential Evolution (DE) เป็นอีกเทคนิคหนึ่งในตระกูล evolutionary algorithm ซึ่งผู้เขียนเคยส่งเข้าประกวด ICEO ครั้งแรก (1996) แล้วประสบผลสำเร็จ บอกว่าเป็น evolutionary algorithm ที่เร็วที่สุด DE เป็น parallel direct search method ที่ใช้ D-dimentional parameter vector จำนวน NP ตัวเป็นประชากรของรุ่น G
xi,G เมื่อ i = 1, 2, ..., NP
ซึ่งเราสร้าง vector ชุดนี้ได้โดยการสุ่มให้ครอบคลุมทั้ง parameter space หรือถ้าเป็นกรณีที่มี preliminary solution อยู่แล้ว ก็อาจจะใช้คำตอบดังกล่าวเป็นตัวตั้งต้นแล้วสร้างรุ่นแรกจากการเพิ่มสมาชิกที่ค่าเบี่ยงเบนจากคำตอบนั้นกระจายแบบปกติเข้าไปให้ได้ NP ตัว
จากนั้น DE จะสร้าง parameter vector ชุดใหม่ เรียกว่า trial vector จากขั้นตอน mutation กับ crossover แล้วเปรียบเทียบ trial vector กับ target vector (ซึ่งก็คือประชากรรุ่น G นั่นแหละ) โดยใช้ greedy criterion กล่าวคือ ใครให้ค่า cost function ต่ำกว่ากัน คนนั้นก็จะไปโผล่ในรุ่น G+1 ขั้นตอนนี้เรียกว่า selection แล้วทำซ้ำ mutation, crossover, selection, mutation ... ไปจนถึงจำนวนรุ่นที่กำหนด แล้วเอาประชากรตัวที่ดีที่สุดจากรุ่นสุดท้ายเป็นคำตอบ
ดูรายละเอียดของแต่ละขั้นตอน
Mutationเราเอา target vector xi,G เมื่อ i = 1, 2, ..., NP มาสร้าง mutant vector ด้วย
ui,G+1 = xr1,G + F*(xr2,G - xr3,G)
เมื่อ index r1, r2, r3 ∈ {1, 2, ..., NP} ถูกสุ่มขึ้นมาไม่ซ้ำกันและไม่ซ้ำกับ i (เพราะฉะนั้น DE ต้องการประชากรอย่างน้อย 4 คน), F เป็นจำนวนจริงคงที่ ∈ [0,2] ตัวอย่างการสร้าง mutant vector สองมิติแสดงดังรูป

Crossoverสิ่งที่เราจะได้รับจากขั้นตอนนี้คือ D-dimentional trial vector ui,G+1 = (u1i,G+1, u2i,G+1, ..., uDi,G+1) ซึ่งสร้างจาก
uji,G+1 = vji,G+1 ถ้า randb(j) <= CR หรือ j = rnbr(i)
uji,G+1 = xji,G ถ้าไม่ใช่เงื่อนไขแรก
เมื่อ randb(j) คือ ค่าสุ่มในช่วง [0,1] ซึ่งเป็นการสุ่มแบบ uniform ของ parameter ตัวที่ j, CR คือ ค่าคงที่ crossover ∈ [0,1] เช่นกัน, และ rnbr(i) คือ การสุ่ม index ตัวหนึ่งจากเซ็ต {1, 2, ..., D} เพื่อเป็นการรับประกันว่า จะมีพารามิเตอร์อย่างน้อยหนึ่งตัวของ ui,G+1 ที่มาจาก mutant vector vi,G+1
ขั้นตอน crossover แสดงตัวอย่างกรณีที่มีพารามิเตอร์ 7 ตัวดังรูป
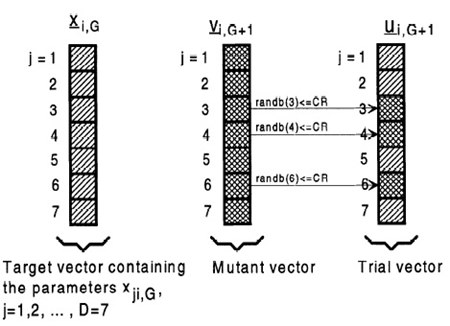
Selectionเป็นการเปรียบเทียบ trial vector ui,G+1 กับ target vector xi,G ว่าใครจะได้เป็น target vector รุ่นถัดไป xi,G+1
ใน Section ที่ 4 ของบทความพูดถึงการเลือก NP, F, CR โดยมีคำแนะนำว่า NP ระหว่าง 5*D ถึง 10*D เวิร์ก, F = 0.5 เวิร์ก, CR ให้ลองที่ 0.1 และ CR ยิ่งมากยิ่งเร็ว ดังนั้น ครั้งแรกควรเริ่มที่ CR = 0.9 หรือ 0.1 ก่อนเพื่อดูว่าคำตอบแบบเร็ว ๆ เป็นไปได้มั้ย
| Create Date : 28 มกราคม 2558 | | |
| Last Update : 28 มกราคม 2558 16:53:54 น. |
| Counter : 2702 Pageviews. |
| |
|
| |
|
|
|
The Critical Band Concept & The Power Spectrum Model
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
การทดลองคลาสสิกปี 1940 ของ Fletcher วัดขีดเริ่มการได้ยินของสัญญาณเสียงรูป sine เป็นฟังก์ชั่นของ bandwidth ของ band-pass noise ที่เป็น masker ซึ่งการทดลองได้เซ็ตให้ความถี่กลางของ noise อยู่ตรงความถี่ของสัญญาณพอดี และกำหนดให้ power density ของ noise เป็นค่าคงที่ หมายความว่า กำลังงานรวมของ noise เพิ่มมากขึ้น เมื่อ bandwidth ของมันกว้างขึ้น การทดลองถูกทำซ้ำหลายครั้ง และผลลัพธ์ที่ได้ก็แบบเดียวกัน กล่าวคือ ในตอนแรก ขีดเริ่มการได้ยินสัญญาณจะเพิ่มขึ้นตาม bandwidth ของ noise ที่เพิ่มขึ้น จนถึงจุดหนึ่ง ขึดเริ่มดังกล่าวจะมีลักษณะแบบราบ ไม่ว่า bandwidth ของ noise จะเพิ่มขึ้นเท่าไรก็ตาม ดังรูป

หมายความว่า หลังจากที่ความกว้างย่านความถี่ของ noise กว้างเกินค่าหนึ่งไปแล้ว ขีดเริ่มการได้ยินสัญญาณเสียงรูป sine ของเราจะเหมือนเดิม ถึงแม้ noise จะเสียงดังขึ้น
Fletcher อธิบายปรากฏการณ์นี้โดยอิงกับข้อเสนอของ Helmholtz ที่ว่า ระบบรับรู้เสียงของเราทำตัวเหมือนกับว่ามันมี band-pass filters จำนวนหนึ่งเรียงต่อกันเป็น bank โดยที่ย่านความถี่ passbands ของแต่ฟิลเตอร์แต่ละตัวมีส่วนเหลื่อมกัน เราเรียกฟิลเตอร์เหล่านี้ว่า 'auditory filter' ซึ่ง Fletcher คิดว่า basilar membrane เป็นต้นตอของฟิลเตอร์เหล่านี้ แต่ละตำแหน่งบนบาซิลาร์เม็มเบรนจะตอบสนองต่อช่วงของความถี่ที่จำกัด ดังนั้น จุดที่แตกต่างกันจะสัมพันธ์กับฟิลเตอร์ที่มีความถี่กลางต่างกัน
ตอนที่เราพยายามจะตรวจจับ (ฟัง) สัญญาณที่มี noise เป็นฉากหลัง เราจะใช้ฟิลเตอร์ที่มีความถี่กลางใกล้เคียงกับความถี่ของสัญญาณ โดยเจ้าฟิลเตอร์ตัวนี้จะปล่อยให้สัญญาณผ่าน และกำจัดสัญญาณรบกวนที่อยู่นอกย่านความถี่ผ่านของฟิลเตอร์ นั่นคือ เฉพาะความถี่ของสัญญาณรบกวนที่ผ่านฟิลเตอร์เท่านั้นที่จะทำให้เกิด masking effect
ทั่วไป เราจะถือว่า ขีดเริ่มการได้ยินสัญญาณ ถูกกำหนดโดยปริมาณ noise ที่ผ่านฟิลเตอร์ พูดอีกอย่างว่า ขีดเริ่มดังกล่าวสัมพันธ์กับ SNR ที่เอ้าท์พุตของฟิลเตอร์ ชุดของสมมติฐานเหล่านี้รู้จักกันในนาม 'power spectrum model' ของ masking
คำอธิบายผลลัพธ์จากการทดลองนี้คือ ตราบเท่าที่ความกว้างของ noise ยังแคบกว่า bandwidth ของฟิลเตอร์ การเพิ่ม bandwidth ของ noise ก็เท่ากับการเพิ่ม noise ที่เอ้าท์พุตของฟิลเตอร์ ทำให้ขีดเริ่มการได้ยินสัญญาณเสียงเพิ่มขึ้น จนกระทั่งความกว้างของ noise กว้างกว่า bandwidth ของฟิลเตอร์ การเพิ่มความกว้างของมันก็ไม่มีผลอะไรต่อ SNR ที่เอ้าท์พุตของฟิลเตอร์อีกต่อไป Fletcher เรียก bandwith ที่ขีดเริ่มการได้ยินหยุดเพิ่มขึ้นนี้ว่า 'critical bandwidth' (CB)
ในการวิเคราะห์ผลการทดลอง Fletcher ตั้งสมมติฐานว่า รูปร่างของ auditory filter เป็นรูปสี่เหลี่ยมมุมฉาก คำว่า critical band ที่ใช้กัน มักใช้คู่กับสมมติฐานฟิลเตอร์สี่เหลี่ยมมุมฉากอันนี้นะครับ (ทั้งนี้ก็เพื่อความง่ายในการคำนวณ อันที่จริง Fletcher ก็รู้นั่นแหละว่า ไม่ใช่) Fletcher บอกว่า เราสามารถคำนวณค่าของ CB ทางอ้อมแบบประมาณได้ โดยการวัดขีดเริ่มการได้ยินของโทนใน broadband white noise ร่วมกับสมมติฐานว่า (1) เฉพาะย่านความถี่แคบ ๆ ที่อยู่รอบ ๆ โทนซึ่งผ่านฟิลเตอร์ไปได้เท่านั้นที่ส่งผลต่อการ masking ของโทน และ (2) ขณะที่ noise ได้ mask โทนพอดีนั้น อัตราส่วนของกำลังงานของโทน (P) ต่อกำลังงานของ noise ที่อยู่ใน CB เป็นค่าคงที่ K
เรานิยมบอกกำลังงานของ noise ในรูปของกำลังงานในย่านความถี่กว้าง 1 Hz เรียกว่า noise power density เขียนแทนด้วยสัญลักษณ์ N0 และสำหรับ white noise ค่า N0 ไม่แปรตามความถี่ ฉะนั้น กำลังงานรวมของ noise ที่อยู่ใน CB กว้าง W Hz จึงเท่ากับ N0 x W
เราจึงเขียนสมการจากสมมติฐานที่ 2 ของ Fletcher ได้ว่า P/(W x N0) = K หรือ W = P/(K x N0) นั่นคือ ถ้าเรารู้ค่า N0 และวัดค่าของ P และสามารถประมาณค่า K ก็เป็นไปได้ที่จะรู้ความกว้างของ CB
Fletcher ประมาณว่า K = 1 ดังนั้น W = P/N0 (มักเรียกกันว่า critical ratio) แต่ต่อมา เรารู้ว่าค่าประมาณ K ของ Fletcher นี้ไม่ค่อยตรงนัก การทดลองหลัง ๆ บอกว่า K ประมาณ 0.4 อย่างไรก็ตาม ค่า K ขึ้นอยู่กับวิธีที่ใช้วัดขีดเริ่มการได้ยิน และแปรตามความถี่กลาง ซ้ำร้ายค่า K ของแต่ละคนก็ไม่เท่ากัน ฉะนั้น critical ratio จึงไม่ใช่ตัวบ่งชี้ที่ถูกต้องนัก
การประมาณค่า CB ในปัจจุบันอิงอยู่กับผลลัพธ์จากการทดลอง masking ซึ่งใช้ในการคำนวณ ERB ของ auditory filter นั่นคือ ERB สามารถถือว่าเป็นการวัดค่าของ CB ได้นะครับ แต่เพื่อเป็นการแยกระหว่างการวัดสมัยใหม่กับยุคเก่า การวัดแบบใหม่จึงบรรยายด้วย ERB
ที่มา: Brian C. J. Moore, An Introduction to the Psychology of Hearing (6th Ed), Emerald, 2012
| Create Date : 21 ตุลาคม 2556 | | |
| Last Update : 21 ธันวาคม 2556 3:09:26 น. |
| Counter : 1885 Pageviews. |
| |
|
| |
|
|
|
|

