|
|
Hilbert-Huang Transform
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
HHT ถูกออกแบบมาเพื่อวิเคราะห์สัญญาณ nonstationary และ nonlinearity ประกอบด้วยส่วนสำคัญ 2 ส่วน คือ empirical mode decomposition (EMD) กับ Hilbert spectral analysis (HSA) โดย HHT จะใช้วิธี EMD ในการแยกสัญญาณออกเป็น intrinsic mode function (IMF) แล้วใช้ HSA ในการหาข้อมูล instantaneous frequency (HSA คือ วิธีวิเคราะห์สัญญาณที่ใช้การแปลงฮิลแบร์ตในการคำนวณ instantaneous frequency ของสัญญาณ)
1. การแปลงฮิลแบร์ตของ x(t) คือ y(t)
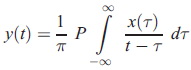
เมื่อ P คือ Cauchy principle value ของ singular integral และเราได้ analytic function z(t) = x(t) + iy(t) = a(t)eiθ(t) ค่าของ instantaneous amplitude a(t) = (x2 + y2)1/2 และ instantaneous phase θ(t) = tan-1(y/x) โดยอัตราการเปลี่ยนแปลง instantaneous phase ต่อเวลานี่แหละครับคือ instantaneous frequency ω = dθ/dt
เนื่องจากทั้ง amplitude และ frequency เป็นฟังก์ชั่นของเวลา ดังนั้นเราสามารถเขียน amplitude (หรือพลังงานซึ่งก็คือแอมปลิจูดยกกำลังสอง) ในรูปของฟังก์ชั่นของเวลาและความถี่ H(ω,t) เรานิยาม marginal spectrum จาก
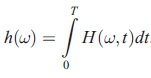
เมื่อข้อมูลดังกล่าวถูกนิยามในช่วงโดเมนเวลา [0,T] โดยค่า marginal spectrum บ่งบอกถึงแอมปลิจูด (พลังงาน) สะสมตลอดช่วงของข้อมูลในแง่ของโอกาส และยังเป็นวิธีการวัดแอมปลิจูด (หรือพลังงาน) รวมที่เป็นผลมาจากแต่ละค่าความถี่ ฉะนั้นจึงเป็นอีกทางเลือกหนึ่งในการแสดงสเปกตรัมของข้อมูลแทนการแสดงด้วยสเปกตรัมฟูริเยร์แบบเก่า
ตัวอย่าง
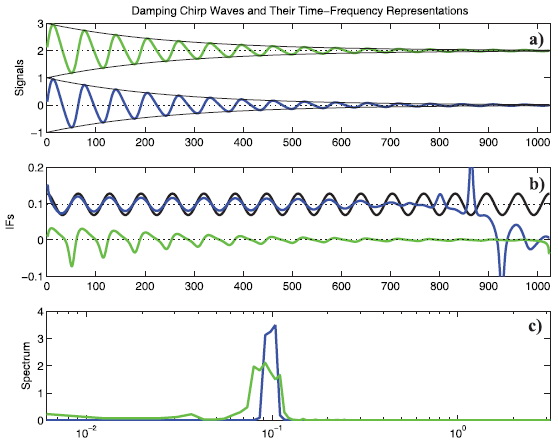
จากรูป (a) เส้นทึบสีน้ำเงินกับสีเขียวแสดง oscillatory function อย่างง่าย ตามสมการ
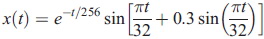
โดยเส้นสีน้ำเงินขี่บนค่าเฉลี่ย 0 ส่วนเส้นสีเขียว บนค่าเฉลี่ย 2 เส้นสีดำเล็ก ๆ เป็น upper กับ lower envelopes (b) เส้นสีดำคือ instantaneous frequency จริง ส่วนเส้นสีน้ำเงินกับเขียวคือ instantaneous frequency จากการแปลงฮิลแบร์ต (c) เส้นสีน้ำเงินแสดงสเปกตรัมฟูริเยร์ เส้นสีเขียวแสดง marginal spectrum
2. สมมติฐานของ EMD คือ ณ เวลาใด ๆ ข้อมูลอาจจะมี oscillatory modes อย่างง่ายของความถี่ที่แตกต่างกันอย่างมีนัยสำคัญอยู่ร่วมกัน ซ้อนทับกัน องค์ประกอบแต่ละตัวจะเรียกว่า IMF ซึ่งมีเงื่อนไขดังต่อไปนี้ (1) จำนวน extrema และจำนวน zero crossing ของทั้ง data set จะแตกต่างกันได้ไม่เกิน 1, (2) ณ จุดใด ๆ (data point) ค่าเฉลี่ยของ envelope ที่นิยามโดย local maxima และ local minima จะต้องเท่ากับ 0
ตัวอย่าง
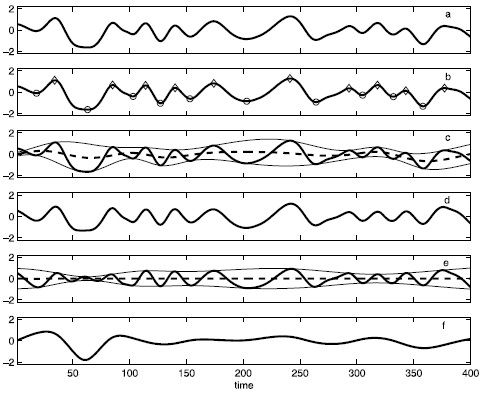
สัญญาณอินพุต x(t) คือ เส้นทึบในรูป a และ b โดยขั้นตอน sifting เริ่มด้วยการระบุ local extrema ทั้งหมด ในรูป b ใช้สัญลักษณ์ข้าวหลามตัดระบุจุด maxima และใช้สัญลักษณ์วงกลมระบุจุด minima แล้วลากเส้น cubic spline เชื่อม local maxima ทั้งหมดเข้าด้วยกันเพื่อให้ได้ upper envelope และเชื่อม local minima ด้วยเส้น cubic spline ได้ lower envelope ดังรูป c ซึ่งโดยทั่วไปข้อมูลทั้งหมดจะถูกตีกรอบด้วย 2 เส้นนี้นะครับ จากนั้น หาเส้น m1 หรือเส้นประตามรูป c เป็นเส้นที่เป็นค่าเฉลี่ยของ upper กับ lower envelope
ผลต่างระหว่างอินพุต x(t) กับ m1 คือ protomode แรก เขียนแทนด้วย h1 ดังรูป d
h1 = x(t) - m1
h1 ถือว่าเป็น proto-IMF ที่จะเอามาวนลูปทำซ้ำ h1 - m11 = h11 หลังจากทำซ้ำไป k ครั้ง h1(k-1) - m1k = h1k เราได้ h1k ที่สอดคล้องกับเงื่อนไขของการเป็น IMF (ดังรูป e, ส่วนรูป f คือผลลัพธ์จากการลบรูป a ด้วยรูป e) มันก็จะกลายเป็น IMF c1 = h1k เงื่อนไขการหยุดมีหลายแบบนะครับ เช่น ผลต่าง normalized squared ระหว่างการทำ sifting 2 รอบที่ติดกัน ซึ่งนิยามจาก
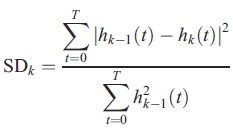
จะต้องน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าค่าหนึ่ง ตัวอย่าง SDk ที่แตกต่างอีกอัน (ซึ่งจะต้องน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าเช่นกัน) เช่น
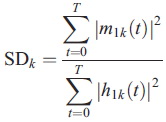
เงื่อนไขการหยุดดังกล่าว เราเรียกว่าเป็นแบบ Cauchy types นะครับ ถึงแม้จะดู rigorous ในทางคณิตศาสตร์ แต่ในทางปฏิบัติ implement ได้ยาก เพราะ ตรงที่บอกว่าน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าค่าหนึ่งนี่ คำถามคือ ค่าไหน? อีกอย่าง ผลต่างกำลังสองอาจจะมีค่าน้อย แต่มันก็ไม่ได้รับประกันว่าจำนวน zero crossing กับ extrema จะเท่ากัน Huang จึงได้เสนอเงื่อนไขการหยุดอีกแบบ เรียกว่าการหยุดแบบ S (S stoppage) ซึ่งกระบวนการ sifting จะหยุดก็ต่อเมื่อ (1) จำนวนของ zero crossing กับ extrema แตกต่างกันไม่เกิน 1 และ (2) มีค่าเท่าเดิม S รอบติดกัน ค่า S ที่ Huang เสนอคืออยู่ระหว่าง 3 ถึง 8
IMF แรกควรจะมีส่วนที่สั่นด้วยคาบสั้นที่สุด (shortest-period oscillation) ในสัญญาณ เมื่อนำไปลบออกจากสัญญาณจะได้ residue r1 = x(t) - c1 ซึ่งมีการสั้นด้วยคาบที่ยาวกว่า เราก็ใช้ residue นี่แหละครับเป็น data ใหม่ เอาไปผ่านกระบวนการ sifting เหมือนเดิมเพื่อให้ได้ IMF ของความถี่ต่ำกว่า การเอา residue ไปทำซ้ำนี้ เราจะหยุดเมื่อ rn กลายเป็น monotonic function หรือเป็นฟังก์ชั่นที่มี extremum เดียว ซึ่งไม่อาจถอด IMF ออกมาได้อีก
r1 - c2 = r2
...
rn-1 - cn = rn
ฉะนั้นเราได้
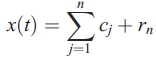
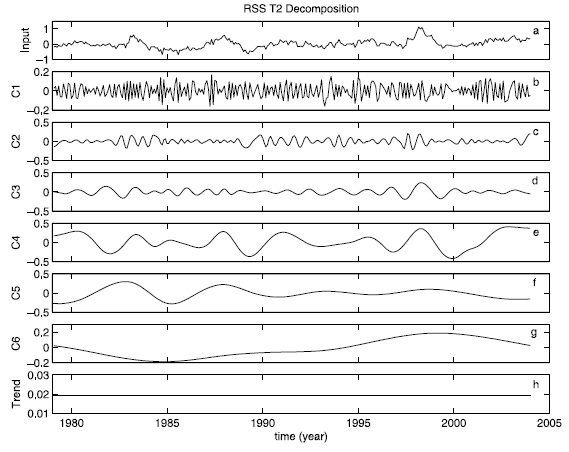
ข้อมูลต้นฉบับ x(t) แยกออกมาเป็น IMF จำนวน n ตัว และ final residue rn ตัวอย่างแสดงดังรูปด้านล่าง เป็นการแยกข้อมูลจาก Remote Sensing System (RSS) T2 ตามรูป a ออกเป็น IMF รูป b - h จากความถี่สูงไปต่ำ
ถ้า x(t) เป็น time series ความยาว N เมื่อเอามาแยกด้วย EMD และหา instantaneous frequencies กับ instantaneous amplitudes ของแต่ละ IMF เราสามารถเขียนแทน x(t) ด้วย
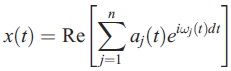
เมื่อ Re[ ] แทนส่วนจริงของพจน์ที่อยู่ใน [ ] ในที่นี้เราตัด rn ทิ้งเพราะมันเป็น monotonic function หรือเป็นฟังก์ชั่นที่มี extrema เดียวซึ่งมีข้อมูลไม่เพียงพอที่จะยืนยันว่ามันเป็น oscillatory component ความถี่ของมันมีความหมายทางกายภาพ เห็นว่าทั้งแอมปลิจูดและความถี่ของแต่ละ component ในสมการนี้เป็นฟังก์ชั่นของเวลา ซึ่งการกระจายข้อมูลแบบฟูริเยร์ของข้อมูลชุดเดียวกันนี้จะอยู่ในรูป
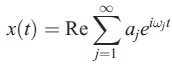
โดยที่ทั้ง aj และ ωj เป็นค่าคงที่ เมื่อเปรียบเทียบ 2 สมการ จะเห็นว่า IMF เป็นการแสดงถึงการกระจายฟูริเยร์ในกรณีทั่วไป แอมปลิจูดที่เปลี่ยนค่าได้และ instantaneous frequency ไม่เพียงพัฒนาประสิทธิภาพของการกระจาย แต่ยังทำให้การกระจายเหมาะสำหรับข้อมูลที่ไม่เป็นเชิงเส้นและเปลี่ยนแปลงแบบ nonstationary
HHT เป็นอีกทางเลือกหนึ่ง (และอาจเป็นทางเลือกที่มีความหมายทางกายภาพมากกว่า) ในการแทนข้อมูล เหตุผลคือ มันสามารถใช้ instantaneous frequency ในการบรรยาย intrawave frequency modulation นิยามของความถี่แบบปกติทั่วไปนันคือ ω = 1/T เมื่อ T คือ คาบของการสั่นใช่มั้ยครับ ถึงแม้นิยามนี้จะเป็นมาตรฐาน แต่มันก็ยังหยาบและไม่ครอบคลุม intrawave frequency modulation ซึ่งเป็นส่วนสำคัญของการสั่นแบบไม่เป็นเชิงเส้น ตัวอย่างความล้มเหลวดังกล่าวสามารถแสดงได้โดยด้วยสมการ Duffing
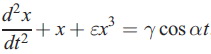
เมื่อ ε, γ และ α เป็นค่าคงที่, พจน์กำลังสามในสมการ Duffing ทำให้เกิดความไม่เป็นเชิงเส้น และเมื่อเราจัดรูปสมการใหม่
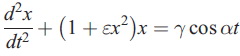
เห็นได้ชัดว่าพจน์ในวงเล็บสามารถตีความเป็นค่าคงที่สปริงที่ไม่คงที่ (a variable spring constant) หรือความยาวของลูกตุ้มที่เปลี่ยนค่าได้ (varying pendulum length) (นึกถึงสมการการเคลื่อนที่ของสปริงที่อธิบายด้วย nonhomogeneous differential) ไม่ว่าจะยังไงความถี่ก็เปลี่ยนในหนึ่งคาบ ซึ่ง intrawave frequency modulation ก็คือ harmonics ในมุมมองแบบเก่า และ Huang แย้งว่าการแสดงด้วย harmonic เป็นสิ่งที่สร้างขึ้นมาในทางคณิตศาสตร์ (a mathematical artifact) โดยมีความหมายทางกายภาพน้อยนิด ขณะที่ instantaneous frequency มีความหมายทางกายภาพมากกว่า และไม่เพียงสามารถใช้บรรยายการเปลี่ยนแปลง interwave frequency เนื่องจาก nonstationary เท่านั้น ยังใช้บรรยาย intrawave frequency modulation เนื่องจาก nonlinearity ได้ด้วย
เปรียบเทียบการวิเคราะห์ฟูริเยร์ เวฟเล็ต กับ HHT แสดงดังตาราง
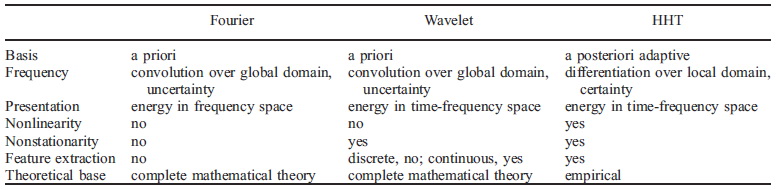
ที่มา: เก็บความจากหัวข้อ A Brief Description of HHT ใน A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies โดย Norden E. Huang กับ Zhaohua Wu
| Create Date : 16 กรกฎาคม 2556 |
| Last Update : 16 กรกฎาคม 2556 22:19:09 น. |
|
0 comments
|
| Counter : 3051 Pageviews. |
 |
|
|
|
|
|

