|
|
The Nature of Sound (สรุป)
เนื้อหาตอนนี้เรียงลำดับตามสรุปในหัวข้อ 2.6 Summary และขยายความตามเนื้อหาในหัวข้อก่อนหน้าจากบทที่ 2 The Nature of Sound หนังสือ The Sense of HEARING ของ Christopher J. Plack
1. เสียงเกิดจากการเปลี่ยนแปลงความดันในตัวกลางบางอย่าง เช่น อากาศ ความดันที่เปลี่ยนแปลงนี้จะกระจายออกจากแหล่งกำเนิดเสียงด้วยอัตราเร็วที่ขึ้นอยู่กับชนิดของตัวกลางนั้น เช่น อัตราเร็วเสียงในอากาศที่ความดันบรรยากาศ มีค่าประมาณ 330 เมตร/วินาที (อัตราเร็วเสียงในอากาศ นอกจากจะขึ้นกับความดันอากาศแล้วยังขึ้นอยู่กับอุณหภูมิอีกด้วย) โมเดลการสั่นหรือการเปลี่ยนแปลงความดันของตัวกลางสามารถแสดงได้ด้วยสายโซ่ลูกกอล์ฟที่เชื่อมกันด้วยสปริง รูปแสดงเฟรมเวลา 6 เฟรมต่อเนื่องกันจากบนลงล่าง
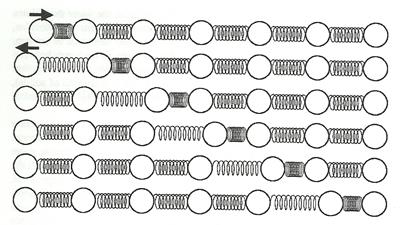
การทำให้ความดันเปลี่ยนแปลงจุดใดจุดหนึ่ง จะส่งผลให้การเปลี่ยนความดันนั้นแพร่กระจายตัวออกด้วยอัตราเร็วที่ขึ้นอยู่กับความหนาแน่น (density) และความแข็งทื่อ (stiffness) ของสสารตัวกลาง ถ้าตัวกลางหนาแน่นมาก อัตราเร็วจะต่ำ เพราะวัตถุที่มวลมากใช้เวลานานกว่าในการเร่ง ส่วนตัวกลางที่แข็งทื่อกว่า อัตราเร็วเสียงจะมากกว่า เช่น เสียงเดินทางในเหล็ก (stiffness สูงมาก) ด้วยอัตราเร็ว 5200 m/s ขณะที่เดินทางในยางวัลกาไนซ์ (vulcanized rubber) ซึ่งมีความหนาแน่นสูงแต่ไม่แข็งทื่อ ด้วยอัตราเร็ว 54 m/s กรณีตัวกลางคือน้ำ ถึงแม้น้ำจะหนาแน่นกว่าอากาศ แต่ stiffness ของน้ำสูงกว่าอากาศมาก ทำให้อัตราเร็วของเสียงในน้ำประมาณ 1500 m/s
2. pure tone คือ เสียงที่มีการเปลี่ยนแปลงความดันเมื่อเวลาผ่านไปแบบ sinusoidal โดยความถี่ของ pure tone หาได้จากจำนวนลูกคลื่น (การสลับกันหนึ่งรอบของสันคลื่นกับท้องคลื่น) ที่เกิดขึ้นในช่วงเวลา และคาบของ pure tone คือ เวลาระหว่างยอดคลื่นสองยอดที่อยู่ติดกัน ระยะห่างระหว่างยอดคลื่นทั้งสองนั้น เรียกว่า ความยาวคลื่น
3. ขนาด (magnitude) ของคลื่นเสียงสามารถพูดถึงได้ในรูปของ ความดัน หรือความเข้ม (intensity) ของคลื่นเสียง หรือพูดถึงระดับเสียงในหน่วย logarithm ที่เรียกว่า เดซิเบล (dB) เรานิยมใช้หน่วย dB เพราะหากใช้หน่วยของความดัน (N/m2) หรือความเข้ม (W/m2) นั้น ช่วงความกว้างของเสียงที่เราได้ยินจะมีค่ามหาศาล ไม่สะดวก พูดไปพูดมาแล้วงง เสียงที่เริ่มทำให้เราเจ็บปวดมีขีดเริ่มที่ความเข้มประมาณ 1,000,000,000,000 เท่าของความเข้มเสียงเบาที่สุดที่เราได้ยิน
ระดับเสียงในหน่วย dB = 10 log10(I/I0) หรือ = 20 log10(P/P0) เพราะ I ∼ P2
I0 และ P0 คือ ระดับความเข้มอ้างอิงและความดันอ้างอิง ว่ากันตามความนิยมนั้น สำหรับระดับเสียงในอากาศ เราใช้ความดันอ้างอิงเท่ากับ 0.00002 N/m2 (หรือ I0 = 10-12 W/m2) และถ้าใช้ความดันอ้างอิงค่านี้ เราจะเรียกระดับเสียงในหน่วย dB ดังกล่าวว่า SPL (sound presure level) นั่นคือ เสียงที่มีความดันเท่ากับความดันอ้างอิง จะมีระดับเสียงเท่ากับ 0 dB SPL (ตามนิยาม เพราะ P = P0 และ log 1 = 0) อันที่จริงค่าความดันอ้างอิงดังกล่าว เราเลือกเพราะ 0 dB SPL จะมีค่าใกล้เคียงกับระดับเสียงต่ำที่สุดที่เราสามารถได้ยินที่ความถี่ 1 kHz
ลองคิดเล่น ๆ ครับ ความดันบรรยากาศประมาณ 105 N/m2 และเสียงเบาสุดที่เราสามารถได้ยินสัมพันธ์กับความผันผวนของความดันราว 2 x 10-5 N/m2 หมายความว่า เราสามารถได้ยินคลื่นเสียงที่มีความดันผันผวนต่ำกว่าหนึ่งในพันล้านของความดันบรรยากาศ เปรียบเทียบได้กับคลื่นน้ำที่มีความสูงแค่ 1 มิลลิเมตรบนผิวมหาสมุทรที่มีความลึก 1,000 กิโลเมตร !!! แม้กระทั่งเสียงที่ระดับ 120 dB SPL อันเป็นระดับที่ทำให้คุณปวดหูและส่งผลเสียต่อหู ก็มีความผันผวนของความดันด้วยขนาดที่ต่ำกว่าระดับความดันบรรยากาศถึงห้าพันเท่า กำลังจะบอกว่า การเปลี่ยนแปลงของความดันคลื่นเสียงที่เราได้ยินกันในชีวิตประจำวันนั้นมีค่าน้อยนิดเพียงไร แสดงให้เห็นว่าหูของเราเป็นอวัยวะที่ sensitive เพียงไร
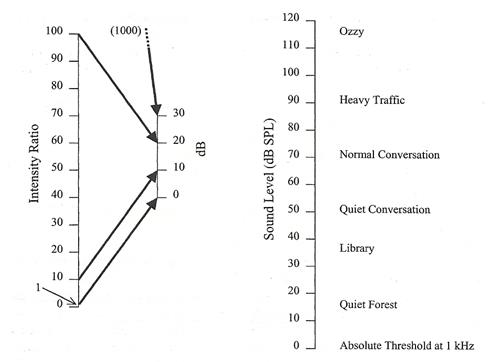
รูปแสดงการจับคู่ (map) ระหว่างอัตราส่วนของความเข้ม I/I0 กับ dB SPL และแสดง dB SPL ของเสียงต่าง ๆ ในชีวิตประจำวัน ที่ระดับสูงสุด ผู้เขียนใช้คำว่า Ozzy นั้นอ้างถึง Ozzy Osbourne ร็อกเกอร์ในตำนาน เป็นความกวนและขี้เล่นของผู้เขียนครับ แกบอกว่า ครั้งหนึ่งเคยได้ยิน Ozzy Osbourne บอกว่า เดี๋ยวนี้เขาไม่ค่อยได้ยินเสียงอะไรเท่าไร เพราะที่ผ่านมาฟังเสียงดัง 30 พันล้านเดซิเบลมาทั้งชีวิต ซึ่งระดับ 30 พันล้านเดซิเบลนั้นเท่ากับ 102999999988 W/m2 อันเป็นกำลังงานที่มากพอจะทำลายทั้งเอกภพ นับประสาอะไรกับหูของ Ozzy จึงเขียนในกราฟด้านบนที่ระดับสูงสุดไว้ว่า Ozzy
อย่าลืมว่าหน่วย dB เป็นสเกล logarithm นะครับ ถ้าเรารวมเสียงระดับ 40 dB SPL เข้ากับอีกเสียงหนึ่งซึ่งมีระดับ 40 dB SPL เหมือนกัน ผลลัพธ์ที่ได้จะไม่ใช่เสียงที่มีระดับ 80 dB SPL เพราะเสียง 80 dB SPL นั้นมีความเข้มมากกว่าเสียง 40 dB SPL ถึงหนึ่งหมื่นเท่า (เพราะ 40 dB ⇔ I = 10,000 I0 และ 80 dB ⇔ I = 100,000,000 I0) ในความเป็นจริง สองเสียงนี้รวมกันจะได้เสียงที่ระดับ 43 dB SPL (ถือว่ามีความสัมพันธ์ของเฟสเป็นแบบสุ่ม)
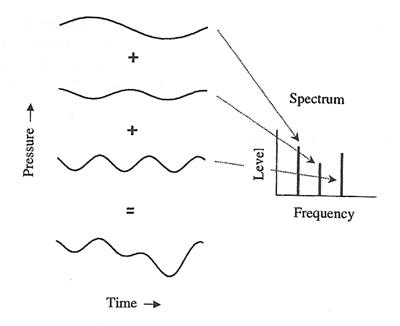
4. (4.1) คลื่นเสียงใด ๆ สามารถสร้างขึ้นได้โดยการรวม pure tone หลาย ๆ อันที่มีขนาด (amplitude) ความถี่ และเฟส ต่างกัน, (4.2) การพล็อตสเปกตรัมของคลื่นเสียงแสดงให้เห็นระดับขององค์ประกอบ pure tone แต่ละอันโดยมีโดเมนคือความถี่, (4.3) สเปกโทรแกรมของเสียงแสดง short-term spectrum ของเสียง เป็นฟังก์ชั่นของเวลา, (4.4) เนื่องจาก time-frequency tradeoff การเพิ่มความละเอียด (resolution) ในโดเมนเวลา จะลดความละเอียดในโดเมนความถี่ และการเพิ่มความละเอียดในโดเมนความถี่ จะละความละเอียดในโดเมนเวลา
รูปด้านล่างนี้แสดงตัวอย่างจากข้อความ 4.1 และ 4.2
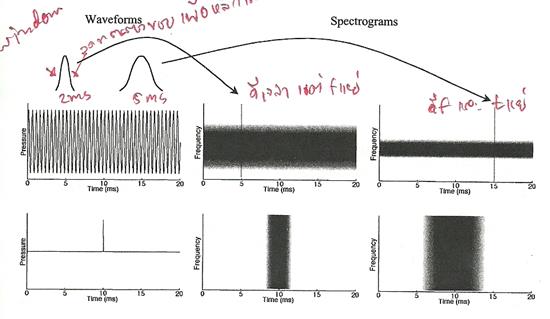
รูปต่อไปนี้แสดง waveform และสเปกตรัมของ pure tone ที่มีความถี่ 2 kHz ในช่วงเวลา 20 ms (รูปบน), 10 ms (รูปกลาง) และรูปล่างแสดง waveform กับสเปกตรัมของสัญญาณ impulse
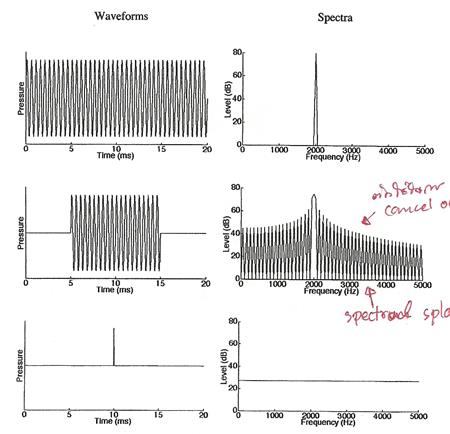
ในกรณีของ pure tone ที่ต่อเนื่องไม่มีจุดเริ่มต้น ไม่มีจุดจบนั้น สเปกตรัมของมันจะเป็นเส้นหนึ่งเส้นที่ความถี่ของ pure tone แต่ถ้าเป็น pure tone ช่วงเวลาสั้น ๆ ตามรูป สเปกตรัมของมันจะกว้างขึ้น กฎทั่วไปคือ การเปลี่ยนแปลงแอมปลิจูดทันทีทันใดในโดเมนความถี่ หมายถึงหรือสัมพันธ์กับการมีแอมปลิจูดกระจายอยู่กว้างในโดเมนเวลา และการเปลี่ยนแปลงทันทีทันใดของแอมปลิจูดในโดเมนเวลา หมายถึงการมีแอมปลิจูดกระจายอยู่กว้างในโดเมนความถี่
ความสัมพันธ์อันนี้บอกเราว่า ถ้าเราวิเคราะห์สัญญาณเสียงช่วงเวลาสั้น ๆ เท่าไร สเปกตรัมในโดเมนความถี่ของมันก็จะยิ่งกระจายออกมาก (blurred) เท่านั้น จึงเกิด time-frequency tradeoff ยิ่งความละเอียดในเวลาสูง ความละเอียดในความถี่ก็ยิ่งแย่
รูปด้านล่างแสดงสเปกโทรแกรมของสัญญาณ pure tone ต่อเนื่องและสัญญาณ impulse สเปกโทรแกรมเป็นการพล็อตระดับด้วยความเข้มของสีดำบนโดเมนเวลา (แกนนอน) และความถี่ (แกนตั้ง) หรือพูดว่าแสดง short-term spectrum ของเสียงในโดเมนเวลา จากรูป เห็นว่าถ้าช่วงของ window แคบ (ความละเอียดทางเวลาสูง) สเปกตรัมความถี่จะแผ่กว้างกว่า เบลอกว่า (เราใช้ window เพราะไม่อยากให้บริเวณขอบของการตัดนั้นเกิดการเปลี่ยนแปลงทันทีทันใด)
5. complex tone แบบซ้ำคาบจะมี waveform ที่ซ้ำ ๆ กันตลอดช่วงเวลา สเปกตรัมของเสียงเหล่านี้มีองค์ประกอบ pure tone จำนวนหนึ่ง ซึ่งมีความถี่เป็นจำนวนเต็มเท่าของความถี่มูลฐาน (fundamental frequency) หรือจำนวนของ waveform ที่เกิดขึ้นซ้ำ ๆ นั้นในหนึ่งวินาที รูปด้านล่างแสดง waveform และสเปกตรัมของ complex tone สามสัญญาณ รูปบน คาบของ waveform เท่ากับ 10 ms นั่นคือ ความถี่มูลฐานเท่ากับ 100 Hz รูปกลางกับรูปล่างมีคาบเท่ากับ 5 ms และความถี่มูลฐาน 200 Hz
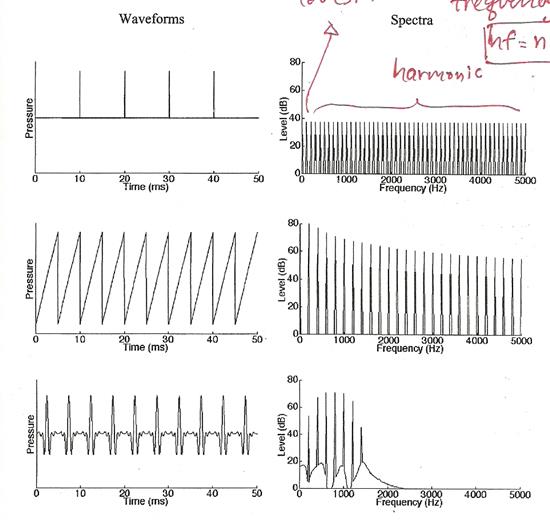
ในกรณีกลุ่มของฮาร์มอนิกส์ที่ผสมกันแบบตามใจฉัน ความถี่มูลฐานคือจำนวนที่มีค่ามากที่สุดที่สามารถเอาไปหารความถี่ของฮาร์มอนิกส์ทุกตัวได้ลงตัว เช่น ฮาร์มอนิกส์ประกอบด้วย 550 600 700 750 Hz ความถี่มูลฐานจะเท่ากับ 50 Hz
รูปด้านล่างแสดงตัวอย่าง complex tone ที่สร้างจาก pure tone หลาย ๆ ตัวซึ่งมีความถี่เป็นจำนวนเต็มเท่ารวมกัน waveform ที่เขียนเลข 1 คือองค์ประกอบมูลฐาน และจะเห็นว่าอัตราการซ้ำของ complex tone เท่ากับความถี่ขององค์ประกอบมูลฐาน คือ 200 Hz
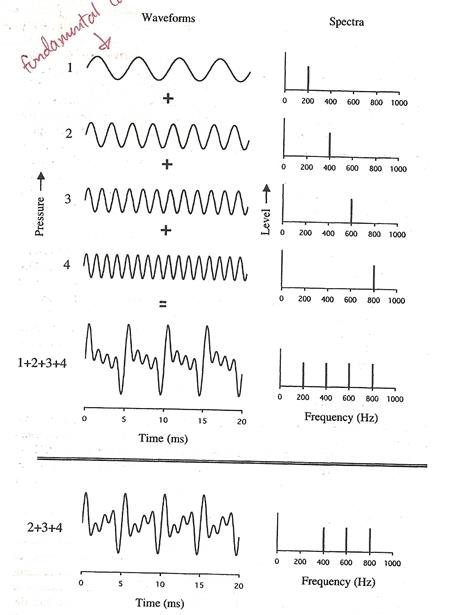
ทีนี้ สังเกตรูปล่างสุด (จากรูปข้างบน) 2+3+4 เราลบองค์ประกอบพื้นฐานทิ้งไป waveform ของมันมีหนาตาแตกต่างจาก 1+2+3+4 แต่อัตราการซ้ำรูปยังเหมือนเดิม คือ 200 Hz นั่นคือ ความถี่มูลฐานของ complex tone ขึ้นอยู่กับระยะห่างของฮาร์มอนิกส์ ไม่ใช่ความถี่ของฮาร์มอนิกส์ต่ำสุดที่ปรากฏ
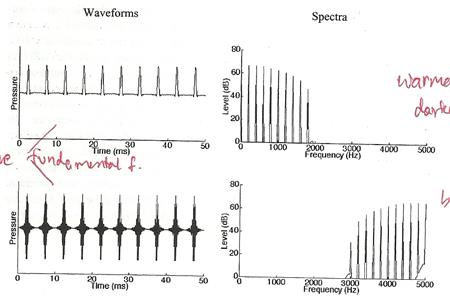
รูปด้านล่างแสดง complex tone สองเสียงที่มีความถี่มูลฐานเดียวกัน คือ 200 Hz แต่สเปกตรัมของพวกมันแตกต่างกันอย่างสิ้นเชิง เสียงรูปบนจะให้อารมณ์มืดกว่า ขณะที่เสียงจากรูปล่างจะสว่างสดใสกว่า นี่ใช้ตอบคำถามได้ว่าเหตุใดเครื่องดนตรี 2 ชิ้นที่เล่นโน้ตเดียวกันจึงมีเสียงแตกต่างกัน และให้อารมณ์แตกต่างกัน นั่นก็เพราะโครงสร้างฮาร์มอนิกของเสียงทั้งสองต่างกัน
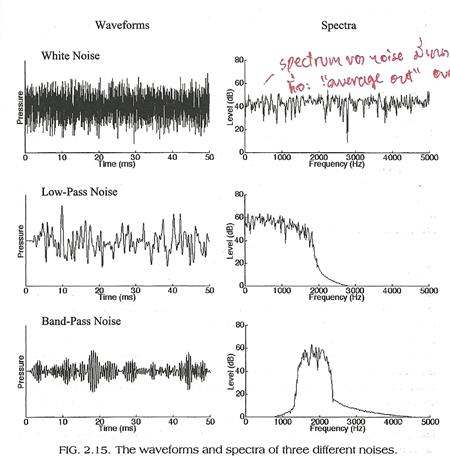
6. เสียงรบกวน (noise) มีความผันผวนของแรงดันเป็นแบบสุ่มตลอดช่วงเวลา สเปกตรัมของ noise จะมีการกระจายขององค์ประกอบทางความถี่ที่ต่อเนื่อง ตัวอย่าง noise และสเปกตรัมของมันแสดงดังรูปข้างล่างนี้
7. Amplitude modulation คือการเปลี่ยนแอมปลิจูดของ envelope ของเสียงในโดเมนเวลา, Frequency modulation คือการเปลี่ยนแปลงความถี่ของเสียงในโดเมนเวลา การดำเนินการทั้งคู่จะส่งผลกระทบต่อสเปกตรัม และสร้างองค์ประกอบทางความถี่เพิ่มเติมขึ้นมาอีกจำนวนหนึ่ง
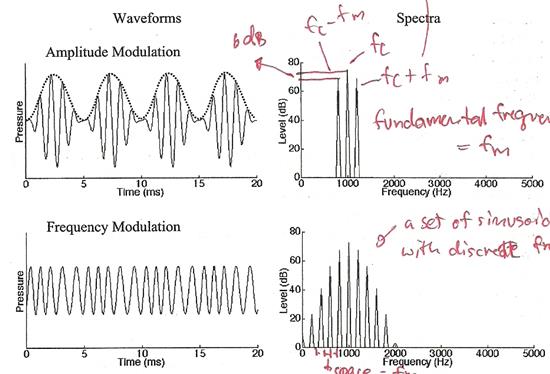
รูปบนแสดง pure tone ที่ความถี่ 1 kHz มอดูเลตแอมปลิจูดกับ sinusoidal ที่ความถี่ 200 Hz เห็นว่าสเปกตรัมมีการเปลี่ยนแปลง มี spectral side bands ที่ความถี่ 800 และ 1200 Hz ส่วนรูปล่างเป็น frequency modulation และมีระยะห่างระหว่างสเปกตรัมเท่ากับ 200 Hz
| Create Date : 25 เมษายน 2556 |
| Last Update : 26 เมษายน 2556 20:57:10 น. |
|
0 comments
|
| Counter : 5071 Pageviews. |
 |
|
|
|
|
|

