Experiments with and Enhancements to Echo Hiding
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ Sameer Mitra กับ Sathiamoorthy Manoharan ใน 4th International Conference on Systems and Networks Communication ปี 2009
INTRODUCTIONผู้เขียนแนะนำระบบ steganography โดยแบ่งเป็นฝั่งซ่อนข้อมูล (Hiding message) กับฝั่งดึงข้อมูลที่ซ่อนอยู่ออกมา (Extracting message) ดังรูป
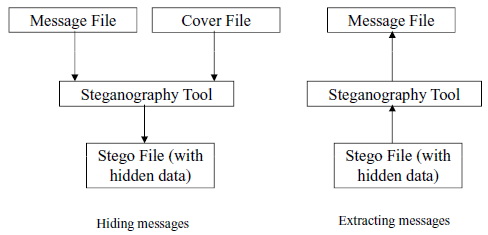
เทคนิคที่พูดถึงในบทนำมีเพียง 2 เทคนิคคือ LSB steganography กับ Echo hiding โดยในส่วนของเทคนิค LSB ได้ยกตัวอย่าง LSB แบบง่ายที่สุด คือ เปลี่ยนบิตสุดท้าย (LSB) ตามข้อมูลที่จะซ่อน สมมติว่าเราจะซ่อนตัวอักษร C (รหัส ASCII ของมันคือ 0x43 หรือ 01000011 ฐาน 2) ลงในแซมเปิ้ลของเสียงต้นฉบับ 8 แซมเปิ้ล ที่แต่ละแซมเปิ้ลมี 8 บิต ได้แก่ 11010010, 01001010, 10010111, 10001100, 00010101, 01010111, 00100110 กับ 01000011 เราก็เปลี่ยน LSBs ของทั้ง 8 แซมเปิ้ลเรียงตามค่าของ C ทีละบิต ผลลัพธ์ที่ได้ คือ 11010010, 01001011, 10010110, 10001100, 00010101, 01010110, 00100111 กับ 01000011 ตัวขีดเส้นใต้คือตัวที่เปลี่ยนแปลง (โดยเฉลี่ยแล้ว ครึ่งหนึ่งของ LSBs จะเปลี่ยนแปลง) หูของมนุษย์สามารถตรวจจับความต่างระหว่างเสียงต้นฉบับกับเสียงที่ซ่อน C ลงไปแล้วนี้ได้ค่อนข้างยาก ข้อเสียที่ชัดเจนของเทคนิค LSB คือ มันอ่อนไหวต่อการดำเนินการประมวลผลสัญญาณต่าง ๆ เช่น re-sampling, filtering, lossy data transformation ทำให้เราสูญเสียข้อมูลที่ฝังโดยการเปลี่ยน LSB ไป
เทคนิค Echo จะอ่อนไหวต่อการดำเนินการแบบดังกล่าวไม่มากเท่า LSB, แต่กระนั้น ถ้าไม่มีการดำเนินการใด ๆ เลยกับสัญญาณเสียงที่ฝังข้อมูลเรียบร้อยแล้ว หรือพูดอีกอย่างว่า อยู่ในสภาพแวดล้อมแบบ closed loop เทคนิค LSB จะสามารถดึงข้อมูลออกมาได้ 100% ขณะที่เทคนิค Echo มี recovery rate ที่ต่ำกว่า 100%
จุดประสงค์ของบทความนี้นอกจากจะทดลองเพื่อดูธรรมชาติของเทคนิค Echo แล้ว ผู้เขียนยังบอกว่าเพื่อหาวิธีเพิ่ม recovery rate โดยการใช้ชุดรหัสแบบ self-synchronizing ที่เรียกว่า T-code ซึ่งก็แน่นอนนะครับว่าการเพิ่ม recovery rate มีความหมายเดียวกับการเพิ่ม robustness ของเทคนิค Echo hiding
ECHO HIDING & RELATED WORK[สำหรับความรู้พื้นฐานดู Echo Data Hiding] ถ้า x[n] เป็นค่าแซมเปิ้ลของสัญญาณต้นฉบับ, α เป็น echo decay rate โดยที่ 0 < α < 1, และ γ คือ echo delay ซึ่งเราจะใช้ค่า delay สองค่า จะใช้ค่าไหนขึ้นอยู่กับว่าข้อมูลที่เอามาซ่อนเป็น 0 หรือ 1
เราสามารถปรับพารามิเตอร์ α กับ γ ได้เพื่อให้คนฟังไม่ได้ยิน echo และมี recovery rate ที่โอเค
กรณีเทคนิค Echo hiding แบบเบสิก ค่าของแซมเปิ้ลหลังจากใส่ echo หรือ y[n] = x[n] + αx[n - γ] รูปต่อไปนี้แสดงตัวอย่าง original segment (เซ็ตของ x[n]) ซ้าย กับ encoded segment (เซ็ตของ y[n]) ขวา ตามลำดับ
ถ้า γ ลดลง จะทำให้สัญญาณต้นฉบับกับ echo ผสมกัน ถึงจุดหนึ่ง (ประมาณ 1 ms) หูคนเราก็แยกสองสัญญาณนี้ไม่ออก ส่วน α จะเป็นตัวกำหนดแอมปลิจูดของ echo ซึ่งบางที มันก็เป็นไปได้ว่าแอมปลิจูดของ echo จะสูงกว่าค่าสูงสุดที่ยอมรับได้ กรณีก็จะต้องใช้ scaling factor เพื่อลดแอมปลิจูดของแซมเปิ้ลทั้ง segment
ในการดึงข้อมูลออกมา เราใช้ auto-correlation c[n] ของ cepstrum: c[n] = F-1(log((F(x))2))
เมื่อ x คือ สัญญาณที่ซ่อนข้อมูลลงไปแล้ว, F(x) คือ การแปลง Fourier ของ x, F-1 คือ การแปลง Fourier ผกผัน ตัวอย่าง auto-correlation ของสัญญาณแสดงดังรูป
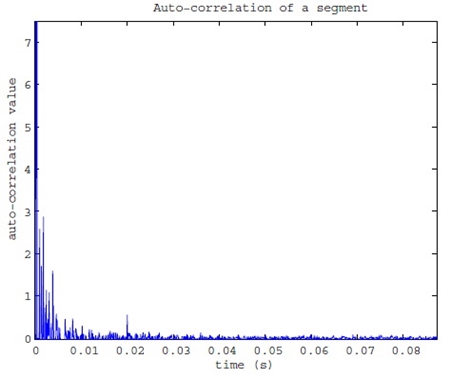
spike หรือ อิมพัลซ์ที่โดดสูงออกมาหลังจากอิมพัลซ์อันแรก ๆ ถ้าไม่อยู่ที่ γ0 ก็ต้องอยู่ที่ γ1 วินาที หลักในการดูว่าข้อมูลที่ซ่อนอยู่เป็น 0 หรือ 1 คือให้ดู spikes ที่ γ0 กับ γ1 ว่าอันไหนมีขนาดใหญ่กว่ากัน รูปที่เห็นนี้เป็นตัวอย่างที่มี echo delay γ0 = 0.01 วินาที และ γ1 = 0.02 วินาที เราเห็นว่า spike ที่ 0.02 วินาทีใหญ่กว่าที่ 0.01 วินาที ฉะนั้น segment ดังกล่าวย่อมต้องซ่อน 1 เอาไว้
Oh และคณะพัฒนาเทคนิค echo hiding นี้โดยใช้ dual echo kernel กล่าวคือมี echo สองลูก ลูกหนึ่งเป็นบวก อีกลูกเป็นลบ
y[n] = x[n] + α1x[n - γ1] - α2x[n - γ2]
โดยทั่วไป |γ1 - γ2| ≤ 5 และถึงแม้ dual kernel นี้จะพัฒนาขึ้นจาก single kernel แบบแรกที่กล่าวถึง แต่การตรวจจับ cepstrum ก็ยังไม่น่าพอใจ ต่อมา Kim และคณะจึงได้เสนอ Backward & Forward kernel ซึ่งเพิ่ม recovery rate สูงกว่าเดิม
y[n] = x[n] + αx[n - γ] - αx[n + γ]
ขีดจำกัดหลักของเทคนิค echo hiding คือ มันเป็นการยากที่จะซ่อนข้อมูลในส่วนที่เงียบของเสียง เพราะเราจะได้ยิน echo ตอนที่ไม่มีเสียง จึงได้มีการพัฒนา adaptive echo hiding กล่าวคือ มีการเปลี่ยนแปลงค่า decay rate ให้เหมาะสมกับแต่ละ segment ในการกำหนดค่าสูงสุดของ decay rate ให้แต่ละ segment นั้น เราเริ่มจากการคำนวณพลังงานสัญญาณของ segment ตามสูตร
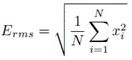
ค่าพลังงานนี้จะถูกนำไปเปรียบเทียบกับ threshold โดยเราจะซ่อนข้อมูลลงใน segment ที่มีพลังงานสูงกว่า threshold เท่านั้น แล้วจึงทำ gain control เพื่อปรับค่า decay rate เพื่อทำให้ echoes อยู่ต่ำกว่า mask (เพราะเราไม่อยากให้ใครได้ยิน echo) ผู้เขียนบอกว่าในการคำนวณ mask จะใช้วิธีใดวิธีหนึ่งใน 3 วิธีต่อไปนี้ (1.) Signal Dependent Attenuation: กรณีนี้ mask ก็คือ original host signal หรือสัญญาณต้นฉบับ และแต่ละ segment จะปรับ decay rate ในแบบที่ทำให้ echoes เกือบทั้งหมดอยู่ต่ำกว่าสัญญาณต้นฉบับ, (2.) Psychoacoustic Model: mask ก็คำนวณในโดเมนความถี่สำหรับ 26 critical bands ตามโมเดลของมันนั่นแหละครับ แล้วแต่ละ segment จะปรับค่า decay rate ในแบบที่ทำให้องค์ประกอบความถี่ของ echo ในย่าน 1 kHz ถึง 5 kHz อยู่ต่ำกว่า mask, (3.) Perceptual Filter: maks ถูกคำนวณในโดเมนเวลาโดยใช้ perceptual filter ที่อิงอยู่กับ LPC (Linear Predictive Coding) ซึ่งทำได้โดยป้อนสัญญาณต้นฉบับเข้าไปยัง perceptual weighting filter
ในกรณี adaptive นี้ ข้อมูลตำแหน่งที่ทำลายน้ำ (ข้อมูลว่า segment ไหนที่มีการฝังข้อมูลลายน้ำลงไป) จะต้องถูกบันทึกไว้ใช้ตอนทำ recovery
T-CODEST-code คือ เซ็ตย่อยของเซ็ต Huffman code ทั้งหมดที่เป็นไปได้ วิธีการสร้าง T-code เราใช้กระบวนการที่เรียกว่า T-augmentation เริ่มจากเซ็ตของ T-code อย่างง่ายที่มีแต่ alphabets ในกรณี binary alphabet เซ็ตดังกล่าวก็คือ S = {0, 1} ถ้าต้องการ code set ที่ใหญ่ขึ้น เราก็ใช้วิธีต่อไปนี้แล้วทำซ้ำไปเรื่อย ๆ ครับ คือ (1.) ลบสมาชิกหนึ่งตัวออกจากเซ็ต (2.) ใช้สมาชิกตัวที่ลบออกจากเซ็ตเป็น prefix กับสมาชิกของเซ็ตตอนเริ่มต้น เพื่อใช้เป็นสมาชิกตัวใหม่ที่เพิ่มเข้ามาของเซ็ต
ตัวอย่าง จาก S = {0, 1} ถ้าเราเลือก 0 เป็น prefix เราก็จะได้ S(0) = {1, 00, 01} ระดับถัดมา ถ้าเราเลือก 1 เป็น prefix เราก็จะได้ S(0,1) = {00, 01, 11, 100, 101} แต่ถ้าในระดับเดียวกันนี้ เราเลือก 01 เป็น prefix ก็จะได้ S(0,01) = {1, 00, 011, 0100, 0101} ซึ่งก็ชัดเจนว่า เวลาเลือก prefix ควรเลือกตัว code word ที่สั้น ๆ เพราะว่า codes ใน code set สุดท้ายจะได้สั้น ๆ
จำนวนสมาชิกในเซ็ต T-code ที่ระดับ T-augmentation เท่ากับ n คือ 2n + 1
ข้อดีของ T-code คือมันจะทำ self-synchronize ระหว่างการ decode ดังนั้น เมื่อบางบิตเกิดมีปัญหาขึ้นมาใน stream ที่เข้ารหัสแบบ T-code ตัวถอดรหัสจะทำ syncronize ใหม่อัตโนมัติ ดูตัวอย่างนะครับ สมมติว่าเราจะส่งข้อความ helloworld! ซึ่งใช้ตัวอักษร 8 ตัว คือ {h, e, l, o, w, r, d, !} ที่แต่ละตัวมีความถี่ {1, 1, 3, 2, 1, 1, 1, 1} ตามลำดับ เราต้องใช้เซ็ต T-code ที่ T-augmentation ระดับ 3 (เพราะระดับ 2 มีตัวอักษรให้ใช้แค่ 5 ตัว ซึ่งไม่พอ) คือเซ็ต S(0,1,00) = {01, 11, 100, 101, 0000, 0001, 00100, 00101} แล้วเอาไปสร้างพจนานุกรมดังตาราง
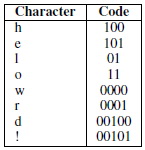
เราได้ helloworld! = 100.101.01.01.11.0000.11.0001.01.00100.00101 และโดยทั่วไป ความผิดพลาดจะเกิดขึ้นได้ 3 แบบ คือ บางบิตหายไป (bit loss), บางบิตเปลี่ยนค่า (bit inversion) และบางบิตเกินเข้ามา (bit addition)
1. Bit loss: สมมติว่าบิตที่ขีดเส้นใต้หายไป 100.101.01.01.11.0000.11.0001.01.00100.00101 ฉะนั้นบิตสตรีมใหม่จะเป็น 10010101011100001001010010000101 และตัว decoder จะถอดรหัสเป็น 100.101.01.01.11.0000.100.101.00100.00101 = hellowhed! (หมายเหตุ: ตัวอย่างนี้ไม่ตรงกับในเปเปอร์นะครับ เพราะตอนพิมพ์ผมตาลายไปขีดเส้นใต้ผิดที่ เลยตามน้ำ ถอดรหัสตามที่ขีดผิดที่นั่นแหละ)
2. Bit inversion: สมมติว่าบิตที่ขีดเส้นใต้เปลี่ยนค่า จาก 100.101.01.01.11.0000.11.0001.01.00100.00101 เป็น 1001010101110001100001010010000101 ตัวถอดรหัสจะถอดเป็น 100.101.01.01.11.0001.100.00101.00100.00101 = hellorh!d!
3. Bit addition: สมมติว่าตัวที่ขีดเส้นใต้คือบิตที่เพิ่มเข้ามา 100.11101.01.01.11.0000.11.0001.01.00100.00101 หรือ 100111010101110000110001010010000101 ตัวถอดรหัสก็จะอ่านได้ว่า 100.11.101.01.01.11.0000.11.0001.01.00100.00101 = hlelloworld!
ผู้เขียนจะใช้ T-code เพื่อเข้ารหัสข้อมูลก่อนจะฝังลงในเพลง ทางฝั่งรับก็ต้องถอดรหัส T-code ก่อนใช้งาน นอกจากนี้ พจนานุกรมที่ใช้เข้ารหัสจะต้องเป็นที่รู้กันทั้งสองฝ่าย
EVALUATIONผู้เขียนใช้เพลงที่มีลักษณะดังนี้ 8 บิต/แซมเปิ้ล, 44 kHz ช่องเดียว WAV file และข้อความที่ซ่อนคือ "Hello World!" เพลงที่ใช้มีความยาว 60 วินาที ถูกแบ่งเป็น segment ท่อนละ 0.25 วินาที ทำให้สามารถซ่อนข้อมูลได้สูงสุด 60/0.25 = 240 บิต เพลงและชนิดของเพลงที่ใช้ทดสอบแสดงดังตาราง โดยเพลงร็อกกับป๊อปจะมีพลังงานสัญญาณสูง ขณะที่เพลงบรรเลงหรือคลาสสิกจะมีปริมาณกลาง ๆ ส่วนเสียงพูดซึ่งมีช่วงว่างมากจะมีพลังงานต่ำสุด
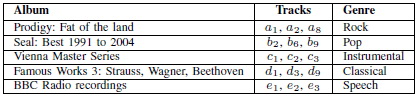
ในการวัด recovery rate จะใช้ค่าของ Bit Recovery Rate (BRR) ซึ่งหมายถึง สัดส่วนของบิตที่สามารถอ่านได้อย่างถูกต้อง กับ Character Recovery Rate (CRR) ซึ่งหมายถึง สัดส่วนของตัวอักษรที่อ่านได้อย่างถูกต้อง ผู้เขียนเริ่มการทดลองแรกด้วยการดูว่าชนิดของเพลงมีผลต่อ RR หรือไม่ โดยกำหนด α = 0.8, γ0 = 0.001 และ γ1 = 0.0012 ผลที่ได้ดังตาราง
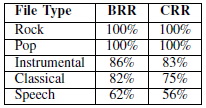
เห็นว่าเสียงที่มีช่วงเงียบมากหรือพลังงานต่ำจะมี RR ต่ำ
ต่อมาดูผลของ γ ต่อ RR เมื่อใช้ α = 0.8 คงที่ ผลที่ได้แสดงดังตาราง (ค่า BRR, CRR คำนวณโดยใช้ค่าเฉลี่ยเลขคณิตของทุกเพลง)
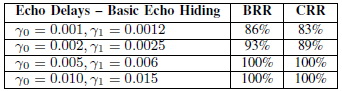
เห็นว่าการใช้ γ ที่มีค่ามาก ทำให้ RR สูง แต่กระนั้น ก็ทำให้ผู้ฟังสามารถได้ยินเสียง echo
ต่อมา ดูผลของ α ต่อ RR เมื่อใช้ γ0 = 0.001 และ γ1 = 0.0012 คงที่ ผลที่ได้แสดงดังตาราง
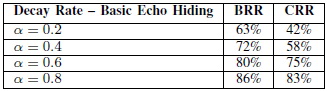
เป็นไปตามคาด คือ ยิ่ง α มีค่าสูง, RR ก็สูงตาม เพราะที่ α ต่ำ เราจะแยกระหว่าง echo กับ noise ไม่ค่อยออก
ต่อมา ผู้เขียนลองเปลี่ยนไปใช้เทคนิค echo hiding แบบต่าง ๆ ดูว่าแต่ละแบบให้ RR เป็นอย่างไรบ้าง เมื่อ α = 0.8, γ0 = 0.001 และ γ1 = 0.0012 คงที่ ผลลัพธ์ที่ได้แสดงดังตาราง

ต่อมา เป็นการทดสอบ robustness โดยมีการโจมตี 3 แบบ คือ (1) เพิ่ม Gaussian white noise ทำให้ SNR = 30 dB, (2) เปลี่ยน sampling rate จากเดิม 44.1 k เป็น 22.05 k แล้วอั๊พกลับเป็น 44.1 k แซมเปิ้ลต่อวินาที, (3) แปลง WAV เป็น 128 kbps MP3 แล้วแปลงกลับเป็น WAV
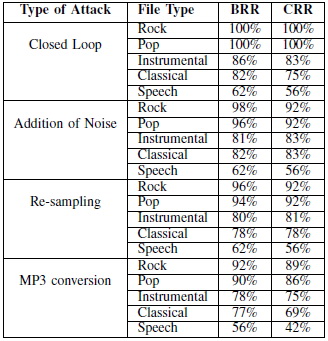
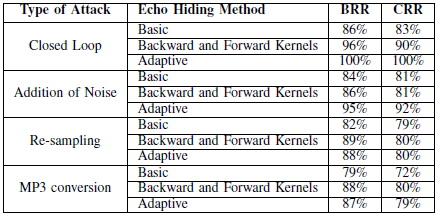
ผลจากตารางต่อไปนี้แสดงให้เห็นว่าชนิดของเพลง กับ RR เมื่อผ่านการโจมตีแบบต่าง ๆ แล้ว มีความสัมพันธ์กันอย่างไร ส่วนตารางถัดไปแสดง RR เมื่อใช้เทคนิคแบบต่าง ๆ การทดลองทั้งหมดทำที่ α = 0.8, γ0 = 0.001 และ γ1 = 0.0012
ต่อมา ผู้เขียนจะลองพัฒนาเทคนิค echo hiding โดยเข้ารหัส T-code ก่อนเอาไปฝังในเพลง ได้ผลลัพธ์ดังตาราง
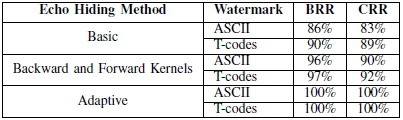
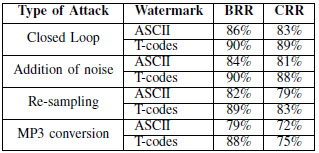
เห็นว่า RR เพิ่มขึ้นนะครับ แต่ก็ไม่ค่อยมากเท่าไร นอกจากนี้ ในตอนท้ายผู้เขียนยังกล่าวถึงข้อดีของการใช้ T-code อีก 2 อย่างคือ ใช้จำนวนบิตน้อยกว่า ASCII เท่ากับเพิ่ม capacity กับ อาจเป็นการเพิ่ม security ไปในตัว เพราะผู้อื่นไม่รู้ว่ากำลังใช้ T-code
| Create Date : 15 มิถุนายน 2556 |
| Last Update : 16 มิถุนายน 2556 17:30:33 น. |
|
0 comments
|
| Counter : 1822 Pageviews. |
 |
|
|
|
|

