|
|
A New Audio Watermarking Scheme Based on Singular Value Decomposition and Quantization
เนื้อหาตอนนี้สรุปจากบทความในชื่อเดียวกันของ Vivekananda Bhat K กับ Indranil Sengupta ตีพิมพ์ใน Circuits Systems and Signal Processing Vol 30 Issue 5 หน้า 915-927 ปี 2011 ผู้เขียนเสนออัลกอริทึมสำหรับ audio watermarking ที่ robust (หมายถึง ลายน้ำยังคงอยู่แม้สัญญาณเสียงจะถูกโจมตี ไม่ว่าโดยเจตนาหรือไม่เจตนา) และ blind (หมายถึง การดึงข้อมูล watermark ออกมาจากสัญญาณเสียงนั้น สามารถกระทำได้โดยไม่ต้องอาศัยสัญญาณเสียงต้นฉบับ) โดยใช้เทคนิค Singular Value Decomposition (SVD) กับ Quantization Index Modulation (QIM)
SVD เป็นการแยกตัวประกอบ (decomposition) ของเมตริกซ์ Hpxp ใด ๆ ให้อยู่ในรูปของผลคูณของเมตริกซ์ 3 ตัว Hpxp = UDVT ในบทความนี้ ผู้เขียนสร้างให้ H เป็นเมตริกซ์จัตุรัสขนาด pxp (แต่ตามทฤษฎีบทนั้น เมตริกซ์ที่เราจะนำมาแยกตัวประกอบไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัส) U กับ V เป็น orthogonal matrix (หมายความว่า UUT = UTU = I และ VVT = VTV = I หรือพูดอีกอย่างหนึ่งว่า UT = U-1 และ VT = V-1) โดยแต่ละคอลัมน์ของ U กับ V คือ eigenvector ของ HHT กับ HTH ตามลำดับ (หายังไง? ตัวอย่างขั้นตอนการหา 1. คำนวณ HHT 2. หา eigenvalue (λi) พร้อม eigenvector (U'i) ที่สัมพันธ์กับ eigenvalue นั้น กล่าวคือ เราหาค่า λi และ U'i ที่สอดคล้องกับสมการ (HHT)U'i = λiU'i 3. สร้างเมตริกซ์ U' จาก eigenvector U'i โดยเรียงลำดับเวกเตอร์ตามลำดับค่า λi จากมากไปน้อย (นั่นคือ เวกเตอร์สำหรับค่า λ มากที่สุดอยู่คอลัมน์แรก) 4. ดำเนินการตามขั้นตอน Gram-Schmidt orthonormalization กับแต่ละคอลัมน์ของ U' เพื่อเปลี่ยนเวกเตอร์แต่ละตัวให้เป็น orthonormal vector (ทุกเวกเตอร์มีขนาดเท่ากับ 1 และ orthogonal ซึ่งกันและกัน) ผลลัพธ์ที่ได้นี่แหละครับคือ U) สำหรับ D คือ diagonal matrix ที่ค่าตามแนวทแยงมุมหลักเท่ากับรากที่สองของ λi เรียงจากมากไปน้อย และไม่เท่ากับศูนย์ (D11 = λ ที่มีค่ามากที่สุด) ค่ารากที่สองของ eigenvalue ซึ่งเป็น element ของ D นี่แหละครับที่เราเรียกว่า Singular Value (SV)
ผู้เขียนบอกว่า SVD-based watermarking scheme ส่วนใหญ่นั้น ฝัง watermark bits ด้วยวิธีการดัดแปลงค่า SV, คำถาม ทำไมเลือกเปลี่ยนค่า SV? มันมีประโยชน์หรือข้อดีอย่างไร?
ผู้เขียนอ้างข้อดีของการจัดการกับค่า SV ไว้ดังนี้ (1) การเปลี่ยนค่า SV ไม่กระทบต่อคุณภาพของสัญญาณอย่างมีนัยสำคัญ (2) SV เป็นปริมาณที่ไม่ผันแปร (invariant) ภายใต้การดำเนินการประมวลผลสัญญาณทั่ว ๆ ไป ข้อนี้หมายความว่า หลังจากที่สัญญาณถูกดำเนินการบางอย่างแล้วนั้น ค่า SV จะยังคงเดิม (3) ขนาดของเมตริกซ์จากการแปลง SVD ไม่ตายตัว และเมตริกซ์ไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัส (4) สมบัติทางพีชคณิตของ SV และ (5) วิธีการนี้ง่าย ไม่ซับซ้อน และให้ผลลัพธ์ที่ดี
ลองมาดูขั้นตอนการฝังข้อมูลกัน จากรูปด้านล่าง เราจะฝัง watermark image (W) ขนาด M x M บิต W = {w(i,j), 1 ≤ i ≤ M, 1 ≤ j ≤ M} ซึ่งเป็น binary image หรือ w(i,j) ∈ {0,1} คือ pixel value ที่ตำแหน่ง (i,j)
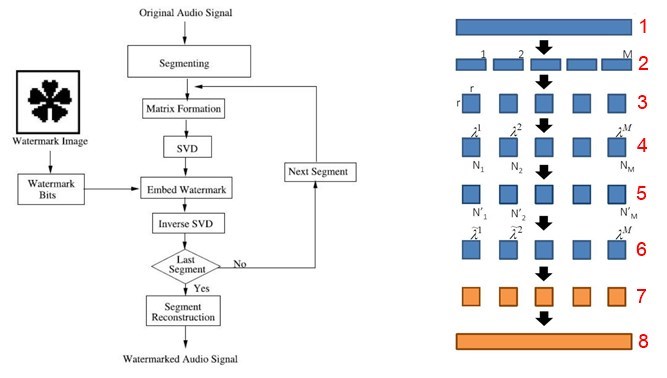
เริ่มต้นจาก ตัดสัญญาณเสียง A (เลข 1 สีแดง) ออกเป็นท่อน ๆ ท่อนละ r x r บิต (r เป็นพารามิเตอร์ตัวหนึ่งที่จะถูกปรับแต่งในการทดลองเพื่อ trade-off ระหว่าง imperceptibility, robustness กับ data payload) จำนวน M x M ท่อน (เลข 2 สีแดง, ตรงนี้ผมสร้างรูปผิดนิดหน่อยนะครับ ตัวอักษร M บนแท่งสีฟ้าขวามือสุด ที่ถูกจะต้องเป็น M x M แต่ขี้เกียจสร้างรูปใหม่ล่ะ เหตุผลที่ผู้เขียนแบ่ง A ออกเป็น M x M ท่อน ก็เพื่อจะฝังแต่ละท่อนด้วย watermark bit แต่ละบิตของ watermark image) จากนั้น นำแต่ละท่อนมีสร้างเป็นเมตริกซ์ (บล็อก 2-D) Bj (แสดงด้วยเลข 3 สีแดง) แล้วทำ SVD กับแต่ละ B เราก็จะได้ค่า SV ถ้ากำหนดให้ λj = (λj1, λj2, ..., λjr) เป็นเวกเตอร์ของ SV ของบล็อก Bj (สัญลักษณ์ λ ตั้งแต่ย่อหน้านี้เป็นต้นไป ไม่ใช่ตัวเดียวกับ λ ในย่อหน้าที่ 2 นะ ผมใช้ λ ในย่อหน้าที่ 2 แทน eigenvalue เพราะเป็นสัญลักษณ์สากลที่ใช้กันในทางคณิตศาสตร์ และใช้ λ แทน SV ในย่อหน้านี้เพราะผู้เขียนบทความใช้ λ = SV อย่าลืมว่า SV เป็นค่ารากที่สองของ eigenvalue นะครับ) เราใช้ λj ในการหา Euclidean norm ด้วยสมการ Nj = |λj| = √(∑(λji)2) เมื่อ i มีค่าตั้งแต่ 1 ถึง r
เราคำนวณ norm ของแต่ละบล็อก เพราะจะดัดแปลงค่าของมัน (ขั้นตอนการดัดแปลงค่านี้แหละครับคือ quantizing หรือพูดอย่างเจาะจง เทคนิคที่ใช้คือ QIM) โดยกำหนด Yj = Nj mod Δ เมื่อ Δ เป็นพารามิเตอร์อีกตัวที่จะถูกปรับแต่งในการทดลอง ชื่อเรียกของ Δ คือ quantization coefficient ทีนี้ค่าของ norm ดัดแปลง หรือ N'j นั้นจะขึ้นอยู่กับ watermark bit ถ้า watermark bit ที่เราจะฝังลงในบล็อกดังกล่าวคือ 1 และถ้า Yj < Δ/4 ค่า N'j = Nj - Δ/4 - Yj แต่ถ้า Yj ≥ Δ/4 ค่า N'j = Nj + 3Δ/4 - Yj กรณีที่ watermark bit คือ 0 และ Yj < 3Δ/4 ค่า N'j = Nj + Δ/4 - Yj แต่ถ้า Yj ≥ 3Δ/4 ค่า N'j = Nj + 5Δ/4 - Yj หลังจากผ่านขั้นตอนนี้ เราจะได้ norm ใหม่ของแต่ละบล็อก (เลข 5 สีแดง) ใช้ norm ใหม่, norm เก่า และเวกเตอร์ของ SV (λj) ของแต่ละบล็อก Bj ในการคำนวณเวกเตอร์ดัดแปลง (เขียนแทนด้วย λ*j) ของ SV ด้วยสมการ λ*j = λjN'j/Nj ขั้นตอนต่อมาใช้ λ*j คำนวณเมตริกซ์ดัดแปลง B*j โดยใช้ inverse SVD หรือ B*j = ∑λ*jiUi(j)VTi(j) เมื่อ i มีค่าตั้งแต่ 1 ถึง r ซึ่ง B*j ก็คือบล็อกข้อมูลเสียง (สีส้ม) ที่เราฝัง watermark bit ไปแล้วนั่นเอง
ขั้นตอนการดึง watermark image ออกมาจาก watermarked audio signal แสดงดังรูป
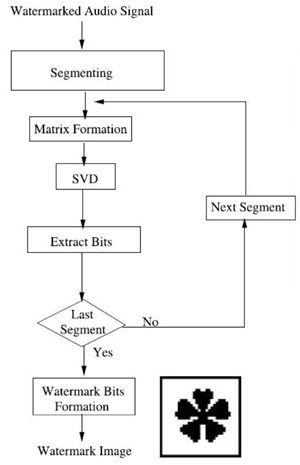
เริ่มต้นด้วยการนำ watermarked audio signal มาทำเป็นบล็อกขนาด r x r จำนวน M x M บล็อกเหมือนเดิม และแต่ละบล็อกก็ทำ SVD ทำนองเดียวกับขั้นตอนการฝัง คำนวณค่า norm ของแต่ละบล็อกออกมา จากนั้นเราสามารถบอกได้ว่า watermark bit ที่ฝังลงในบล็อกนั้นคืออะไรจากการดูว่า Yj < Δ/2 หรือไม่ เมื่อ Yj = Nj mod Δ ถ้า Yj < Δ/2 หมายความว่า watermark bit = 0 แต่ถ้า Yj ≥ Δ/2 เราก็จะรู้ว่า watermark bit = 1
บทความนี้ประเมินความสามารถของอัลกอริทึม 2 ด้าน คือ ด้านคุณภาพเสียง (imperceptibility) และด้านความทนทานต่อการถูกโจมตี (robustness) สำหรับ imperceptibility test นั้น ผู้เขียนได้ทดสอบทั้ง subjective และ objective test โดยใช้ subjective difference grade (SDG) กับ objective difference grade (ODG) เป็นตัวชี้วัดตามลำดับ ใน subjective test ผู้เข้าร่วมทดสอบจะได้ฟังไฟล์เพลง 8 เพลง (4 ประเภทเพลง ประเภทละ 2 เพลง) แต่ละเพลงจะได้ยิน 2 ครั้ง ครั้งหนึ่งเป็นไฟล์เสียงต้นฉบับ ส่วนอีกครั้งจะเป็นไฟล์เสียงหลังจากฝังข้อมูลลงไปแล้ว เขาจะต้องให้เกรด (SDG) 0 ถึง -4 เพื่อบอกว่าเขาสามารถรับรู้ถึงความแตกต่างระหว่างคุณภาพเสียงของไฟล์ทั้งสองของเพลงเดียวกันนั้นแค่ไหน โดยเกรด 0 คือ ไม่รู้สึกถึงความแตกต่างเลย (หมายความว่า คุณภาพเสียงหลังจากฝังลายน้ำดีมาก) และ -4 คือ แตกต่างกันจนถึงขั้นรับไม่ได้อย่างแรง (คุณภาพเสียงหลังจากฝังลายน้ำแล้วห่วยมาก) กรณี objective test ก็มีการให้เกรดเหมือนกับคนล่ะครับ เพียงเปลี่ยนจากคนตัดสินเป็นเครื่องจักรตัดสิน เครื่องจักรตัดสินตามมาตรฐาน PEAQ (perceptual evaluation of audio quality) ตามที่กำหนดไว้ใน ITU-R BS.1387

robustness test ใช้การคำนวณ NC (normalized correlation) กับ BER (bit error rate) เป็นตัวชี้วัด NC จะบอกว่า watermark image W กับ extracted watermark image W* เหมือนกันแค่ไหน ดูจากสมการข้างบน คงเห็นได้ไม่ยากว่าถ้า W* = W จะทำให้ NC = 1 นี่คือค่าที่เราต้องการ ส่วน BER บอกว่า W* กับ W มีจำนวนบิตที่แตกต่างกันกี่บิตเมื่อเทียบกับจำนวนบิตทั้งหมด ซึ่งก็คือ M x M วิธีเปรียบเทียบก็ทำตรงไปตรงมาด้วยการนับผลรวมของ w(i,j) xor w*(i,j) ถ้า W* = W ค่า BER = 0
สำหรับการทดลองในบทความนี้ ผู้เขียนเลือกใช้ r = 15 และ Δ = 0.59 พารามิเตอร์สองตัวนี้ถูกเลือกขึ้นมาเพื่อ trade-off ระหว่าง requirement ต่าง ๆ ของ watermarking ที่ขัดแย้งกันเอง พูดได้ว่า ค่า r กับ Δ ที่ผู้เขียนเลือกมานี้เป็นค่าที่ทำให้ SDG, ODG, NC สูงสุด ขณะที่ BER ต่ำสุด ผลลัพธ์ SDG กับ ODG แสดงดังตาราง
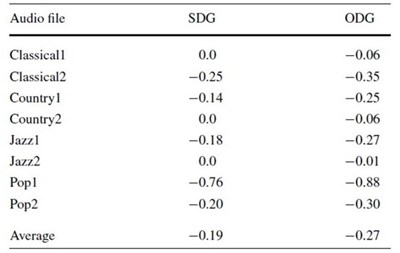
เห็นว่าเกรดใกล้เคียง 0 มาก แปลว่า คนและเครื่องจักรแยกความแตกต่างระหว่างคุณภาพของเสียงต้นฉบับกับเสียงที่ฝังข้อมูลลงไปแล้วแทบไม่ออก ตารางต่อมาแสดงผลลัพธ์เปรียบเทียบ watermark image ต้นฉบับกับ extracted watermark image ที่ดึงจาก watermarked audio signal หลังผ่านการโจมตีแบบต่าง ๆ ตัวเลขใต้ภาพแสดงค่า NC ซึ่งส่วนใหญ่ใกล้เคียงหนึ่ง นั่นหมายถึง robustness ของอัลกอริทึมที่ผู้เขียนเสนอ

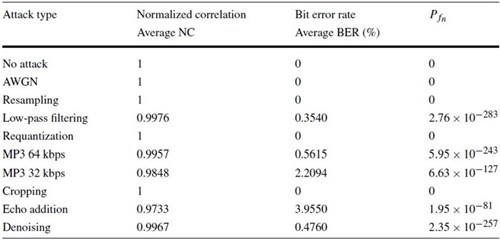
ตารางสุดท้าย แสดงค่า NC และ BER เมื่อถูกโจมตีด้วยการประมวลผลสัญญาณดิจิทัลแบบต่าง ๆ ในคอลัมน์สุดท้ายคือ Pfn หมายถึง โอกาสเกิด false negative error หรือ error ที่เกิดจากตัวถอดรหัสบอกว่า watermarked signal ไม่เป็น watermarked signal (นอกจาก false negative error ยังมี false positive error ที่ตัวถอดรหัสบอกว่า unwatermarked signal เป็น watermarked signal แต่เนื่องจาก Ppn ไม่เกี่ยวข้องกับโอกาสเกิด BER ผู้เขียนจึงไม่ให้ความสนใจ) ข้อมูลในตารางนี้แสดงให้เห็น robustness ได้เป็นอย่างดี
| Create Date : 14 เมษายน 2556 |
| Last Update : 14 เมษายน 2556 14:15:00 น. |
|
0 comments
|
| Counter : 5487 Pageviews. |
 |
|
|
|
|
|

