Research of Improved Echo Data Hiding: Audio Watermarking based on Reverberation
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ G. Nain, S. Wang กับ Y. Ge ใน Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 117-180 ปี 2007 ที่ Honolulu
เทคนิค echo-hiding ที่ผมได้เล่ามาหลายตอนก่อนหน้านี้ อย่างมากเราเพิ่ม echo เข้าไปไม่เกิน 4 ลูกใช่มั้ยครับ แต่สำหรับเทคนิคที่ผ้เขียนเสนอในบทความนี้ คีย์เวิร์ดของมันคือ reverberation ซึ่งก็ไม่ใช่อะไรหรอก นอกจาก echo จำนวนมากที่ผสมปนเปกันแบบซับซ้อน เรายังคงใช้ kernel 2 ตัวในการฝัง "0" กับ "1" แต่คำถามอยู่ที่ เราจะหา kernel ยังไง นี่แหละครับประเด็น และคำตอบของผู้เขียนคือ หาจาก reverberation (หรือพูดให้เจาะจง room impulse response) ที่จุด 2 จุดในห้อง ใช้จุดหนึ่งแทนการฝัง "0" และอีกจุดสำหรับฝัง "1" โดยวิธีการหา room ir ของผู้เขียนคือ image method และพารามิเตอร์ที่ใช้หา room ir ยังทำหน้าที่เป็น secret key ที่จำเป็นต้องใช้ในการดึงลายน้ำออกมา นั่นเท่ากับเป็นการเพิ่ม security อีกทอดหนึ่ง

สมมติว่าแหล่งกำเนิดเสียงอยู่ที่ (sx, sy, sz) และเลือกผู้ฟัง 2 จุด พิกัด (lx1, ly1, lz1) กับ (lx2, ly2, lz2) คำนวณ room ir h1(n) กับ h2(n) จากนั้นใช้มันสร้าง kernel function f1(n) = δ(n) + h1(n) กับ f2(n) = δ(n) + h2(n) ซึ่ง room ir จะอยู่ในรูป h(n) = α1δ(n-n1) + α2δ(n-n2) + ... + αLδ(n-nL) เมื่อ L คือ ความยาวของ room ir (หรือจำนวน echo นั่นแหละครับ) ถ้า xi(n) คือ สัญญาณต้นฉบับ เราจะได้สัญญาณที่ฝังลายน้ำ xwi(n) = xi(n)*f(n) เมื่อสัญลักษณ์ * แทน linear convolution ตรงนี้เห็นว่า ขั้นตอนต่าง ๆ เหมือนเทคนิคในตระกูล echo-hiding ทั่ว ๆ ไป ต่างกันแค่วิธีการหา kernel function เท่านั้นเอง
block diagram ขั้นตอนการดึงลายน้ำออกมาแสดงดังรูป

จากรูป หลังหา cepstrum ของ xwi(n) แล้ว ก็เอา cepstrum นั่นมาหา cross-correlation กับ h1(n - n11 กับ h2(n - n21 ถ้าหากบิตที่ฝังอยู่คือ "1" เราจะเห็น peak ที่ n1 ของ d1(n) แต่ไม่เห็นของ d2(n) ดังรูป

ถ้า σwn1 เป็น ส่วนเบี่ยงเบนมาตรฐานของ d1(n) ยกเว้นค่าที่ n1(n) เนื่องจากที่ตำแหน่งดังกล่าวเป็นค่า peak และ σwn2 เป็น s.d. ของ d2(n) ยกเว้นที่ค่าสูงสุดเช่นกัน เราจะใช้ค่า r(i) = [d1(max)/σwn1]/[d2(max)/σwn2] เป็นตัวตัดสินใจว่าบิตที่ฝังคือ "0" หรือ "1" ถ้า r(i) > T (เป็น threshold ค่าหนึ่ง) เราจะบอกว่าบิตที่ฝังอยู่คือ "1" แต่ถ้า r(i) < T บิตที่ฝังคือ "0"
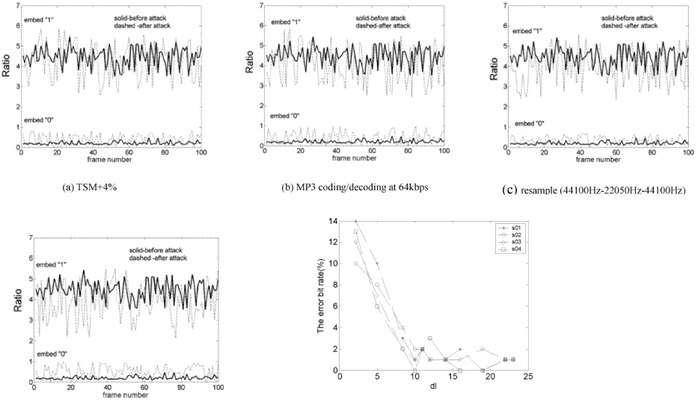
ผลการทดลอง: รูปด้านล่างแสดงความสัมพันธ์ระหว่าง dl = sqrt[(lx1-lx2)2 + (ly1-ly2)2 + (lz1-lz2)2] กับ correct response ของเพลง S01 - S04 เห็นว่า ยิ่ง dl น้อย correct response จะยิ่งดี และสมบัติ imperceptibility จะดีมากถ้า dl < 15

การทดลองที่เลือกใช้ dl = 8.378 เมื่อผ่านการโจมตีแบบต่าง ๆ แล้วพบว่า error bit rate < 4% กราฟด้านล่างแสดง ratio curve ก่อนและหลังการโจมตี
| Create Date : 16 กรกฎาคม 2556 |
| Last Update : 16 กรกฎาคม 2556 9:29:39 น. |
|
0 comments
|
| Counter : 1140 Pageviews. |
 |
|
|
|
|

