|
Flaw in SVD-based Watermarking
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้ผมสรุปจากบทความในชื่อเดียวกันของ L. Lamarche, Y. Liu กับ J. Zhao จาก Canadian Conference on Electrical and Computer Engineering ที่ออตตาว่าปี 2006 ในบทคัดย่อของบทความ Lamarche อ้างถึง Zhang กับ Li (2005) ที่ได้วิจารณ์ image watermarking ของ Liu กับ Tan ซึ่งใช้เทคนิค SVD ที่ได้เสนอไปเมื่อปี 2002 ว่ามีจุดบกพร่อง และเนื่องจาก Ozer ได้นำเทคนิคดังกล่าวมาประยุกต์ใช้กับ audio (ไอเดียของ Ozer ดูได้จาก An SVD-Based Audio Watermarking Technique) Lamarche และคณะจึงจะสำรวจและทดสอบว่า วิธีการของ Ozer จะมีจุดบกพร่องแบบเดียวกันหรือไม่ อันนี้คือแก่นของบทความ ในการชี้จุดผิดของการทำลายน้ำภาพนั้น Zhang ให้เหตุผลว่า ในส่วนตรวจจับลายน้ำต้องอาศัยเมตริกซ์ 2 ตัวซึ่งเราถือว่ารู้ก่อนล่วงหน้า เจ้าเมตริกซ์สองตัวนี้ถูกสร้างขึ้นระหว่างขั้นตอนฝังลายน้ำนะครับ (ถ้าคุณอ่านตอนที่แล้วคงจำได้, ถ้าจำไม่ได้ เดี๋ยวผมจะพูดถึงซ้ำอีกทีในเนื้อหาตอนนี้ ช่วงต่อไป) และการตรวจจับดังกล่าว ขึ้นอยู่กับเมตริกซ์ 2 ตัวนี้มากเกินไป ทำให้อัตราการตรวจจับที่เป็น false positive มีค่าสูง สำหรับ Lamarche เมื่อได้ทดลองแล้วก็พบอย่างเดียวกัน
ทบทวนเทคนิคของ Ozer รูปด้านล่างแสดงการฝัง
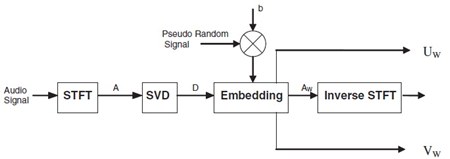
นำสัญญาณเสียงมาแปลง STFT แล้วสร้างเมตริกซ์ A ขนาด FxM (ถ้าอ่านเปเปอร์ต้นฉบับ ผู้เขียนจะเขียน M by F matrix ซึ่งน่าจะพิมพ์ผิดนะ เพราะในส่วนถัดมา เราจะเห็นค่า i รันจาก 1 ถึง F และ j รันจาก 1 ถึง M) ต่อมา แยกเมตริกซ์ดังกล่าวด้วย SVD ได้ A = UDVT เมื่อ D เป็นเมตริกซ์ singular value, D = diag(δ1, δ2, ..., δr) เมื่อ δi คือ sv
วิธีการฝังของ Ozer คือการเปลี่ยนเมตริกซ์ D ด้วย DW พูดอีกอย่างว่า ผลคูณของ UDWVT ได้ AW หรือเมตริกซ์ที่เมื่อแปลง STFT ผกผันแล้วจะได้สัญญาณเสียงที่ฝังลายน้ำลงไปเรียบร้อยแล้ว ทีนี้ ในการสร้าง DW เขาจะสร้าง WD ขึ้นมาก่อน โดยเมื่อเอา WD มาแยกด้วย SVD เราจะได้ WD = UWDWVWT
WD สร้างจากการดัดแปลงเมตริกซ์ WFxM หรือ watermark carrier ซึ่งแต่ละ element เป็นเสมือน noise ด้วยค่า δi, a = embedding strength กับ b = polarity {-1, 1} ของ watermark ดังสมการ
WD(i,j) = δi + abδiw(i,j)
โอเคนะครับ หลังจากได้ WD เอามันมาแยก SVD เพื่อให้ได้ DW แล้วเอา DW ไปแทนที่ D ใน UDVT เราก็จะได้ AW เอาไปแปลง inverse STFT ก็จบ ทั้งนี้ทั้งนั้น ในการตรวจจับลายน้ำ ทางฝั่งตรวจจับจะต้องใช้เมตริกซ์ 2 ตัวคือ UW กับ VW ตรงนี้แหละครับที่เปเปอร์นี้อ้างว่าเป็นตัวปัญหา (จะจริงเท็จแค่ไหน เท่าที่รู้ตอนนี้ ผมยังไม่เห็นมีใครยืนยันซ้ำนะ)
ภาคตรวจจับลายน้ำมี diagram ดังรูป
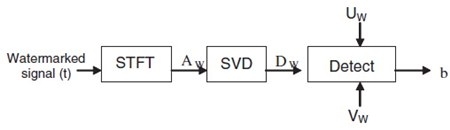
เอา watermarked signal มาแปลง STFT เพื่อสร้างเมตริกซ์ AW จากนั้นใช้ SVD แยก AW เพื่อให้ได้ D'W ใช้ D'W ร่วมกับ UW และ VW ที่รู้ก่อนล่วงหน้าจากขั้นตอนการฝัง เพื่อสร้าง W'D = UWD'WVWT หลังจากนั้นใช้ W'D หา W' จาก W' = D-1(W'D - D)/a สุดท้ายในการตัดสินว่าบิตที่ฝังคืออะไร เราหา correlation ระหว่าง W' กับ W (original watermark) โดยถ้า ∑wijw'ij สำหรับทุกค่า i, j เป็นบวก เราจะตีความว่า b = 1 (bit 1) นอกนั้น b = -1 (bit 0)
ในส่วนการทดลอง ผู้เขียนบอกว่าไม่สามารถทำตามขั้นตอนที่ Ozer เสนอได้ เพราะหลังจากทำตามเปเปอร์ของ Ozer สร้าง WD ขึ้นมาแล้ว watermarked signal นั้นมี noise เยอะมาก! จึงดัดแปลงสมการตอนฝังข้อมูลเป็น WD(i,j) = D(i,j) + abD(i,j)w(i,j) แต่พอดัดแปลงอย่างนี้แล้ว มีปัญหาตอน detect อีก จึงดัดแปลงอีกครั้ง เป็น WD(i,j) = D(i,j) + abw(i,j) ฉะนั้นสมการตอนตรวจจับจึงต้องเปลี่ยนตาม เป็น W' = (W'D - D)/a
การทดสอบที่ 1 ลายน้ำ Wr สำหรับ bit = 1 ถูกฝังลงในสัญญาณเสียงพูด X0 ได้สัญญาณ XW พร้อมเมตริกซ์ UW กับ VW ทีนี้ แทนที่จะใช้ XW เป็น input สำหรับ detection stage ก็ใช้สัญญาณ Y ซึ่งเป็นเสียงพูดอีกอันหนึ่งแทน สัญญาณ Y นี้ไม่มีลายน้ำนะครับ และเป็นคนละอันกับ X0 ปรากฏว่า ใช้ Y ร่วมกับ UW และ VW เขาก็สามารถตรวจจับลายน้ำได้ รูปด้านล่าง เอาลายน้ำที่ดึงมาจาก Y หาความคล้ายกับลายน้ำที่สร้างอย่างสุ่ม 200 ตัว โดยตัวที่ 100 เป็นลายน้ำของจริง แต่ในความเป็นจริง Y ไม่มีลายน้ำ!
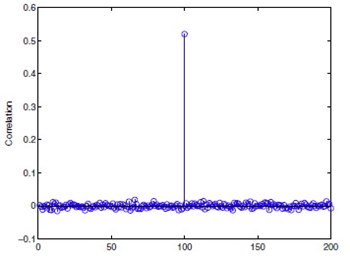
การทดสอบที่ 2 โจมตี UW กับ VW โดยการเติม noise เล็ก ๆ U'W = UW + cUNoise และ V'W = VW + cVNoise เมื่อ UNoise กับ VNoise เป็น random noise matrices ที่มีการแจกแจงแบบปกติ และ c คือ noise variance กรณีที่ c = 10 เมื่อดึงลายน้ำจาก XW โดยใช้ U'W กับ V'W และหาความเหมือนกับลายน้ำที่สุ่ม 200 ตัวโดยตัวที่ 100 เป็นลายน้ำจริงจะได้ผลลัพธ์ดังรูป เห็นว่ากรณีนี้ correlation กับลายน้ำสุ่มไม่ได้ใกล้ 0 หมายความว่า false positive rate สูง

และเมื่อคำนวณ BER เมื่อทดสอบ 1000 ครั้งที่ค่า c = 1, 10 และ 100 ตามลำดับพบว่าเกิด error 47 ครั้งสำหรับทั้ง 3 กรณี นั่นคือ BER = 4.7% สำหรับการใส่ noise ลงในเมตริกซ์ ผู้เขียนสรุปว่า ภาคตรวจจับของ Ozer ขึ้นอยู่กับเมตริกซ์ที่สร้างตอนฝังและส่งผ่านมาใช้ตอนตรวจจับมากเกินไป และไม่ขึ้นอยู่กับ watermarked signal ที่ใช้ในการทดสอบ
ถ้าผลจากเปเปอร์นี้จริง วิธีของ Ozer น่าจะเจอปัญหาซีเรียส และเป็นไปได้ว่า กลุ่มของเทคนิคที่ส่งผ่าน UW กับ VW น่าจะเจออะไรที่คล้าย ๆ กัน, เท่าที่ได้ review มาถึงขณะนี้ ผมยังไม่เจอใครทดสอบการขึ้นอยู่กับเมตริกซ์สองตัวนี้ในกลุ่มเทคนิคที่คล้ายคลึงกับงานของ Ozer นะ
| Create Date : 27 สิงหาคม 2556 | | |
| Last Update : 27 สิงหาคม 2556 20:59:32 น. |
| Counter : 1282 Pageviews. |
| |
|
 |
|
|
|
An SVD-Based Audio Watermarking Technique
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้ผมสรุปจากบทความในชื่อเดียวกันของ H. Ozer, B. Sankur กับ N. Memon จาก Workshop on Multimedia and Security ครั้งที่ 7 ปี 2005 ที่ New York ไอเดียของบทความถูกนำไปอ้างถึงและต่อยอดในอีกหลายบทความนะครับ ซึ่งเป็น SVD-based ที่แตกต่างจากเทคนิคที่ผมเคยเล่าไปก่อนหน้า (ดู A New Audio Watermarking Scheme Based on Singular Value Decomposition and Quantization) และผลลัพธ์ที่ได้จากเทคนิคนี้ robustness สูงมาก กระนั้น ในปี 2006 มีบทความของ L. Lamarche และคณะจาก Canadian Conference on Electrical and Computer Engineering ที่ออตตาว่า ออกมาแย้งถึงการตีความ robustness สูงเกินไปเนื่องจาก BER ที่ต่ำนั้นเป็นผลสืบเนื่องของ false positive detection rate ที่สูง รายละเอียดบทความของ Lamarche (2006) ผมจะเอามาเล่าบล็อกตอนต่อไป สำหรับตอนนี้เราจะศึกษาไอเดียของ Ozer และคณะกันก่อน
ขั้นตอนการซ่อนลายน้ำ เริ่มจาก เอาสัญญาณเสียงมาแปลง STFT สมการ analysis และ reconstruction ของ STFT คือ
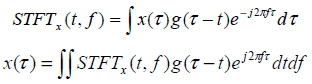
เมื่อ g(t) เป็น window function ที่เลื่อนไปคูณกับสัญญาณเสียง x(t) ตลอดย่านที่มีสัญญาณ x(t) ก่อนเอาผลลัพธ์จากการคูณนั้นมาแปลงฟูริเยร์ หลังจากแปลง เราจะได้ฟังก์ชั่นในโดเมนความถี่และเวลา ซึ่งเอามาสร้างเป็นเมตริกซ์สองมิติขนาด FxM เมื่อ F คือ จำนวนเฟรม (ขึ้นอยู่กับความยาวของ x(t)) และ M คือ ขนาดของเฟรม
ต่อมา เอาเมตริกซ์ดังกล่าวมาแยกด้วย SVD: AFxM = UDVT เมื่อ D เป็น diagonal matrix ขนาด FxM ที่มี elements บนเส้นทแยงมุม หรือที่เรียกว่า singular value (sv) จำนวน min(F,M) ตัว ส่วน U กับ V เป็น orthogonal matrix ขนาด FxF กับ MxM ตามลำดับ สมบัติที่สำคัญของ SVD คือ sv ไม่เปลี่ยนแปลงภายใต้ orthogonal transformation
หลังจากได้ D แล้ว เราจะฝังลายน้ำลงใน D โดยใช้ watermark (ซึ่งเป็นลำดับของรหัสเลขฐานสอง) ร่วมกับ pseudo-random signal เพื่อกระจายกำลังงานของ watermark bit ซึ่งเจ้าสัญญาณ pseudo-random ตัวนี้ ในเปเปอร์ผู้เขียนเรียกว่า watermark carrier W = {w(i,j)} เป็นเมตริกซ์ขนาด FxM ที่แต่ละ element มีลักษณะคล้าย random noise
วิธีฝัง เริ่มจากสร้าง WD จาก wD = δi + abδiw(i,j) สำหรับ i = 1, 2, ..., F และ j = 1, 2, ..., M เมื่อ δi คือ sv ของ A, a คือ embedding strength หรือ scaling factor และ b ∈ {-1, 1} เป็น polarity ของลายน้ำที่จะฝัง
ต่อมา เอา WD มาแยกด้วย SVD อีกที WD = UWDWVWT สุดท้าย ได้สัญญาณเสียงหลังจากฝังลายน้ำลงไปจากการแปลง inverse STFT ของ AW = UDWVT ขั้นตอนโดยรวมแสดงดังรูป
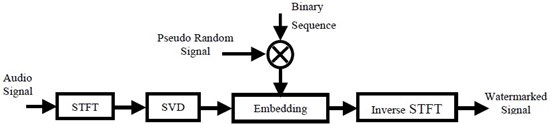
ทางฝั่งตรวจจับลายน้ำ จะถือว่ามีข้อมูลเหล่านี้อยู่ในมือ ได้แก่ UW, VW, D และ key ที่ใช้สร้าง pseudo-random signal ขั้นตอนการตรวจจับลายน้ำก็เสมือนเป็นขั้นตอนย้อนกลับของการฝังลายน้ำ นำสัญญาณเสียงที่ได้รับมาแปลง STFT แล้วสร้างเมตริกซ์ A' จากนั้น กระจาย A' ด้วย SVD
A' = U'D'WV'T
เอา D'W ที่ได้จากขั้นตอนแยก SVD กับ UW และ VW (2 ตัวหลังนี้ ถือว่าทางฝั่งถอดลายน้ำรู้ล่วงหน้าแล้ว) มาหา W'D = UWD'WVWT แล้วใช้ W'D ในการคำนวณ W' จากความสัมพันธ์ aW' = D-1(W'D - D)
เราใช้ key สร้าง W (ซึ่งจะได้เมตริกซ์ของ watermark carrier เหมือนตอนซ่อนข้อมูล) แล้วทำการเปรียบเทียบความเหมือนของ W' กับ W
W'·W = ∑wijw'ij สำหรับทุกค่า i, j
ถ้า W'·W > 0 เราจะบอกว่า b = 1 แต่ถ้า W'·W ≤ 0 เราจะบอกว่า b = -1
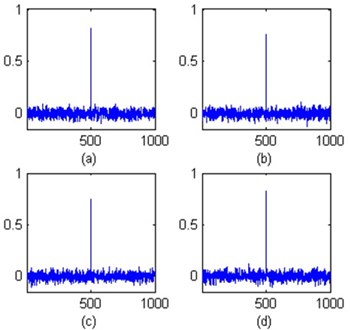
รูปด้านล่างแสดงตัวอย่างการตอบสนองของ detector ต่อ watermark ที่สร้างอย่างสุ่ม 1000 ตัว แกนนอนคือการตอบสนอง ซึ่งดู correlation หรือ similarity score และตำแหน่งที่ 500 เป็นลายน้ำของจริงหลังจากถูกโจมตี 4 แบบ คือ (a) copysample, (b) fft_HLPass, (c) flipsample, (d) zerocross
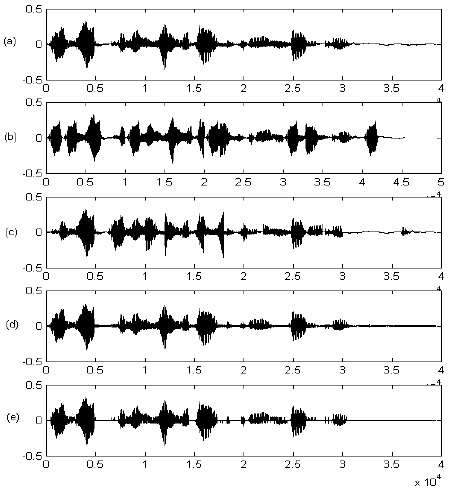
ลักษณะของสัญญาณต้นฉบับและสัญญาณหลังจากถูกโจมตีทั้ง 4 แบบข้างต้นแสดงดังรูป (a) - (e) ตามลำดับ
ผลการทดลอง audibility tests ได้คะแนน PAQM = 0.01 และ MOS = 4.7 ถือว่าดีมากนะครับ ตัวเลขนี้หมายความว่าฟังแยกความแตกต่างระหว่างสัญญาณต้นฉบับกับสัญญาณเสียงที่ใส่ลายน้ำแทบไม่ออก ผลการทดสอบ robustness tests ก็ออกมาดี BER ต่ำมาก ดูตารางที่ 1 และผู้เขียนได้เปรียบเทียบ BER ระหว่าง SVD-based กับ DCT-based แสดงดังตารางที่ 2
| Create Date : 25 สิงหาคม 2556 | | |
| Last Update : 27 สิงหาคม 2556 1:32:24 น. |
| Counter : 1728 Pageviews. |
| |
|
| |
|
|
|
Absolute Thresholds
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
บทนี้พูดถึงความสามารถของ auditory system ในการตรวจจับเสียงเบา ๆ เมื่ออยู่ในสภาพแวดล้อมที่ไม่มีเสียงอื่นอยู่ด้วย
absolute threshold หรือ ขีดเริ่มการได้ยินเสียง คือ ระดับต่ำสุดของเสียงที่หูเราสามารถตรวจจับได้เมื่อไม่มีเสียงอื่น โดยทั่วไป เรามีวิธีวัดระดับต่ำสุดดังกล่าวอยู่ 2 แบบ (1) วัดความดันเสียงที่จุดใดจุดหนึ่งใกล้รูหูหรือในรูหูโดยใช้ไมโครโฟนโพรบอันเล็ก ๆ ยิ่งใกล้ eardrum ยิ่งดี วิธีวัดแบบนี้ต้องระบุตำแหน่งให้ชัดเจนนะครับ เพราะตำแหน่งต่างกันนิดเดียว ให้ผลลัพธ์ที่แตกต่างกันอย่างมากได้สำหรับกรณีความถี่สูง ขีดเริ่ม หรือ threshold ที่วัดด้วยวิธีนี้เรียกว่า minimum audible presure หรือ MAP, (2) วัดระดับเสียงหลังจากเอาผู้ฟังออกจากสนามเสียง (sound field) โดยทำการวัดที่จุดซึ่งเคยเป็นกึ่งกลางศีรษะของผู้ฟัง เรียกค่าขีดเริ่มที่วัดด้วยวิธีนี้ว่า minimum audible field หรือ MAF
เสียงที่เราใช้ป้อนเป็น input ส่วนใหญ่เป็น sinusoidal tone ที่ยาวกว่า 200 ms ทั้งนี้เพราะช่วงความยาวของเสียงมีผลต่อระดับขีดเริ่มการได้ยินเสียง (ถ้าเสียงนานกว่า 500 ms ความยาวของเสียงไม่มีผลต่อ threshold) กราฟขีดเริ่มการได้ยินมักพล็อตในโดเมนความถี่ของ sinusoidal tone ดังรูป
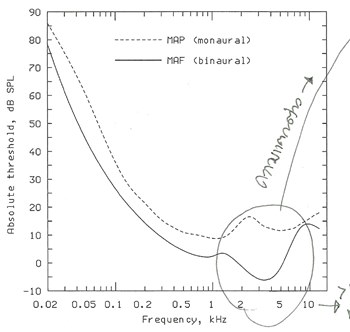
จากรูป เห็นเส้นประ MAP มีวงเล็บ monaural หมายถึง กรณีมีเสียงป้อนเข้ามาที่หูข้างเดียว (ผ่านทางหูฟัง) ส่วน MAF ผู้ฟังตัดสินความดังโดยหูทั้งสองข้าง (binaural) โดยเฉลี่ยนั้น ถ้าใช้สองหู ค่า threshold จะลดลงประมาณ 2 dB SPL เมื่อเทียบกับกรณีหูเดียว เส้นกราฟได้จากข้อมูลเฉลี่ยของผู้ฟังอายุน้อยที่หูปกตินะครับ หมายเหตุ สำหรับผู้ฟังคนใดคนหนึ่งอาจมีค่า threshold สูงหรือต่ำกว่ากราฟนี้ได้ถึง 20 dB SPL ที่บางค่าความถี่ ก็ยังจัดว่าเป็นผู้ฟังที่ปกติอยู่นะ
กราฟ MAP กับ MAF แตกต่างกันชัดเจนในช่วงความถี่ 1.5 - 6 kHz อันนี้เป็นผลจากปากรูหูกับใบหู เพราะการวัดแบบหนึ่งเราต้องยัดโพรบเข้าไปในรูหู ส่วนการวัดอีกแบบ โพรบวางอยู่ในสนามเสียงอิสระไม่ถูกครอบงำด้วยอิทธิพลของปากรูหูกับใบหู ผลต่างของระดับเสียง MAP กับ MAF แสดงดังรูปด้านล่าง
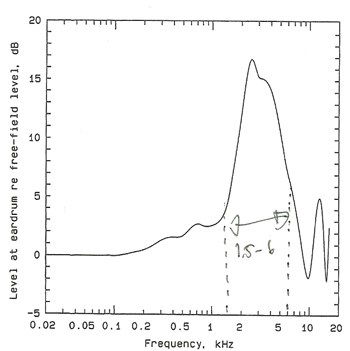
threshold ทั้ง MAP และ MAF จะเพิ่มขึ้นอย่างรวดเร็วที่ความถี่สูงมากและต่ำมาก ส่วนหนึ่งมาจากลักษณะเฉพาะของการส่งผ่านสัญญาณของหูชั้นกลาง ซึ่งส่งผ่านได้ดีในย่านความถี่กลาง ๆ
ความถี่สูงสุดที่สามารถได้ยินได้ขึ้นอยู่กับอายุ ในเด็กนั้นอาจได้ยิน tone ความถี่สูงถึง 20 kHz แต่สำหรับผู้ใหญ่ส่วนใหญ่ ค่า threshold จะเพิ่มขึ้นอย่างรวดเร็วเมื่อความถี่สูงกว่า 15 kHz ส่วนทางฝั่งความถี่ต่ำ ดูเหมือนจะไม่มีขีดจำกัดจำเพาะ Whittle และคณะ (1972) ได้ทดลองวัด threshold สำหรับความถี่จาก 50 Hz ถึง 3.15 Hz พบว่าผลลัพธ์หรือกราฟที่ได้ก็ดูต่อเนื่องกับฝั่งความถี่ที่สูงกว่าดี กระนั้น ที่ 3.15 Hz ขีดเริ่มการได้ยินจะมีค่าอยู่ที่ราว 120 dB SPL
Johnson กับ Gierke (1974) บอกว่า ในความหมายทั่ว ๆ ไปนะ เราไม่ควรพูดว่าได้ยินเสียงที่ความถี่ต่ำกว่า 16 Hz แต่เราตรวจจับมันได้จาก distortion products (ฮาร์มอนิกส์) ที่พวกมันสร้างขึ้นหลังจากผ่านเข้าไปในหูชั้นกลาง หรือจากการสั่นของร่างกาย อย่างไรก็ตาม แนวคิดของ Johnson กับ Gierke ก็ไม่ค่อยเป็นที่ยอมรับเท่าไรนัก
Moller กับ Pederson (2004) บอกว่า สัญญาณ sinusoidal ที่ความถี่ต่ำกว่า 20 Hz นั้นถูกตรวจจับด้วยหูมากกว่าการสั่นของร่างกาย แต่ที่ความถี่ดังกล่าว เราจะไม่ได้ยินเสียงเป็นโทนอลหรือเสียงแบบที่เอามาทำเป็นทำนองเพลง การได้ยินเสียงที่ความถี่ต่ำกว่า 20 kHz มีลักษณะไม่ต่อเนื่อง และมันอาจถูกรับรู้แบบเรารู้สึกถึงความดันที่ eardrum อันที่จริง ความถี่ 20 Hz ใกล้เคียงกับความถี่ต่ำสุดที่ทำให้เรารับรู้ pitch ของ complex sound
มีรายงานมานานนมแล้วว่า absolute threshold ของเสียงขึ้นอยู่กับช่วงเวลาที่เสียงปรากฏ กรณีที่ช่วงเวลาต่ำกว่า 200 ms เราต้องใช้เสียงที่ดังขึ้นเมื่อช่วงเวลาลดลงเพื่อให้ตรวจจับเสียงนั้นได้ มีนักวิทยาศาสตร์หลายคนสนใจศึกษาดูความสัมพันธ์ระหว่าง threshold กับ ช่วงเวลา งานยุคแรก ของ Hughes (1946) และ Garner กับ Miller (1947) บอกว่า ในช่วงเวลาที่เหมาะสมค่าหนึ่งนั้น ดูเหมือนหูของคนเราจะรวม (integrate) พลังงานของตัวกระตุ้นตลอดช่วงเวลาดังกล่าวเพื่อใช้ตรวจจับ tone สั้น ๆ อันนั้น ถ้าคำอธิบายนี้เป็นจริงนะครับ เราจะต้องได้ว่า I x t = ค่าคงที่ เมื่อ I คือ ความเข้มเสียงขีดเริ่มสำหรับโทนที่ปรากฏในช่วงเวลา t (นั่นคือ ถ้า t ลดลง, เราจะต้องวัดได้ I มากขึ้น) ซึ่งคำว่าค่าคงที่นี้ก็เป็นค่าคงที่ที่ขึ้นอยู่กับ (หรือแปรเปลี่ยนไปตาม) ความถี่
ในทางปฏิบัติ ผลลัพธ์จะเข้ากับความสัมพันธ์ (I - IL) x t = IL x τ = ค่าคงที่ มากกว่า เมื่อ IL คือ ความเข้มขีดเริ่มของโทนกรณีที่มีช่วงเวลายาว Garner กับ Miller ตีความว่าเฉพาะความเข้มที่เกิน IL เท่านั้นที่ถูกหูเอามารวมอย่างเป็นเชิงเส้น ในงานศึกษาต่อมาโดย Zwislocki (1960) Penner (1972) บอกว่า ความคิดดังกล่าวน่าจะผิด คือ auditory system ไม่น่าจะเป็นตัวรวมพลังงานกระตุ้น น่าจะเป็นกิจกรรมของนิวรอนมากกว่า และอาจเป็นไปได้ว่าที่ auditory system ตรวจจับ threshold ได้ดีกว่าเมื่อเสียงยาวกว่า เป็นเพราะเสียงที่ยาวกว่าเพิ่มโอกาสการตรวจจับซึ่งอาจเป็นแบบไม่ต่อเนื่องได้มากกว่า ไอเดียอันนี้เรียกว่า multiple looks และได้รับการสนับสนุนจากผลการทดลองของ Viemeister กับ Wakefield (1991)
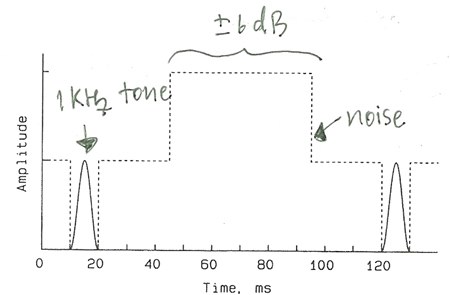
พวกเขาศึกษาการตรวจจับโทน 1 kHz สั้น ๆ ที่ปรากฏ ณ ช่วงเวลาที่ 10-20 ms และ/หรือ 120-130 ms (ตามรูปข้างบน) โดยเส้นประคือ noise ที่ช่วงเวลา 50 ms ตรงกลางนั้น ระดับของมันจะเปลี่ยนแปลงในช่วง ±6 dB ของแต่ละรอบการทดลอง พบว่า กรณีที่มีโทน 2 โทน ขีดเริ่มการได้ยินจะต่ำกว่ากรณีมีโทนเดียว (โทนตัวหน้าหรือตัวหลัง ตัวใดตัวหนึ่ง) ประมาณ 2.5 dB, ถ้า auditory system รวมพลังงานของโทน 2 โทนแบบต่อเนื่องตามที่การศึกษายุคแรก ๆ เสนอ ขีดเริ่มการได้ยินก็ต้องได้รับผลกระทบจากการเปลี่ยนระดับของ noise ตรงกลาง แต่ผลการทดลองกลับพบว่าขีดเริ่มของการได้ยินไม่แปรตามระดับของ noise ตรงกลาง ทฤษฎี temporal integration ที่ว่า (I - IL) x t เป็นค่าคงที่จึงให้คำอธิบายดี ๆ ต่อผลการทดลองนี้ไม่ได้นะครับ
ที่มา: บางส่วนจากบทที่ 2 Absolute Thresholds หนังสือ An Introduction to the Psychology of Hearing (6th Ed) โดย Brian C. J. Moore (Emerald, 2012)
| Create Date : 24 สิงหาคม 2556 | | |
| Last Update : 24 สิงหาคม 2556 10:59:49 น. |
| Counter : 3251 Pageviews. |
| |
|
| |
|
|
|
Subjective Attributes of Sound
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
ปกติเวลาพูดถึงเสียง โดยเฉพาะเสียงดนตรี เรามักจะบรรยายเสียงด้วยสมบัติ (attribute) หรือปริมาณ 4 อย่าง ได้แก่ ความดัง (loudness) pitch (ระดับเสียง, คนละอย่างกับระดับเสียงในความหมาย sound level นะครับ, ศัพท์บัญญัติราชบัณฑิตยสถาน บัญญัติ pitch = ระดับเสียง ในกลุ่มศัพท์สัทศาสตร์ ซึ่งจะหมายถึงเสียงสูง เสียงต่ำ อันนี้สัมพันธ์กับปริมาณทางกายภาพคือความถี่ แต่ sound level เป็นการวัดความดันหรือความเข้มเสียง, ในบล็อกกลุ่มนี้ ผมใช้คำว่า ระดับเสียง = sound level ฉะนั้นเวลาพูดถึง pitch จึงใช้ว่า พิตช์ จะไม่ใช้คำว่าระดับเสียงตามศัพท์บัญญัติ ซึ่งอาจจะทำให้งง), timbre (แทมเบ้อ, น้ำเสียงในความหมายคุณภาพเสียงที่ทำให้เสียงแตกต่างกันในแต่ละคนหรือแต่ละเครื่องดนตรี) และ ช่วงเวลาสั้น-ยาว (duration)
สมบัติหรือปริมาณทั้ง 4 ตัวนี้เป็นปริมาณเชิงจิตวิสัย (subjective) ที่ขึ้นอยู่กับปริมาณทางกายภาพที่สามารถวัดได้เชิงวัตถุวิสัย ขึ้นอยู่กับอะไรมากน้อยแค่ไหนนั้นแสดงดังตารางด้านล่างนี้ ยิ่ง "+" มาก ก็หมายถึง ปริมาณเชิงจิตวิสัยตัวนั้นขึ้นอยู่กับปริมาณเชิงวัตถุวิสัยมาก

(หมายเหตุ เนื้อหาเรียบเรียงจากบางส่วนของ 5.8 Subjective Attributes of Sound, The Science of Sound 3rd Ed, โดย Rossing, Moore, กับ Wheeler)
| Create Date : 24 สิงหาคม 2556 | | |
| Last Update : 24 สิงหาคม 2556 9:41:25 น. |
| Counter : 1116 Pageviews. |
| |
|
| |
|
|
|
Orthogonality
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เป็นอีกหนึ่ง concept ที่ใช้บ่อยใน DSP, คำว่า orthos ภาษากรีก หมายถึง ตั้งฉาก หรือ มุมฉาก, ในทางคณิตศาสตร์ เวกเตอร์ชนิดแถว a กับ b จะตั้งฉากกันเมื่อ inner product a*b′ = 0 ดังรูป
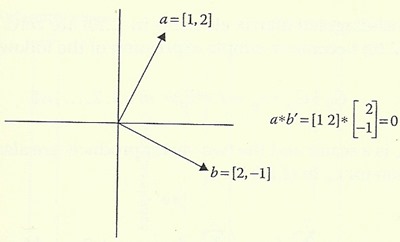
ถ้าเรามีแซมเปิ้ลอยู่ N แซมเปิ้ลจากฟังก์ชั่น 2 ฟังก์ชั่น a(t) กับ b(t) ที่ถูกสุ่มตัวอย่างที่ t = 0, T, ..., (N-1)T เพื่อสร้างเวกเตอร์ [a0 a1 ··· aN-1] กับ [b0 b1 ··· bN-1] เงื่อนไขสำหรับ orthogonality ในบริบทของแซมเปิ้ล N ตัวนี้คือ
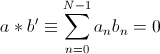
เช่น an = sin(2πn/N) และ bn = cos(2πn/N) เป็นฟังก์ชั่นที่ตั้งฉากกันภายใต้เงื่อนไขว่าเวกเตอร์ทั้งสองมี elements ที่ถูกสุ่มด้วย step คงที่ T แบบเดียวกัน และการที่เรารู้ว่าฟังก์ชั่นไหนตั้งฉากกันนั้นมีประโยชน์นะครับ อย่างในการหา least-squares coefficient ถ้า approximating function f̂(c,nT) ประกอบด้วยฟังก์ชั่น gm จำนวน M ฟังก์ชั่นที่ตั้งฉากกันและกัน การคำนวณก็จะง่ายขึ้น
ที่มา: หัวข้อ 2.3 Orthogonality หนังสือ Digital Signal Processing with Examples in MATLAB ของ S. D. Stearns กับ D. R. Hush
| Create Date : 28 กรกฎาคม 2556 | | |
| Last Update : 28 กรกฎาคม 2556 20:08:32 น. |
| Counter : 1573 Pageviews. |
| |
|
| |
|
|
|
|

