• ก็อยากจะเล่า
• หนังสือแนะนำ
• เกี่ยวกับศาสนา
• เรื่องที่น่าสนใจ
• หมากกระดาน
• อยากให้ลองฟัง
• ดูได้เรื่อยเรื่อย
• ห้องทดลองเขียน
• อิเล็กทรอนิกส์
• ภาษาต่างประเทศ
• ผู้คนที่น่าสนใจ
• matlab กับ [..]
• ในห้องของศล
• คลังวีดีโอคลิป
• เรื่องที่กำลังศึกษา

• Webmaster - BlogGang

• Deutsch-Englisch
• Latin Dictionary
• Babel Fish Translation
• พจนานุกรม
• Dictionary.com
• พจนานุกรมพุทธศาสน์
• CAMBRIDGE Dict.
• ศัพท์บัญญัติ
• วัดญาณเวศกวัน
• Oxford AL Dict.
• AT&T Natural Voices
• WordNet Online
• Etymology
• Catholic Encyclopedia
• Wolfram Alpha
• BlogGang.com

Pitch and Periodicity Coding [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 7 ในชื่อเดียวกัน หนังสือ The Sense of Hearing โดย Christopher J. Plack รายละเอียดบทที่ 2 - 6 ดูได้จากสารบัญกลุ่มเรื่องที่กำลังศึกษาตามลิงค์ข้างบนครับ ประเด็นของบทนี้ คือ ระบบการรับรู้เสียงสามารถนำเสนอและดึงข้อมูลเกี่ยวกับภาวะเป็นคาบ (periodicity) ของเสียงได้อย่างไร ซึ่งการรับรู้ภาวะเป็นคาบของเสียงนี่นะครับ จะสัมพันธ์กับปริมาณตัวหนึ่งที่เรียกว่า pitch ทำนองเดียวกับคู่ ความดัน-ความดัง ความดันเป็นปริมาณทางกายภาพที่สัมพันธ์กับความดังซึ่งเป็นปริมาณที่เรารับรู้ได้เมื่อเราได้ยินเสียง เป็น subjective และคู่ของ pitch ที่เป็นปริมาณทางกายภาพก็คือ ความถี่ Pitch ตอนที่เราได้ยินเสียงซึ่งมีความถี่มูลฐาน (fundamental frequency) ค่าใดค่าหนึ่ง เราอาจจะรับรู้ถึง pitch ที่สัมพันธ์กับความถี่มูลฐานนั้น นั่นคือ ระบบจะต้องมีความสามารถในการระบุความถี่มูลฐานของเสียง นิยามของ pitch ที่ผู้เขียนใช้นะครับ pitch เป็นลักษณะของการรับรู้เสียงที่ความแตกต่างของมันสัมพันธ์กับทำนองเพลง พูดอีกอย่างหนึ่งว่า เสียงใดก็ตามที่ให้การรับรู้เกี่ยวกับ pitch (หรือ เสียงใดก็ตามที่เรารับรู้ pitch ได้) เสียงนั้น ก็สามารถนำไปใช้สร้างทำนองเพลงได้โดยเปลี่ยนอัตราการซ้ำคาบของเสียง แต่ถ้าเสียงไม่ทำให้เกิดการรับรู้ pitch เราก็เอาเสียงนั้นไปทำเป็นทำนองเพลงไม่ได้ เช่น คุณไม่สามารถใช้เสียงที่ความถี่สูงกว่า 5 kHz หรือต่ำกว่า 25 Hz ไปสร้างทำนองเพลงได้ ก็แปลว่า เสียงในช่วง 25 Hz ถึง 5 kHz เท่านั้นที่ทำให้เกิด pitch ส่วนเสียงที่มีความถี่อยู่นอกช่วงนี้ ไม่ทำให้เกิดการรับรู้ pitch รูปด้านล่างแสดง waveform กับสเปกตรัมของเสียง 3 เสียง เสียงแรก บนสุดเป็น pure tone เสียงที่สองกับสามเป็น complex tone ทั้งสามเสียงมี pitch เดียวกัน เพราะทั้งสามเสียงมีความถี่มูลฐานเดียวกัน (ความถี่มูลฐานเป็นตัวกำหนด pitch) ความถี่มูลฐานของ pure tone คือ ความถี่ของ pure tone สำหรับความถี่มูลฐานของ complex tone คืออัตราการซ้ำคาบของ waveform คำถามต่อมา ความถี่สูงสุดและต่ำสุด (หรือความถี่มูลฐานสูงสุดและต่ำสุด) เท่าไรที่สามารถทำให้เกิด pitch ในกรณีของ pure tone มีการศึกษาของ Attneatve กับ Olson (1971) พบว่า ความถี่ที่สูงกว่า 4 kHz - 5 kHz ไม่สามารถนำมาสร้างทำนองเพลงได้ และนี่ก็เป็นค่าสูงสุดของความถี่มูลฐานของ complex tone ที่สามารถทำให้เกิด pitch ได้เช่นกันในกรณีที่มันมีฮาร์มอนิกแรกชัดเจน ซึ่งค่าดังกล่าวก็สอดคล้องกับโน้ตเสียงสูงสุด (เสียงแหลม) ที่วงออร์เคสตร้าสามารถเล่นได้ด้วย piccolo คือประมาณ 4.5 kHz และทำนองเพลงที่ใช้โน้ตความถี่สูงกว่านี้เล่นจะฟังประหลาด ๆ คุณสามารถบอกได้นะครับว่าเสียงมันเปลี่ยนแปลง แต่มันไม่เปลี่ยนแปลงในแบบที่ทำให้เป็นเพลง ถึงแม้ฮาร์มอนิกแรกของ complex tone ไม่มีในเสียง แต่เสียงนั้นก็สามารถทำให้เกิด pitch ได้ และช่วงของความถี่มูลฐานที่ทำให้เกิด pitch ขึ้นอยู่กับฮาร์มอนิกที่มีอยู่ในเสียง Ritsma (1962) แสดงให้เห็นว่า กรณีที่ความถี่มูลฐานเท่ากับ 100 Hz การใช้ complex tone ที่มีฮาร์มอนิกแค่ 3 ตัวต่อกัน ไม่สามารถทำให้เกิด pitch ได้เมื่อใช้ฮาร์มอนิกตัวที่สูงกว่าตัวที่ 25 แต่สำหรับเสียงที่มีความถี่มูลฐาน 500 Hz ขีดจำกัดบนจะอยู่ประมาณฮาร์มอนิกตัวที่ 10 ทางด้านความถี่ต่ำ พบว่า สำหรับ broadband complex tone ที่มีฮาร์มอนิกตั้งแต่ตัวแรกเป็นต้นไป สามารถนำไปเล่นทำนองเพลงได้ที่ความถี่มูลฐาน 30 Hz ซึ่งก็ใกล้เคียงกับโน้ตต้ำสุด (เสียงทุ้ม) ของเปียโน 27.5 Hz สรุป เสียงในช่วงความถี่ 30 - 5 kHz ทำให้เกิด pitch How Is Periodicity Represented? ในการตอบสนองต่อ pure tone นั้น firing rate ของนิวรอนขึ้นอยู่กับระดับของ pure tone ยิ่งระดับเสียงสูง firing rate ก็ยิ่งสูง (จนกว่าจะอิ่มตัว) และยังขึ้นอยู่กับความถี่ของ pure tone ยิ่งความถี่ใกล้กับความถี่ลักษณะเฉพาะของนิวรอน firing rate ก็ยิ่งสูง นั่นคือ firing rate ของนิวรอนในเส้นประสาทรับรู้เสียง เป็นตัวให้ข้อมูลเกี่ยวกับความถี่ของ pure tone และความถี่ลักษณะเฉพาะของนิวรอนตัวที่สร้าง spike มากสุด ก็ควรจะเท่ากับความถี่ของ tone (อย่างน้อยก็ที่ระดับเสียงต่ำ) นอกจากนี้ ความถี่ยังอาจถูกนำเสนอผ่านรูปแบบ (pattern) ของกิจกรรมของทุกนิวรอนที่มีความถี่ลักษณะเฉพาะแตกต่างกัน รูปต่อไปนี้แสดง excitation pattern ของนิวรอนชนิดเส้นใยมี spontaneous rate สูง ของ pure tone สองตัวที่มีความถี่ต่างกัน 10% 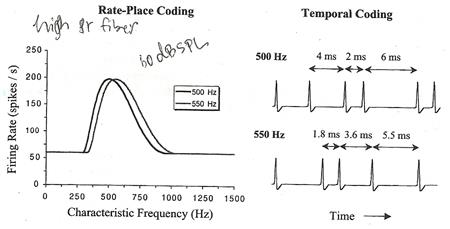เห็นว่า ความแตกต่างระหว่างสองเสียงนี้ไม่ได้ถูกนำเสนอด้วยตำแหน่งจุดสูงสุดของ excitation pattern เท่านั้น แต่ firing rate ที่ความถี่ลักษณะเฉพาะใด ๆ ก็ต่างกันด้วย สำหรับภาพด้านขวาแสดงให้เห็นผลจากความโน้มเอียงของนิวรอนที่จะล็อคกับเฟสเฉพาะบางเฟสต่อการสั่นของ basilar membrane นั่นคือ ตอนที่ถูกกระตุ้นโดย pure tone นิวรอนจะผลิต spike ที่บางเฟสของ waveform ทำให้ ช่วงระหว่าง spike ประมาณเป็นจำนวนเต็มเท่าของคาบของ pure tone ฉะนั้น ความถี่ที่แตกต่างกัน ย่อมทำให้รูปแบบของ spike ในโดเมนเวลาแตกต่างกัน เช่น กรณี pure tone ความถี่ 500 Hz (คาบ = 1/500 = 2 ms) ระยะห่างระหว่าง spike มีแนวโน้มที่จะเท่ากับ 2, 4, 6, ... ms ส่วน pure tone 550 Hz (คาบ = 1.8 ms) ระยะห่างระหว่าง spike มีแนวโน้มที่จะเท่ากับ 1.8, 3.6, 5.5, ... ms (ดูรูปบนขวา) ซึ่งการล็อคเฟสนี้จะเกิดขึ้นกับนิวรอนที่ตอบสนองต่อโทนไม่ว่าจะเป็นนิวรอนตัวใดก็ตาม และถึงแม้มันจะอิ่มตัวแล้ว แต่เฟสก็ยังคงล็อคอยู่ ถึงตอนนี้เราก็พูดได้ว่า ความถี่ของ pure tone ถูกแสดงด้วย (1) รูปแบบของกิจกรรมของนิวรอนที่มีความถี่ลักษณะเฉพาะต่าง ๆ กันทั้งหมด และ (2) รูปแบบของกิจกรรมของนิวรอนในโดเมนความเวลา คำถามคือ ข้อมูลแบบ (1) หรือ (2) ที่สมองนำไปตีความเพื่อทำให้เกิดการรับรู้ pitch? ยังไม่มีคำตอบเอกฉันท์นะครับ แต่มีข้อเท็จจริงบางอย่างที่อาจช่วยในการหาคำตอบได้ หนึ่ง, ความสามารถในการแยกความถี่ของ pure tone สองตัวที่ความถี่ต่ำกว่า 4 kHz ของคนเรานั้น เราสามารถทำได้ดีมาก ประณีตมาก ละเอียดกว่าที่จะอธิบายได้ด้วยการเปลี่ยนแปลงของ excitation pattern รูปต่อไปนี้แสดงการแยกความถี่ของ pure tone (ที่มีความยาว 200 ms) ในโดเมนความถี่ เห็นว่า เราสามารถตรวจจับความแตกต่างระหว่าง pure tone ความถี่ 1000 Hz กับ 1002 Hz ได้ สอง, phase locking จะเริ่มล้มเหลวหรือไม่ล็อคที่ความถี่ 5 kHz ซึ่งมันช่างพ้องกันพอดีกับที่เราเริ่มไม่รับรู้ pitch ข้อเท็จจริงทั้งสอง ทำให้ผู้เขียนเชื่อว่า phase locking หรือ temporal coding หรือ ข้อ (2) เป็นส่วนจำเป็นสำหรับการรับรู้ pitch รูปด้านล่าง บน แสดงสเปกตรัมของ complex tone ซึ่งเป็นเสียง input, สเปกตรัมทั้งหมดของ input มีแอมปลิจูดเท่ากัน และเป็น complex tone ที่มีความถี่มูลฐานเท่ากับ 100 Hz, รูปกลาง แสดง excitation pattern และ รูปล่าง แสดงการจำลองการสั่นของ basilar membrane ที่ 5 ตำแหน่งที่มีความถี่ลักษณะเฉพาะต่างกัน (ชี้โดยลูกศร) และด้านขวามือของรูปล่างคือ waveform ของ complex tone สังเกต ยิ่งความถี่สูง bandwidth ของฟิลเตอร์ก็ยิ่งกว้าง ดังนั้น มีเฉพาะฮาร์มอนิกต่ำ ๆ ไม่กี่ตัวแรกเท่านั้นที่ทำให้กราฟ excitation pattern มีลักษณะเป็นลูกคลื่นกระโดดแยกออกมา หมายความว่า เราสามารถได้ยินเสียงฮาร์มอนิกส์ 4-5 ตัวแรกนี้ของ complex tone แยกออกมาราวกับฮาร์มอนิกเหล่านั้นเป็น pure tone ได้ ส่วนที่ฮาร์มอนิกสูง ๆ หรือที่ความถี่กลางของฟิลเตอร์สูง ๆ นั้น excitation pattern ราบเรียบ (เพราะฟิลเตอร์ยอมให้ฮาร์มอนิกหลายตัวผ่านไปโดยไม่ลดทอนแอมปลิจูด เนื่องจาก bandwidth ของฟิลเตอร์กว้าง) นั่นคือ ฮาร์มอนิกสูง ๆ (สูงกว่าฮาร์มอนิกที่ 10) จะไม่ถูกแยกออกมา สรุปง่าย ๆ ว่า เมื่อดูจากการสั่นของ basilar membrane มันสามารถสั่นแยกฮาร์มอนิกต่ำได้ แต่แยกฮาร์มอนิกสูงไม่ได้ Plack กับ Oxenham (2005) บอกว่า cochlea สามารถแยกฮาร์มอนิก 8 ตัวแรกได้ โดยแทบไม่ขึ้นอยู่กับความถี่มูลฐาน แต่อย่างไรก็ตาม จำนวนของฮาร์มอนิกสูงสุดที่สามารถแยกได้จะลดลงที่ความถี่มูลฐานต่ำ (ต่ำกว่า 100 Hz) เนื่องจาก Q ของฟิลเตอร์มีค่าน้อยที่ความถี่กลางมีค่าต่ำ ข้อมูลเกี่ยวกับฮาร์มอนิกที่แยกออกมาแต่ละตัวจะถูกเก็บไว้ในเส้นประสาททั้งในรูปของ rate-place coding และ temporal coding ซึ่งข้อมูลเกี่ยวกับความถี่มูลฐานนั้น เราพึ่ง rate-place coding ไม่ได้มาก แต่ข้อมูลดังกล่าวมีอยู่ใน temporal coding จากการศึกษาของ Jorin กับ Yin (1992) พบว่า นิวรอนมีแนวโน้มที่จะล็อคเฟสกับ envelope ของการสั่นของ basilar membrane ดังนั้น ช่วงเวลาห่างระหว่าง spike จึงมีแนวโน้มที่จะเป็นจำนวนเต็มเท่าของของคาบของ complex tone เนื่องจาก คนเราสามารถแยกความแตกต่างของความถี่มูลฐานได้ดีมาก (ต่ำกว่า 1% สำหรับฮาร์มอนิกแยก เราก็ยังสามารถแยกความแตกต่างได้) จึงเชื่อกันว่า temporal coding เป็นตัวสำคัญในการส่งข้อมูลความถี่มูลฐาน รูปนี้แสดงการสั่นของ basilar membrane กับรูปแบบ spike ในการตอบสนองต่อฮาร์มอนิกที่แยกออกมาตัวหนึ่ง (รูปซ้าย) กับฮาร์มอนิกหลาย ๆ ตัวที่ไม่แยกออกมา (รูปขวา) เห็นว่า เส้นใยประสาทที่จูนกับฮาร์มอนิกตัวที่แยก จะล็อกเฟสกับโครงสร้างละเอียด ขณะที่เส้นใยที่จูนกับฮาร์มอนิกที่ไม่แยก จะล็อคเฟสกับ envelope How Is Periodicity Extracted? คำถาม ระบบรับรู้เสียงนำข้อมูลในเส้นประสาทมาใช้อย่างไร ด้วยวิธีการใด เพื่อที่จะหา periodicity ของเสียง และทำให้เรารับรู้ pitch? เมื่อก่อน Ohm (1843) กับ Helmholtz (1863) คิดว่า pitch ของ complex tone ถูกกำหนดโดยความถี่ของฮาร์มอนิกแรก พวกเขาคิดว่า ถ้าเราได้ยินองค์ประกอบความถี่เสียงหลาย ๆ ตัว เราก็แค่ดึงความถี่ขององค์ประกอบต่ำสุดออกมา อันนั้นแหละคือความถี่มูลฐานและ periodicity ซึ่งในชีวิตประจำวันทั่ว ๆ ไป ไอเดียนี้ถูกต้องนะครับ ความถี่มูลฐานเท่ากับความถี่ของฮาร์มอนิกแรก แต่ในปี 1956 Licklider ได้แสดงให้เห็นว่า ถึงแม้เราจะเพิ่ม low-pass noise เพื่อทำการ mask ย่านความถี่บริเวณความถี่มูลฐานของ complex tone เราก็ยังคงได้รับรู้ pitch ได้เหมือนกับกรณีที่ไม่เติม noise ลงไป หมายความว่า ถึงแม้เราจะไม่ได้ยินองค์ประกอบมูลฐาน แต่ pitch ซึ่งสัมพันธ์กับ periodicity ของ complex tone ก็ไม่เปลี่ยนแปลง เท่ากับ ระบบรับรู้เสียงจะต้องสามารถดึงข้อมูลเกี่ยวกับความถี่มูลฐานจากฮาร์มอนิกที่สูงกว่าได้ ถึงแม้ฮาร์มอนิกแรกจะไม่จำเป็นต่อการรับรู้ pitch แต่ก็มีบริเวณหรือย่านฮาร์มอนิกลำดับต่ำ ๆ ที่สำคัญต่อการรับรู้ pitch ตัวอย่างจากการทดลองหนึ่งของ Moore, Glasberg กับ Peters (1985) ซึ่งได้เปลี่ยนความถี่ของฮาร์มอนิกตัวหนึ่งใน complex tone ดังรูป เห็นว่า การเปลี่ยนความถี่ของฮาร์มอนิก ทำให้ pitch เปลี่ยน โดยตัวเลขขวามือของกราฟคือหมายเลขฮาร์มอนิกที่เปลี่ยนความถี่ (เพียงเล็กน้อย) ดังกล่าว Moore และคณะพบว่า การเปลี่ยนฮาร์มอนิกที่สอง สาม และสี่ ส่งผลกระทบต่อความถี่มูลฐานในช่วง 100 - 400 Hz มากที่สุด สำหรับอีกการทดลองหนึ่ง Dai (2000) พบว่า ฮาร์มอนิกส์ที่มีความถี่ราว ๆ 600 Hz เป็นตัวสำคัญสุด ซึ่งจะเป็นฮาร์มอนิกตัวที่เท่าไรนั้นขึ้นอยู่กับความถี่มูลฐาน เช่น ถ้าความถี่มูลฐาน 100 Hz ฮาร์มอนิกตัวที่หกเป็นตัวสำคัญที่สุด แต่ถ้าความถี่มูลฐาน 200 Hz ฮาร์มอนิกตัวที่สามก็สำคัญสุด ไม่ว่าหมายเลขที่แน่นอนของฮาร์มอนิกที่สำคัญต่อการรับรู้ pitch จะเป็นเท่าไร แต่สิ่งหนึ่งที่งานวิจัยทั้งหมดเห็นพ้องต้องกันคือ ฮาร์มอนิกที่แยกออกมา เป็นส่วนสำคัญที่สุดต่อการรับรู้ pitch หมายความว่า ถ้า complex tone ไม่มีฮาร์มอนิกที่สามารถแยกออกมาได้ ถึงแม้ complex tone ตัวนั้นอาจจะเอาไปสร้างทำนองเพลงได้ แต่มันจะให้ pitch ที่อ่อนมาก ไม่ชัดเจน นอกจากนี้ เรายังสามารถแยกความแตกต่างระหว่างความถี่มูลฐานของกลุ่มที่ประกอบด้วยฮาร์มอนิกแยก ได้ดีกว่าการแยกความแตกต่างระหว่างความถี่มูลฐานของกลุ่มที่ไม่มีฮาร์มอนิกแยก ดังรูป จากรูป F0DL = fundamental frequency difference limen แกนตั้งเป็นความแตกต่างต่ำสุดในความถี่มูลฐานที่สามารถตรวจจับได้ โดยเสียงที่นำมาเปรียบเทียบแต่ละกลุ่มจะมีฮาร์มอนิก 11 ตัวต่อเนื่องกัน เห็นว่า ความสามารถในการตรวจจับความต่างแย่ลงตั้งแต่กลุ่มที่มีหมายเลขฮาร์มอนิกเท่ากับสิบเป็นฮาร์มอนิกต่ำสุดเป็นต้นไป คำถามต่อมา ระบบรับรู้เสียงใช้วิธีการใดในการหาความถี่มูลฐานของ complex tone? ตอนนี้มีโมเดลที่เสนอว่าอาจจะเป็นคำตอบอยู่ 2 โมเดล คือ pattern-recognition model กับ temporal model ไอเดียของ pattern recognition คือ ระบบรับรู้เสียงสามารถใช้ pattern ของความถี่ฮาร์มอนิกในการประมาณความถี่มูลฐาน เช่น ถ้ามีฮาร์มอนิกที่มีความถี่ 400, 600 กับ 800 Hz เราก็จะรู้ว่าเสียงดังกล่าวมีความถี่มูลฐาน 200 Hz หรือถ้ามีฮาร์มอนิก 750, 1250 กับ 1500 เราก็รู้ว่าความถี่มูลฐานเท่ากับ 250 Hz ทั้งนี้เพราะระยะห่างระหว่างฮาร์มอนิกที่ติดกันจะเท่ากับความถี่มูลฐาน ฉะนั้นใช้ฮาร์มอนิกต่ำ ๆ ที่แยกออกมาแค่สองตัวก็เพียงพอแล้วสำหรับการรับรู้ pitch ในการทำ pattern recognition ก็มีข้อเสนอว่าคงจะมี harmonic template ดังรูปด้านล่าง สำหรับโมเดลนี้ อันดับแรก ระบบจะต้องแยกฮาร์มอนิกต่ำ ๆ ที่เป็นฮาร์มอนิกแยกออกมาก่อน แล้วดูว่าฮาร์มอนิกแยกเหล่านั้นเข้ากันกับ template อันไหนมากที่สุด ปัญหาของโมเดลนี้คือ มันไม่สามารถใช้อธิบายการรับรู้ pitch ของเสียงที่ไม่มีฮาร์มอนิกแยกได้ อีกโมเดลหนึ่ง temporal model หาความถี่มูลฐานจากการดูรูปแบบ spike ในเส้นประสาททั้งจากฮาร์มอนิกแยกและไม่แยก ดังรูป รูปแสดงการสั่นของ basilar membrane และ phase locking ในเส้นประสาทที่ตอบสนองต่อฮาร์มอนิกที่หนึ่ง สอง สี่ หก และที่ความถี่ 1600 Hz (มีหลายฮาร์มอนิกไม่แยก) ไอเดียของโมเดลนี้คือ จะต้องมีระยะห่างระหว่าง spike สองตัวใด ๆ (เรียกว่า inter-spike interval) ในแต่ละเส้นใยที่สะท้อนถึงความถี่มูลฐานของเสียง (แสดงคาบด้วยลูกศร) และวิธีที่มีประสิทธิภาพในการหาคาบดังกล่าว เริ่มต้นด้วยการทำ autocorrelation หรือเปรียบเทียบสัญญาณใด ๆ กับสัญญาณหน่วงเวลา (ที่ค่าเวลาหน่วงต่าง ๆ กัน) ของตัวมันเอง ดังรูป จะเห็นได้ว่า ที่เวลาหน่วงเท่ากับจำนวนเต็มเท่าของอัตราซ้ำคาบของ waveform นั้น correlation strength (หาจาก ผลรวมของผลคูณระหว่างสัญญาณต้นฉบับกับสัญญาณหน่วงเวลา ณ เวลาใด ๆ) จะมีค่าสูง หลังจากนั้น ให้เอาผลลัพธ์จาก autocorrelation แต่ละเส้น ทุกเส้น มารวมกันตรง ๆ เพื่อหาคาบร่วม ซึ่งคาบร่วมตัวนี้แหละครับเป็นส่วนกลับของความถี่มูลฐาน ข้อด้อยของโมเดลนี้คือ มันใช้อธิบายไม่ได้ว่า ทำไมเราสามารถแยกความแตกต่างของความถี่มูลฐานได้ดี และทำไม pitch ถึงมีความชัดเจนกว่าในเสียงที่มีฮาร์มอนิกแยกเมื่อเทียบกับเสียงที่ไม่มีฮาร์มอนิกแยก ข้อด้อยอีกประการมาจากการทดลองเอาพัลซ์บางตัวออกในแบบที่ไม่กระทบกับผลจาก autocorrelation ซึ่งหมายความว่า โมเดลนี้จะให้ความถี่มูลฐานเท่าเดิม ขัดกับผลการทดลองที่ผู้ฟังได้ยิน pitch ลดลง ข้อเสนอคือ เป็นไปได้ที่จะมีกลไกแยกต่างหากจากกันสำหรับฮาร์มอนิกแยกและฮาร์มอนิกไม่แยก โมเดล pattern recognition จึงยังมีโอกาสถูก แม้มันจะอธิบายเสียงที่ไม่มีฮาร์มอนิกแยกไม่ได้ นี่ยังเป็นเรื่องที่อยู่ในระหว่างการค้นคว้าครับ   Create Date : 20 พฤษภาคม 2556     Last Update : 23 สิงหาคม 2556 15:37:05 น. Counter : 3933 Pageviews.   0 comment Share Tweet

Loudness and Intensity Coding [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 6 ในชื่อเดียวกัน หนังสือ The Sense of Hearing โดย Christopher J. Plack รายละเอียดบทที่ 2 - 5 ดูได้จากสารบัญกลุ่มเรื่องที่กำลังศึกษาตามลิงค์ข้างบนครับ ลักษณะของเสียงถูกกำหนดโดยการเปลี่ยนแปลงความเข้ม (intensity) ในโดเมนความถี่และเวลา ด้วยเหตุนี้ เพื่อให้สามารถแยกแยะเสียงหนึ่งออกจากอีกเสียงหนึ่งได้ ระบบรับรู้เสียงของเราจะต้องมีวิธีแทนความเข้มเสียงในรูปการส่งสัญญาณไฟฟ้าในเส้นประสาท และมีวิธีเปรียบเทียบความเข้มนั้นในโดเมนความถี่และเวลา The Dynamic Range of Hearing dynamic range ของระบบใด ๆ คือช่วงหรือพิสัยของระดับต่าง ๆ ที่ระบบสามารถทำงานได้ dynamic range ของการได้ยินก็คือ ช่วงที่อยู่ระหว่างระดับเสียงต่ำสุดกับระดับเสียงสูงสุดที่เรายังสามารถประมวลเสียงได้อย่างมีประสิทธิภาพ ระดับเสียงต่ำสุดที่ผู้ฟังสามารถได้ยินในสภาพแวดล้อมที่ไม่มีเสียงอื่นรบกวน เรียกว่า absolute threshold (ขีดเริ่มสัมบูรณ์) รูป audiogram ด้านล่างนี้พล็อต absolute threshold เป็นฟังก์ชั่นของความถี่ของ pure tone จากรูป absolute threshold คือ เส้นหนาล่างสุด ความหมายของเส้นนี้คือ เราจะเริ่มได้ยินเสียง pure tone ที่ความถี่ใด ๆ ในสภาพแวดล้อมสงบ ก็ต่อเมื่อ pure tone นั้นมีระดับเสียงอย่างน้อยเท่ากับ absolute threshold เห็นว่า threshold มีค่าต่ำในช่วง 1000 - 6000 Hz หรือพูดอีกอย่างหนึ่งว่า ช่วงความถี่นี้เป็นช่วงที่เรามีความอ่อนไหว (sensitivity) ต่อเสียงมากที่สุด ซึ่งย่านอ่อนไหวดังกล่าวก็สะท้อนถึงเรโซแนนซ์ในหูชั้นนอกและชั้นกลาง และเสียงในย่านความถี่ 1 kHz - 6 kHz ก็สามารถถูกส่งผ่านให้กับ cochlea ได้อย่างมีประสิทธิภาพกว่าเสียงในย่านความถี่อื่น (และก็ไม่น่าแปลกใจที่เสียงพูดของคนเราจะอยู่ในย่านความถี่นี้แหละ) แต่ละเส้น audiogram แสดงถึงการเท่ากันของความดัง (loudness) ของทุกจุดบนเส้นนั้น และตัวเลขบนเส้นที่อยู่ในแนวดิ่งตรงกับ 1 kHz คือ ระดับเสียงของ pure tone ที่ความถี่ 1 kHz ช่วงความถี่ของการได้ยินในคน ประมาณ 20 Hz - 20 kHz (ค่าความถี่สูงสุดจะสูงกว่านี้ในสัตว์เลี้ยงลูกด้วยนมสายพันธุ์อื่น) และตรงบริเวณปลายสูงสุด-ต่ำสุดของความถี่ที่เราสามารถได้ยิน absolute threshold จะสูงกว่า 80 dB SPL รูปด้านบนไม่ได้แสดงระดับเสียงที่ความถี่มากกว่า 15 kHz แต่โปรดทราบว่า threshold จะเพิ่มขึ้นอย่างรวดเร็ว (ความชันมาก) ที่ความถี่มากกว่า 15 kHz ตอนนี้เราได้ระดับเสียงต่ำสุดแล้ว คือ absolute threshold มีค่าต่ำสุดประมาณ 0 dB SPL (หากยังจำได้ หน่วย dB SPL เราจงใจกำหนดความดันอ้างอิง = 0.00002 N/m2 เพราะอยากให้ 0 dB SPL มีค่าใกล้เคียงกับระดับเสียงต่ำสุดที่เราสามารถได้ยินที่ 1 kHz) คำถาม ระดับเสียงสูงสุดจะหายังไง? มี 2 วิธีครับ (1) ดูระดับที่เริ่มทำให้เจ็บปวด ถ้าเสียงมีระดับสูงกว่า 120 dB SPL เราจะเริ่มรู้สึกเจ็บปวดทางกายภาพ การฟังเสียงที่ระดับสูง ๆ นี้แม้เพียงช่วงเวลาสั้น ๆ ก็อาจทำลายหูได้อย่างถาวรนะครับ (2) ดูระดับที่เราเริ่มแยกเสียงสองเสียงไม่ออก เช่น สมมติเราสามารถฟังเสียง 140 dB SPL ได้ แต่เราฟังมันแล้วก็ไม่เห็นจะต่างจากเสียง 130 dB SPL จากการทดลอง (ซึ่งมีไม่มากนัก ด้วยเหตุผลทางศีลธรรม) พบว่าความสามารถในการตรวจจับความแตกต่างระหว่างระดับเสียงสองระดับ จะเริ่มลดลงเมื่อระดับเสียงสูงกว่า 100 dB SPL แต่ในงานศึกษาบางชิ้นก็ระบุว่า ยังมีความเป็นไปได้อยู่นะที่จะแยกความแตกต่างที่ระดับเสียงสูงถึง 120 dB SPL สรุปตอนนี้ ไม่ว่าจะใช้วิธีไหน เราก็ประเมินคร่าว ๆ ได้ว่าระดับเสียงสูงสุดอยู่ราว 120 dB SPL นั่นคือ dynamic range ของการได้ยินเท่ากับ 0 dB - 120 dB SPL ในย่านความถี่กลาง ๆ (1 kHz - 6 kHz) และ range ลดลงเมื่อความถี่สูงหรือต่ำกว่าย่านนี้ ถ้าดูความเข้มเสียงสูงสุดกับต่ำสุดนะครับ ตัวเลข 120 dB SPL บอกเราว่า ความเข้มเสียงสูงสุดสูงกว่าความเข้มเสียงต่ำสุดถึงหนึ่งล้านล้านเท่า! Loudness เราคุ้นเคยกับความดัง (loudness) กันบ่อยในชีวิตประจำวัน เช่น พูดว่า "นศ. ธรรมศาสตร์ใช้ห้องสมุดติวหนังสือกันเสียงดังเกินไป" ความดังคืออะไร? ความดัง สามารถนิยามได้ว่า เป็นปริมาณที่เกี่ยวข้องกับการรับรู้เสียงซึ่งมีความสัมพันธ์กับความเข้มเสียง ขอขยายความหน่อยนะครับ คำว่า "ปริมาณที่เกี่ยวข้องกับการรับรู้เสียง" แปลว่า ความดัง เป็น subjective ใช้คนเป็นตัววัด ซึ่งปริมาณตัวนี้จะมีความสัมพันธ์กับปริมาณทางกายภาพที่สามารถวัดได้ด้วยเครื่องมือ เช่น ความเข้มหรือความดัน ตัวอย่าง ถ้าผมเปิด volume เครื่องขยายเสียงขึ้น นั่นคือ ผมเพิ่มความเข้มเสียงทางกายภาพ และผมได้ยินเสียงดังขึ้น นี่คือปริมาณที่เกี่ยวกับการรับรู้ และเราจะไม่พูดว่า "เสียงนี้มีความดัง 50 dB SPL" เพราะ dB เป็นหน่วยของปริมาณทางกายภาพ ไม่ใช่หน่วยของขนาดเชิงอัตวิสัย ในเมื่อความดังเป็นตัวแปรที่เป็นอัตวิสัยหรือ subjective งั้นแปลว่ามันไม่สามารถวัดได้รึเปล่า? ไม่ใช่นะครับ เพราะ ถ้ามีใครมาบอกให้เราปรับเสียง 2 เสียงให้ดังเท่ากัน เราสามารถทำภารกิจนี้ได้ หมายความว่า เราสามารถวัดความดังของเสียงได้ ตัวอย่างเส้นใน audiogram รูปแรก ก็บอกว่าทุกจุดบนเส้นนั้นมีความดังเท่ากัน และบอกโดยเทียบกับความดังของ pure tone ความถี่ 1 kHz สังเกตว่า เส้นกราฟความดังเท่ากันจะตกท้องช้างตรงย่านความถี่กลาง ๆ เหมือนกราฟ absolute threshold (ซึ่งก็เป็นเส้นความดังเท่ากันเหมือนกัน, หรือจะพูดว่า เส้นที่ไม่ดังเท่ากันเหมือนกันก็ได้ เพราะมันเพิ่งเริ่มได้ยิน :P) และที่ระดับเสียงสูง ๆ กราฟก็เริ่มแบนมากขึ้น หมายความว่า ความดังไม่แปรตามความถี่เท่าไรนักที่ระดับเสียงสูง เราวัดระดับความดัง (loudness level) ของ pure tone ที่ความถี่ใด ๆ โดยปรับความดังของ tone ที่ความถี่ 1000 Hz ให้เท่ากับความดังของ tone ตัวที่เรากำลังจะหาความดัง แล้วดูระดับในหน่วย dB SPL ของ 1000-Hz pure tone ซึ่งระดับความดังนี้จะมีหน่วยเป็น phons เช่น ดูกราฟรูปแรก เห็นว่า pure tone ความถี่ 100 Hz ที่ 40 dB SPL มีความดังเท่ากับความดังของ 1000-Hz pure tone ที่ระดับเสียง 10 dB SPL เราจะพูดว่า pure tone 100 Hz 40 dB SPL มีความดัง 10 phons หรือพูดอีกอย่างหนึ่งว่า เส้นกราฟเส้นที่ 2 จากล่าง (เส้นที่มีเลข 10 กำกับ) คือ เส้นที่มีความดัง 10 phons ลองอีกสักตัวอย่างนะ เสียงใดก็ตามที่ดังเท่ากับ 1000-Hz pure tone ที่ระดับ 60 dB SPL จะมีความดัง 60 phons อันนี้คือการวัดระดับความดังด้วยการจับคู่ความดังที่เท่ากัน (loudness matching) loudness matching ยังสามารถใช้ในการดูผลกระทบของ bandwidth ที่มีต่อความดัง โดยการปรับระดับของเสียงที่ bandwidth คงที่จนกว่าจะได้ความดังเท่ากับเสียงที่ bandwidth ไม่คงที่ ผลลัพธ์ที่ได้คือ การเพิ่ม bandwidth ของ noise ที่ระดับเสียงรวมคงที่ (หมายความว่าระดับของสเปกตรัมลดลงเมื่อ bandwidth กว้างขึ้น) จะทำให้ความดังเพิ่มขึ้น เมื่อ bandwidth ของ noise นั้นกว้างกว่า bandwidth ของฟิลเตอร์ของระบบรับรู้เสียง และระดับของ noise เป็นระดับกลาง ๆ ดังรูป แต่หาก bandwidth ของ noise แคบกว่า bandwidth ของฟิลเตอร์ การเปลี่ยน bandwidth ของ noise จะส่งผลกระทบเพียงเล็กน้อยต่อความดังของเสียงที่ระดับรวมคงที่ ลองมองอีกมุมนะครับ ถ้ากำลังของเสียงถูกกระจายออกกินบริเวณกว้างของ cochlea จะทำให้ความดังเพิ่มขึ้น เพราะความดังไม่ได้ถูกกำหนดจากเพียงแค่ระดับเสียงเท่านั้น แต่ต้องดูการกระจายสเปกตรัมด้วย นอกจากนี้ loudness matching ยังใช้ดูผลกระทบของช่วงเวลาต่อความดังได้อีก โดยการเปลี่ยนระดับของเสียงที่กำหนดช่วงเวลาคงที่กระทั่งมันดังเท่ากับเสียงที่ช่วงเวลาไม่คงที่ พบว่า เสียงที่กินช่วงเวลานานกว่า จะดังกว่า นั่นคือ ที่ระดับเสียงกลาง ๆ pure tone ซึ่งมีช่วงเวลาสั้น ๆ จะต้องมีระดับเสียงสูงกว่า pure tone ที่มีช่วงเวลายาวกว่า เพื่อให้ pure tone ทั้งสองมีความดังเท่ากัน แต่ถ้าเป็นกรณีระดับเสียงสูงหรือต่ำ ความแตกต่างนี้จะลดลง เป็นไปได้ครับว่าผลกระทบที่ระดับเสียงกลาง ๆ ดังกล่าวสัมพันธ์กับการบีบอัดที่ระดับเสียงกลาง ๆ บน basilar membrane loudness matching อาจให้ข้อมูลสำคัญแก่เราในเรื่องผลกระทบต่อความดังอันเนื่องมาจากลักษณะบางอย่าง เช่น ความถี่ bandwidth หรือ ช่วงเวลา ของเสียง แต่กระนั้น loudness matching ก็ไม่อาจบอกเราได้ตรง ๆ ว่าความดังเปลี่ยนไปตามระดับเสียงอย่างไร พูดอีกอย่างว่า วิธี loudness matching ไม่ได้ให้ตัวเลขที่สัมพันธ์โดยตรงกับขนาดความรู้สึกของเรา วิธีหนึ่งที่เราอาจใช้วัดได้คือ เปิดเสียง 2 เสียง แล้วให้คนฟังป้อนค่าตัวเลขว่าเสียงที่ดังกว่านั้นดังกว่าเท่าไร หรือไม่อีกวิธี ก็ขอให้ผู้ฟังปรับเสียงหนึ่งจนกว่าจะดังเป็น 2 เท่า (หรือ x เท่า) ของอีกเสียงหนึ่ง วิธีการทั้งสองวิธีนี้มีชื่อเรียก magnitude estimation กับ magnitude production ตามลำดับ แล้วก็ใช้ได้ผลดี ทำให้เราได้กฎกำลังของ Steven (Steven's power law) บอกว่า           L = kIα เมื่อ L คือ ความดัง ในหน่วย sone, I คือ ความเข้มเสียง ในหน่วย W/m2 และ k เป็นค่าคงที่ ความดัง 1 sone นั้นนิยามเท่ากับความดังของเสียง pure tone ความถี่ 1 kHz ที่ระดับ 40 dB SPL ความดังของเสียงที่ดังกว่านี้ 4 เท่า เราจะพูดว่ามีความดัง 4 sones สำหรับเลขชี้กำลัง α มีค่าอยู่ระหว่าง 0.2 กับ 0.3 สำหรับเสียงระดับสูงกว่า 40 dB SPL และสำหรับความถี่มากกว่า 200 Hz แต่ในเสียงที่ระดับต่ำกว่า 40 dB SPL และสำหรับเสียงความถี่ต่ำกว่า 200 Hz นั้น ความดังจะเพิ่มขึ้นอย่างมากเมื่อความเข้มเพิ่ม (ค่า α สูงกว่า 0.3) รูปต่อไปนี้แสดงความดังที่เพิ่มขึ้นตามระดับเสียงของ 1000-Hz pure tone ฟังก์ชั่นที่แสดงความสัมพันธ์ระหว่างระดับเสียงกับความดังนั้น คล้ายกับฟังก์ชั่นแสดงความสัมพันธ์ระหว่างระดับเสียงกับอัตราเร็วของการเคลื่อนที่ของ basilar membrane กล่าวคือ ฟังก์ชั่นทั้งสองจะลึกชันที่ระดับเสียงต่ำมากกว่าที่ระดับเสียงสูงเมื่อพล็อตบนสเกล logarithm และจากการศึกษาของ Schlauch, DiGiovanni กับ Reis (1998) เราพูดได้ว่า ความดังแปรผันตามอัตราเร็วของ basilar membrane ยกกำลังสอง นอกจากนี้ เราสามารถใช้แบบจำลองความดัง (models of loudness) จาก excitation pattern มาอธิบายผลกระทบของระดับเสียงกับ bandwidth ได้ด้วย แบบจำลองจะคำนวณความดังจำเพาะ (specific loudness) ที่ output ของฟิลเตอร์แต่ละตัวในแต่ละย่านความถี่ ซึ่งก็คือความเข้มของสัญญาณ input ที่ถูกบีบอัดนั่นแหละ (เนื่องจากการบีบอัดบน basilar membrane) เราสามารถถือว่าความดังจำเพาะที่ความถี่ศูนย์กลางใด ๆ เป็นความดังที่ตำแหน่งซึ่งสัมพันธ์กันบน basilar membrane และเราหาความดังสุทธิของเสียงจากผลรวมของความดังจำเพาะตลอดความถี่กลางทั้งหมด เท่ากับ ความดังเป็นการวัดกิจกรรมทั้งหมดของ basilar membrane ข้างบนเป็นรูปแสดงความดังจำเพาะของ noise สองตัวที่มี bandwidth ต่างกัน แต่มีระดับเสียงโดยรวมเท่ากัน แบบจำลองความดังบอกว่า ความดังของเสียงเท่ากับพื้นที่ใต้กราฟรูปแบบความดังจำเพาะ ดังนั้น noise ที่แคบกว่าจะดังน้อยกว่า ถึงแม้ bandwidth กว้างกว่า 2 เท่าจะทำให้ความหนาแน่นสเปกตรัมลดลงครึ่งหนึ่ง แต่ความดังจำเพาะที่แต่ละความถี่กลางจะลดลงไม่มาก ทั้งนี้เพราะสมบัติบีบอัดของ cochlea สรุปนะครับ พลังงานของเสียงกระตุ้นที่แผ่กระจายครอบคลุมย่านความถี่กว้างกว่าหรือกินอาณาบริเวณของ cochlea มากกว่า จะทำให้ความดังเพิ่มขึ้น แบบจำลองความดังสามารถใช้ประมาณค่าความดังของเสียงใด ๆ ก็ได้ ความสำเร็จของแบบจำลองบอกเราเป็นนัยว่า การรับรู้ความดังของมนุษย์นั้น มาจากผลรวมของกิจกรรมของนิวรอนทั้งหมดในระบบรับรู้เสียง How is Intensity Represented in the Auditory System? สมบัติพื้นฐานประการหนึ่งของเส้นใยประสาทระบบรับรู้เสียงคือ firing rate จะเพิ่มขึ้นเมื่อระดับเสียงเพิ่มขึ้น ฉะนั้น คำตอบต่อคำถามหัวข้อนี้ก็ดูเหมือนไม่มีอะไร ข้อมูลเกี่ยวกับความเข้มเสียงถูกแทนหรือถูกนำเสนอโดย firing rate ของนิวรอน แต่ในความเป็นจริงมันไม่ง่ายแค่นี้นะสิ intensity discrimination (การแยกความเข้ม) หมายถึง ความสามารถของคนเราที่จะตรวจจับความแตกต่างระหว่างความเข้มของเสียงสองเสียง โดยทั่วไป เราจะทำการทดลองแบบนี้ครับ ให้ผู้ร่วมทดลองฟังเสียง 2 เสียงที่มีระยะห่างประมาณ 0.5 วินาที ดังรูป ผู้ฟังต้องตอบว่าเสียงไหนดังกว่ากัน จากนั้นทำซ้ำ โดยแต่ละรอบของการทำซ้ำให้ลด ΔI ลงเรื่อย ๆ จนกว่าผู้ฟังจะตอบถูกต่ำกว่าเกณฑ์ที่เรากำหนด เช่น กำหนดว่าต้องตอบถูก 71% เราก็จะได้ ΔI ต่ำสุดที่ทำให้ผู้ฟังตรวจจับความแตกต่างได้ ต่อไปเราเขียนแทน ΔI นะครับ ให้รู้กันว่าหมายถึง "ΔI ต่ำสุด" jnd หรือ just-noticeable difference ของความเข้มเสียงนิยมแสดงด้วย 2 แบบนี้ คือ เศษส่วนเวเบอร์ (Weber fraction) ในหน่วย dB กับ ΔL           Weber fraction = ΔI / I เมื่อ I คือความเข้มเสียงที่เป็น baseline (หรือ pedestal)           Weber fraction (ในหน่วย dB) = 10 × log10(ΔI / I) สมการนี้บอกเราว่า ถ้าคุณจำเป็นต้องเพิ่มความเข้มของเสียงขึ้นสองเท่าในการทำให้เราตรวจจับได้ว่าความดังของมันเปลี่ยน พูดอีกอย่างว่า นี่คือกรณีที่ ΔI = I ก็จะได้เศษส่วนเวเบอร์เท่ากับ 0 dB (เพราะ log 1 = 0) ถ้า jnd สัมพันธ์กับการเพิ่มความเข้มที่น้อยกว่าสองเท่า (ซึ่งก็คือกรณีที่ ΔI < I) เศษส่วนเวเบอร์ในหน่วย dB จะมีค่าติดลบ (เพราะ log10x < 0 เมื่อ 0 < x < 1) การแสดง jnd ด้วย ΔL           ΔL = 10 × log10[(ΔI + I) / I] สังเกตว่า ΔL จะไม่มีทางติดลบนะครับ เพราะ ΔI + I ≥ I เสมอ และในกรณีที่ jnd สูงมาก ๆ หรือ ΔI >> I เราก็จะได้ เศษส่วนเวเบอร์ ≈ ΔL คำถามสำคัญถัดมาคือ คนเรามีความสามารถแยกความเข้มเสียงได้ดีแค่ไหน? เศษส่วนเวเบอร์สำหรับ wideband white noise มีค่าประมาณ -10 dB (หรือ ΔL = 0.4 dB) และค่อนข้างคงที่ในโดเมนของระดับเสียง สำหรับช่วงระดับ 30 dB SPL ถึง 110 dB SPL แต่ถ้าระดับเสียงต่ำกว่า 30 dB SPL เศษส่วนเวเบอร์จะมีค่าสูงขึ้น (หมายความว่า ความสามารถในการแยกความเข้มต่ำลง) ดังรูป การที่เศษส่วนเวเบอร์มีค่าคงที่หมายความว่า ΔI แปรตาม I สมบัติอันนี้ ΔI ~ I เรียกว่ากฎของเวเบอร์ และเศษส่วนเวเบอร์ -10 dB หมายความว่า เราเริ่มสามารถตรวจจับความแตกต่างระหว่างความเข้มของ noise สองตัวได้เมื่อความเข้มของพวกมันต่างกัน 10% นอกจากนี้ยังมีการทดลองเพื่อดูเศษส่วนเวเบอร์ของ pure tone ความถี่ 1 kHz พบว่า เศษส่วนเวเบอร์ลดต่ำลงเมื่อระดับเสียงเพิ่มมากขึ้น สำหรับระดับสูงสุดถึง 100 dB SPL (ดูเส้นวงกลมดำ รูปบน) แต่เมื่อระดับสูงกว่า 100 dB SPL เศษส่วนเวเบอร์จะกลับเพิ่มขึ้นมาอีกครั้ง (ไม่ได้แสดงในรูป) กระนั้นความสามารถในการแยกยังอยู่ในเกณฑ์ดีที่ระดับเสียงสูงมากนี้ ตัวอย่างในงานศึกษาของ Viemeister กับ Bacon พบว่าเศษส่วนเวเบอร์เท่ากับ -6 dB SPL สำหรับ pure tone ระดับ 120 dB SPL ตรงนี้แหละครับที่เป็นต้นตอปัญหาที่น่าสนใจ มนุษย์สามารถแยกความเข้มเสียงที่ระดับสูงถึง 120 dB SPL ได้ ทั้ง ๆ ที่เส้นใยประสาทส่วนใหญ่ (ชนิด spontaneous rate สูง, ดู บทที่ 4) จะอิ่มตัวที่ 60 dB SPL หมายความว่า ถึงแม้คุณจะเพิ่มระดับเสียงกระตุ้นมากขึ้น แต่ firing rate ก็เท่าเดิม นั่นเท่ากับนิวรอนส่วนใหญ่ไม่อาจใช้ firing rate เพียงอย่างเดียวในการนำเสนอหรือบอกข้อมูลเกี่ยวกับระดับเสียงที่มีระดับสูงกว่า 60 dB SPL ได้ นอกจากนี้นะครับ พวกเส้นใยส่วนน้อยที่ spontaneous rate ต่ำ ถึงแม้พวกมันจะมีช่วงตอบสนองที่กว้างกว่า แต่ฟังก์ชั่น rate-level ของมันก็มีความชันน้อยเมื่อเทียบกับเส้นใยชนิด spontaneous rate สูง นั่นคือ การเปลี่ยนระดับในเส้นใยส่วนน้อยเหล่านี้ จะส่งผลกระทบต่อ firing rate ไม่มาก ฉะนั้น พวกมันจึงไม่น่าจะอ่อนไหวสักเท่าไรต่อความแตกต่างในความเข้ม ทำให้เกิดคำถามสำคัญว่า แล้วคนเราสามารถแยกความแตกต่างความเข้มที่ระดับเสียงสูงมากอย่าง 120 dB SPL ได้อย่างไร? คำอธิบายหนึ่งว่าเหตุใดเศษส่วนเวเบอร์ถึงได้มีค่าน้อย ๆ ที่ระดับ pure tone สูง ๆ คือ ผู้ฟังยังมี information เกี่ยวกับ excitation pattern ทั้งหมด ซึ่งข้อมูลตัวนี้แหละครับที่อาจช่วยให้เราสามารถแยกความเข้มเสียงที่ระดับเสียงสูงได้ มีเหตุผลสนับสนุนที่เป็นไปได้ 2 ข้อ (1) ถึงแม้ว่าเส้นใยประสาทส่วนใหญ่ที่มีความถี่ลักษณะเฉพาะใกล้กับความถี่ของ pure tone จะอิ่มตัวที่ระดับเสียงสูง แต่นิวรอนซึ่งมีความถี่ลักษณะเฉพาะอยู่ห่างจากความถี่ของ pure tone (หรือบริเวณบน basilar membrane ที่อยู่ไกลจากบริเวณที่มีการสั่นสูงสุด) ได้รับการกระตุ้นไม่มาก นิวรอนพวกนี้จึงยังไม่อิ่มตัว และสามารถใช้ firing rate ของพวกมันบอกการเปลี่ยนระดับเสียงได้ รูปนี้แสดงการจำลองกิจกรรมของเส้นใยชนิด sr (spontaneous rate) สูงและต่ำในโดเมนความถี่ลักษณะเฉพาะที่ตอบสนองต่อ pure tone ความถี่ 1 kHz ณ ระดับเสียงต่าง ๆ กัน กราฟนี้คือรูปแบบการกระตุ้น (neural excitation pattern) นะครับ เห็นว่า จุดสูงสุดของ excitation pattern จะอิ่มตัวสำหรับเส้นใย sr สูงที่ระดับเสียงสูง เพราะนิวรอนที่มีความถี่ลักษณะเฉพาะใกล้กับ 1 kHz ตามรูปนี้อิ่มตัว แต่นิวรอนที่มีความถี่ลักษณะเฉพาะอยู่ห่างออกมาจาก 1 kHz พอสมควรจะยังไม่อิ่มตัว เส้นใยของนิวรอนเหล่านี้จึงใช้บอกการเปลี่ยนแปลงระดับเสียงได้ (2) ผู้ฟังอาจรวบรวม information ทั่วทั้ง excitation pattern เพื่อเพิ่มประสิทธิภาพความสามารถในการแยกความเข้ม ยิ่งมีการใช้นิวรอนมากตัวก็ยิ่งมีความแม่นยำในการแทนความเข้มเสียง โดยเฉพาะ information จากฝั่งความถี่สูงของ excitation pattern อาจเป็นประโยชน์มาก เพราะฝั่งนี้จะแปรตามระดับของตัวกระตุ้นอย่างรวดเร็วเมื่อเทียบกับ excitation pattern ย่านความถี่กลาง ๆ มีนักวิจัยได้ทดสอบสมมติฐานที่ว่า information จากขอบ ๆ (skirts) ของ excitation pattern ถูกใช้ในการตรวจจับความแตกต่างของความเข้ม พวกเขาทดลองโดยการ masking บริเวณ skirts เหล่านี้ด้วย noise รูปด้านล่างแสดงผลลัพธ์จากการทดลองแยกความเข้มของ pure tone 1 kHz กรณีมี noise และไม่มี noise ซึ่ง noise ทำหน้าที่พราง information จากขอบข้าง ๆ ของ excitation pattern (เป็น noise ชนิด band-stop ที่มีความถี่ cutoff เท่ากับ 500 Hz และ 2 kHz) แต่กระนั้น การเพิ่ม noise ก็ทำให้ประสิทธิภาพลดลงไม่มาก แค่ทำให้กฎของเวเบอร์กลับมาเหมือนในกรณี wideband noise เท่านั้นแหละครับ ราวกับระบบรับรู้เสียงสามารถนำเสนอเสียงระดับสูง ๆ โดยใช้นิวรอนในช่วงความถี่ลักษณะแคบ ๆ เท่านั้น และส่วนใหญ่ นิวรอนเหล่านี้ก็อิ่มตัวเสียด้วย! ในบางสถานการณ์ ความเข้มสามารถแทนหรือนำเสนอได้ด้วยการล็อกเฟส (phase locking) ในนิวรอน จากความรู้บทที่ 4 เส้นใยประสาทจะส่งสัญญาณไฟฟ้าหรือถูกกระตุ้นที่เฟสเฉพาะเฟสใดเฟสหนึ่งของโครงสร้างละเอียดของ waveform เสียง ตัวอย่างเช่น ระบบรับรู้เสียงของเราอาจแยก pure tone ที่มาพร้อมกับ noise ได้จากการตรวจจับรูปแบบที่มีระเบียบ (regularity) จากรูปแบบไร้ระเบียบของ firing (เพราะ noise ทำให้เกิดรูปแบบไร้ระเบียบของ phase locking) นอกจากนี้ การเพิ่มความเข้มของ pure tone ในขณะที่มี noise อาจเท่ากับเพิ่มความเป็นระเบียบให้มากขึ้น ถึงแม้ว่าเส้นใยประสาทจะอิ่มตัวและไม่สามารถเปลี่ยนแปลง firing rate ได้ นั่นคือ รูปแบบของกิจกรรมในนิวรอนสามารถเปลี่ยนแปลงได้ตามระดับเสียง นี่อาจช่วยในการนำเสนอหรือแทนเสียงซึ่งซับซ้อนที่ระดับเสียงสูง ๆ ในกรณีตัวอย่างการทดลองเมื่อตะกี้ เส้นใยประสาทอาจแสดงการเปลี่ยนระดับเสียงด้วยการเปลี่ยนดีกรีของ synchronization ของ spike ของ pure tone และผลจากการเพิ่ม band-stop noise โดยหวังป้องกันการใช้ข้อมูลจาก skirts ของ excitation pattern อาจช่วยเพิ่ม dynamic range ของเส้นใยโดยไม่ได้ตั้งใจ แต่กระนั้น ความสามารถแยกความเข้มเสียงใน band-stop noise ก็ยังเป็นไปได้ที่เสียงระดับสูง ๆ และความถี่สูง ๆ ซึ่งสูงกว่าความถี่ที่คิดกันว่าจะไม่เกิด phase locking แล้ว นั่นหมายความว่า ถึงแม้ phase locking จะมีส่วนช่วยต่อการแยกความเข้มเสียงในบางสถานการณ์ แต่มันต้องมีอย่างอื่นอีก (ที่เรายังไม่รู้?, หนังสือค้างไว้แค่นี้) (การเปลี่ยนรูปแบบของ firing rate เป็นหัวข้อศึกษาที่กำลังทำในปัจจุบัน) Comparisons across Frequency and across Time แน่นอนว่าความดังของเสียงสัมพันธ์กับความเข้มสัมบูรณ์ (absolute intensity) ของเสียง กล่าวคือ ระดับความดันเสียงสูง ความดังก็ยิ่งมาก แต่ความเข้มสัมบูรณ์ก็เป็นตัววัดที่มีประโยชน์แค่ในบางสถานการณ์เท่านั้นแหละครับ เช่น ตอนเราจะประมาณความใกล้ไกลของแหล่งกำเนิดเสียงที่เราคุ้นเคย แต่ในบางสถานการณ์ เช่น การแยกแยะเสียงนั้น ความเข้มสัมบูรณ์ไม่ค่อยมีประโยชน์เท่าไร เพราะความเป็นสระ /i/ ก็ยังเหมือนเดิมไม่ว่าจะพูดที่ 50 dB หรือ 100 dB SPL นั่นคือ สิ่งสำคัญในการแยกแยะเสียงคือความเข้มสัมพัทธ์ (relative intensity) ของ features ในเสียง การเปรียบเทียบความเข้มสัมพัทธ์ทำได้ใน 2 โดเมน คือ เปรียบเทียบในโดเมนความถี่และในโดเมนเวลา การเปรียบเทียบความเข้มของสเปกตรัมแต่ละตัว (เปรียบเทียบในโดเมนความถี่) บางครั้งมีชื่อเรียกว่า profile analysis และมีการทดลองสำคัญอันหนึ่งในยุคต้น ๆ คือการทดลองของ Green และคณะ (1988) เขาให้ผู้ฟังฟังเสียง 2 เสียง ซึ่งแต่ละเสียงมีหลายความถี่ ในเสียงหนึ่งแต่ละความถี่จะมีความเข้มเท่ากันหมด ส่วนในอีกเสียงหนึ่ง จะมี tone ตัวหนึ่งที่มีความเข้มโดดออกมา สูงกว่าชาวบ้าน ดังรูปด้านล่าง การทดลองให้ผู้ฟังฟังหลายรอบ แต่ละรอบระดับเสียงโดยรวมก็เปลี่ยนไปอย่างสุ่ม และก็สุ่มให้เสียงที่มีโทนโดดอาจเป็นเสียงแรกหรือเสียงหลังก็ได้ 50-50 หน้าที่ของผู้ฟังคือ ให้ระบุว่าเสียงไหนเป็นเสียงที่มีโทนโดด Green พบว่า ผู้ฟังสามารถแยกได้ นั่นหมายถึง เราสามารถเปรียบเทียบความเข้มสัมพัทธ์ของสเปกตรัมได้ ซึ่งผลการทดลองก็ไม่น่าแปลกใจเท่าไรใช่มั้ยครับ เพราะถ้าเราทำอย่างนั้นไม่ได้ เราก็ไม่สามารถตรวจจับ formant ในเสียงสระได้ (formant คือ จุดยอดของสเปกตรัมเสียงพูด) เราก็ฟังเสียงพูดกันไม่รู้เรื่อง นอกจากนี้ยังพบว่า ความสามารถดังกล่าวแทบไม่ขึ้นอยู่กับช่วงระยะห่างระหว่างเสียง 2 เสียง (อย่างน้อยก็ห่างกันได้ถึง 8 วินาที) ไม่เหมือนกับความสามารถในการแยกความเข้มของ pure tone สองตัว ถ้าช่วงเวลาระหว่าง pure tone ทั้งสองยิ่งห่าง เราก็ยิ่งแยกไม่ได้ เช่นเดียวกับการเปรียบเทียบความเข้มในโดเมนความถี่ เราสามารถเปรียบเทียบความเข้มในโดเมนเวลาได้ด้วย (อันนี้ก็ไม่แปลกอีก เพราะการทดลองในหัวข้อก่อนหน้านี้ที่เกี่ยวกับ ΔI, ΔL ล้วนใช้ความสามารถเปรียบเทียบความเข้มในโดเมนเวลา) อันที่จริงสัญญาณเสียงที่ไม่เปลี่ยนแปลงตามเวลาแทบจะไม่มีข้อมูลอะไรให้คนคนฟังเลย ผู้เขียนแทรกอารมณ์ขันในหนังสือตอนนี้ว่า ถ้าแกพูด "eeee" ยาวไปเรื่อย ๆ เราก็คงไม่ได้ข้อมูลอะไรจากแก นอกจากข้อมูลเกี่ยวกับสภาพจิตของแก การเปรียบเทียบความเข้มในโดเมนเวลาทำให้เราสามารถรู้การเปลี่ยนแปลงของสเปกตรัม ในบทที่ 11 จะกล่าวถึงความสำคัญอย่างยิ่งยวดของเรื่องนี้ต่อการรับรู้เสียงพูด และก็แน่นอนว่าการเปรียบเทียบความเข้มในช่วงเวลาสั้น ๆ จะมีความแม่นยำมากกว่า, make sense!   Create Date : 11 พฤษภาคม 2556     Last Update : 23 สิงหาคม 2556 15:01:29 น. Counter : 3926 Pageviews.   0 comment Share Tweet

Frequency Selectivity [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 5 ในชื่อเดียวกัน หนังสือ The Sense of Hearing โดย Christopher J. Plack รายละเอียดบทที่ 2 - 4 ดูได้จากสารบัญกลุ่มเรื่องที่กำลังศึกษาตามลิงค์ด้านบนครับ ลำดับเนื้อหาตั้งแต่บทนี้เป็นต้นไปจะเรียงตามลำดับในหนังสือ ทำนองเดียวกับบทที่ 4 frequency selectivity คือ ความสามารถที่หูของเราแยกองค์ประกอบทางความถี่ที่แตกต่างกันของเสียงได้ ถ้าเปรียบเทียบกับการมองเห็นนะครับ ระบบการมองเห็นจะเป็นเหมือน place-to-place mapping คือ map หรือจับคู่แสงจากจุดต่าง ๆ ใน space กับตำแหน่งบนเรตินา ส่วนในระบบการรับรู้เสียง สิ่งแรกที่ทำคือ แยกองค์ประกอบความถี่ต่าง ๆ ของเสียงที่เข้ามาบน basilar membrane จึงเป็น frequency-to-place mapping นอกจากนี้ frequency selectivity ยังทำให้เราสามารถแยกเสียงที่เกิดขึ้นพร้อมกันได้ เช่น เราแยกได้ว่านี่เป็นเสียง double bass นี่เป็นเสียง piccolo ตอนที่สองเสียงนี้ถูกเล่นพร้อมกัน Frequency Selectivity on the Basilar Membrane การทดลองของ von Békésy ที่ผมได้เล่าสรุปในตอนที่แล้วนั้น เป็นการดูพฤติกรรมของ cochlea โดยการผ่าตัดศพ และ von Békésy ต้องใช้ระดับเสียงสูงถึง 140 dB SPL ในการกระตุ้น แต่จากการศึกษาปัจจุบัน เช่น จากการผ่าตัดหนู chinchilla และสัตว์ทดลองที่ถูกวางยาสลบ พบว่า cochlea ทำงานดีกว่าที่เคยรู้จากการศึกษาของ von Békésy มาก ทั้งในแง่ bandwidth ของฟิลเตอร์ และการแพร่ของ traveling wave (ซึ่งก็ไม่เห็นจะน่าแปลกใจตรงไหนเลยใช่มั้ยครับ) นั่นเท่ากับพูดว่า ความสามารถในการจูนเสียงของ cochlea ขึ้นอยู่กับ physiological state ของสัตว์ ในการทดลองสมัยใหม่ โดยทั่วไปจะผ่าเปิด cochlea เพื่อสังเกต basilar membrane บริเวณใกล้ ๆ base และตรวจวัดการเคลื่อนที่ของ membrane จากการสะท้อนของแสงเลเซอร์ที่ตกกระทบพื้นผิวของลูกแก้วเล็ก ๆ ที่วางบน membrane เทคนิคนี้ใช้ดูผลตอบสนองของตำแหน่งบน basilar membrane เพียงตำแหน่งเดียว ไม่ได้ติดตามดูทั้ง traveling wave รูปซ้ายมือแสดงกราฟ iso-level ที่แต่ละเส้นบ่งบอกถึงอัตราเร็วของตำแหน่งตำแหน่งหนึ่งบน basilar membrane (และเป็นตำแหน่งที่มีความถี่ลักษณะเฉพาะ หรือ characteristic frequency เท่ากับ 10 kHz) ในโดเมนความถี่ของ pure tone ที่ระดับเสียงต่าง ๆ กัน ตั้งแต่ 20 dB SPL ถึง 90 dB SPL อัตราเร็วของ basilar membrane ในกราฟนี้เขียนในหน่วย dB เทียบกับ 1 ไมโครเมตร/วินาที หมายความว่า ถ้า basilar membrane มีอัตราเร็ว 1 μm/s มันจะถูกแทนด้วยอัตราเร็ว 0 dB ในสเกลนี้ กราฟที่เห็นมาจากการทดลองในหนู chinchilla จากรูป จะเห็นว่า ยิ่งความถี่ของ pure tone เข้าใกล้ความถี่ที่มีการตอบสนองดีที่สุดของ basilar membrane ณ ตำแหน่งนั้น (เรียกว่า best frequency, ข้อควรระวัง อย่าเข้าใจว่า best freq. กับ characteristic freq. เป็นตัวเดียวกันนะครับ ค่ามันอาจจะเท่ากันก็ได้ นิยามของ characteristic frequency หรือ ความถี่ลักษณะเฉพาะคือ best frequency ที่ระดับความดันเสียงต่ำ) อัตราเร็วที่ตำแหน่งดังกล่าวก็จะยิ่งเพิ่มมากขึ้น พอความถี่ของ pure tone ออกห่างจาก best frequency การตอบสนองก็จะยิ่งน้อยลง แต่ละตำแหน่งบน basilar membrane ทำตัวเหมือน band-pass filter ที่ลดทอนองค์ประกอบความถี่ซึ่งอยู่ห่างจาก best frequency นอกจากนี้ รูปยังบอกแก่เราว่า ที่ระดับเสียงต่ำ ๆ นั้น basilar membrane แยกองค์ประกอบทางความถี่ที่แตกต่างกันได้ดีกว่าที่ระดับเสียงสูง ๆ เราจะเห็นว่าที่ระดับเสียงสูง ความกว้างของกราฟ iso-level จะกว้างขึ้น นั่นหมายความว่า แต่ละตำแหน่งจะตอบสนองต่อองค์ประกอบความถี่ในช่วงย่านที่กว้าง และ pure tone ตัวเดียว จะกระตุ้นตำแหน่งหลาย ๆ ตำแหน่งเป็นบริเวณกว้างบน basilar membrane ทำให้ traveling wave ครอบคลุมพื้นที่กว้างด้วย รูปขวายังบอก best frequency ของตำแหน่งใด ๆ บน membrane จะมีค่าลดลง เมื่อระดับเสียงเพิ่มมากขึ้น รูปนี้ ระดับเสียงเพิ่มจาก 20 dB ไปจนถึง 90 dB SPL, best frequency ลดจาก 10 kHz ลงไปเหลือ 7 kHz ด้วยเหตุนี้ โดยทั่วไปแล้วคำว่าความถี่ลักษณะเฉพาะจะใช้อ้างถึง best frequency ในการตอบสนองที่ระดับเสียงต่ำ ผลสืบเนื่องจากการลด best frequency เมื่อระดับเสียงเพิ่มขึ้นคือ ทำให้จุดสูงสุดของ traveling wave เลื่อนไปยัง base ของ cochlea เราเรียกปรากฏการณ์ดังกล่าวว่า basalward shift (การเลื่อนไปทาง base) ของ traveling wave ยังมีอีกวิธีที่สามารถใช้วัด frequency selectivity ของตำแหน่งใด ๆ บน basilar membrane นั่นคือ เปิดเสียงที่ความถี่แต่ละค่าเข้าหู แล้วหาระดับเสียงที่ทำให้ basilar membrane สั่น ตอนที่ความถี่ของ tone เข้าใกล้ best frequency ของตำแหน่งที่เราสนใจวัดอยู่นั้น ระดับเสียงจะต้องต่ำ ยิ่งเข้าใกล้ ยิ่งต่ำ เมื่อเราพล็อตกราฟความสัมพันธ์ระหว่างระดับเสียงที่ทำให้ basilar membrane สั่นกับความถี่ เราจะได้ tuning curve ดังรูปบนขวา สังเกต ที่ระดับเสียงต่ำ เส้นกราฟฝั่งความถี่สูงของ tuning curve จะดูลึกและชัน tuning curve อาจถือว่าเป็นรูปพลิกตั้งของกราฟฟิลเตอร์ สำหรับรูปด้านล่างแสดง iso-level กับ tuning curve ที่วัดใกล้ ๆ apex (แต่เป็นการวัดที่ tectorial membrane นะครับ) ณ ตำแหน่งที่มีความถี่ลักษณะเฉพาะ 500 Hz คงเห็นได้ไม่ยากว่า bandwidth ของฟิลเตอร์ในหน่วย Hz ที่ apex จะแคบกว่าที่ base จากความรู้เกี่ยวกับการตอบสนองต่ออิมพัลซ์ของฟิลเตอร์ ฟิลเตอร์ที่มี bandwidth แคบจะสั่นนานกว่า ฟิลเตอร์ที่มี bandwidth กว้าง หมายความว่า ถ้าหูได้ยินเสียงคลิกหนึ่งทีสั้น ๆ ตำแหน่งตรงที่อยู่ใกล้ apex ซึ่งมี bandwidth แคบจะสั่นนานกว่า (หลายสิบมิลลิวินาที) ขณะที่ตำแหน่งใกล้ base ซึ่งมี bandwidth กว้างกว่าจะสั่นแป๊ปเดียว ดังรูป รูปแสดงการสั่นของ 3 ตำแหน่งบน basilar membrane ตัวเลขความถี่ที่ระบุขวามือคือความถี่ลักษณะเฉพาะของแต่ละตำแหน่ง คาบการสั่นของ membrane เท่ากับคาบของ pure tone ที่ความถี่ลักษณะเฉพาะนั้น เมื่อย้อนกลับไปมองรูปแรกอีกที เราจะเห็นสมบัติความไม่เป็นเชิงเส้น (non-linearity) ที่ base ของ basilar membrane อย่างเด่นชัด เพราะในระบบเชิงเส้นนั้น แอมปลิจูดของ output จะต้องเป็นค่าคงที่เท่าของ input ไม่ว่า input จะมีระดับเท่าไรก็ตาม รูปด้านล่างแสดงอัตราเร็วของ basilar membrane ที่เปลี่ยนไปตามระดับของ input ณ จุดที่มีความถี่ลักษณะเฉพาะ 10 kHz ในระบบเชิงเส้น กราฟแสดงความสัมพันธ์ระหว่าง output กับ input บนสเกล dB จะต้องเป็นเส้นตรงที่มีความชันเท่ากับ 1 (ดูบทที่ 3) แต่จากรูป เราจะเห็นว่า การตอบสนองของ basilar membrane ค่อนข้างเป็นเชิงเส้นเฉพาะกรณีที่ความถี่ของสัญญาณกระตุ้นต่ำกว่าความถี่ลักษณะเฉพาะ (CF) แต่ที่ความถี่สูงกว่านั้น ความชันของกราฟจะลดลง อันเป็นลักษณะของระบบที่มีการบีบอัด (compressive system) กล่าวคือ ระดับของ input เพิ่มขึ้น 10 dB อาจทำให้ output เพิ่มขึ้นแค่ 2 dB การบีบอัดนี้มีความสำคัญนะครับ เพราะมันทำให้เราสามารถใช้ acoustic information ได้ในช่วงระดับเสียงที่กว้าง และก็เช่นเดียวกับสมบัติ frequency selectivity สมบัติความไม่เป็นเชิงเส้นของ basilar membrane ขึ้นอยู่กับสถานะทางกายภาพของสัตว์ รูปด้านล่างแสดงกราฟเปรียบเทียบกรณีสัตว์เป็นกับสัตว์ตาย เห็นว่า หลังจากตายแล้ว ความเป็นเชิงเส้นเพิ่มขึ้น และการตอบสนองก็ยากขึ้น การวัดโดยตรงส่วนใหญ่ทำที่ base ใกล้หน้าต่างวงรี เพราะผ่าตัดง่าย แต่กระนั้น การทดลองที่ทำทางฝั่ง apex ก็มีนะครับ และพบว่า basilar membrane มีการตอบสนองแบบเชิงเส้นมากกว่าที่ base ถึงแม้จะมีลักษณะบีบอัดเหมือนกัน แต่มากสุดก็แค่ 2:1 นอกจากนี้ การบีบอัดแถว ๆ apex ไม่ได้มีผลกระทบแค่กับความถี่ใกล้ ๆ ความถี่ลักษณะเฉพาะของตำแหน่งนั้น (ดังเช่นบริเวณ base) แต่ส่งผลกับความถี่ input ในย่านกว้าง ความไม่เป็นเชิงเส้นของ cochlea ยังก่อให้เกิดผลสืบเนื่องสำคัญอีก 2 ประการ (1) suppression หรือ การข่มทับ หมายถึง เหตุการณ์ที่ basilar membrane ลดการตอบสนองต่อองค์ประกอบความถี่ตัวหนึ่งเมื่อมีองค์ประกอบความถี่อีกตัวหนึ่งโผล่เข้ามา ตัวอย่างเช่น ผมเล่น pure tone 1 kHz 40 dB SPL การตอบสนองของตำแหน่งบน basilar membrane ต่อ tone นี้อาจลดลงถ้าผมเล่น pure tone 1.3 kHz 60 dB SPL เพิ่มเข้าไปอีกตัว อันนี้เห็นชัดเจนว่าเป็นพฤติกรรมที่ไม่เป็นเชิงเส้น (2) distortion หรือ ความผิดเพี้ยน ทั้งนี้เพราะระบบที่ไม่เป็นเชิงเส้นจะผลิตองค์ประกอบความถี่ที่ไม่มีใน input ออกมาให้ที่ output ในหูปกติสมบูรณ์นั้น จะมีความไม่เป็นเชิงเส้นสูงและทำให้เกิด distortion มาก โดยเฉพาะอย่างยิ่ง inter-modulation distortion ซึ่งเกิดขึ้นเมื่อองค์ประกอบตั้งแต่สองตัวขึ้นไปมีปฏิสัมพันธ์กันที่ตำแหน่งใดตำแหน่งหนึ่งบน basilar membrane แน่นอน องค์ประกอบเหล่านี้จะต้องอยู่ไม่ห่างกันเพื่อให้พวกมันตกอยู่ในช่วงความถี่ที่จะถูกบีบอัดโดยตำแหน่งเดียวบน membrane เมื่อเกิดความผิดเพี้ยนแบบนี้ขึ้น เราจะพูดว่ามีการสร้าง combination tone ขึ้นมา โดย combination tone ตัวนี้นะครับจะแพร่กระจายหรือเดินทางจากจุดที่มันถูกสร้าง ไปกระตุ้นตำแหน่งบน basilar membrane ที่มีความถี่สอดรับ (หรือเป็นความถี่ลักษณะเฉพาะ) ของ combination tone และในบางครั้ง เราก็ได้ยินเสียงนี้ชัดเจนเสียด้วย ทั้ง suppression และ distortion เป็นสมบัติของหูที่มีสุขภาพดี และสมบัติดังกล่าวจะสูญหายไปถ้า cochlea เสื่อมหรือถูกทำร้ายทำลาย ฟังดูเป็นเรื่องตลกนะครับ หูดี ๆ ทำให้เกิดการผิดเพี้ยนมากกว่าหูที่ไม่ดี นั่นคือ หูที่มีสภาพไม่ดี (= การตอบสนองของ basilar membrane เป็นเชิงเส้น และ tuning curve แผ่กว้าง) จะให้ผลการคัดแยกความถี่คล้ายกับหูดี ๆ ที่ระดับความดันเสียงมีค่าสูง ๆ โดยเฉพาะในแง่ที่ว่า tuning curve ของทั้งสองกรณีกว้างเหมือนกัน สำหรับหูที่มีสุขภาพดีนั้น tuning curve ที่ระดับเสียงต่ำถึงกลางจะมีลักษณะลึกแคบเป็นตัว V และการตอบสนองต่อ tone ที่ความถี่ใกล้ความถี่ลักษณะเฉพาะเกือบเป็นเชิงเส้นที่ระดับเสียงต่ำ (โน้ต: คำว่าระดับเสียงสูงหรือระดับเสียงต่ำ ไม่ได้เกี่ยวกับเสียงสูง-เสียงต่ำนะครับ แต่หมายถึง ระดับเสียง หรือ sound level ที่มีค่าสูงหรือค่าต่ำ ความดันมากหรือความดันน้อย อันที่จริงบริบทมันทำให้คิดถึงเสียงสูง-เสียงต่ำไม่ได้อยู่แล้วล่ะ แต่อยากย้ำกันมึน) แต่จะมีการบีบอัดอย่างมากที่ระดับเสียงสูง นอกจากนี้ ในการจูนของตำแหน่งบน basilar membrane ที่อยู่ใกล้ ๆ base จะมี best frequency (หรือ ความถี่เรโซแนนต์) สูงกว่าที่ระดับเสียงต่ำเมื่อเทียบกับที่ระดับเสียงสูง เราพูดจะว่าการตอบสนองของหูที่มีสุขภาพไม่ดีนั้น เป็นการตอบสนองแบบ passive ของ basilar membrane ดังที่เคยวัดได้โดย von Békésy (เพราะ von Békésy ผ่าตัด cochlea จากศพในการทำการทดลอง) ลักษณะดังกล่าวเป็นผลมาจากสมบัติเชิงกลพื้นฐานของ cochlea โดยเฉพาะอย่างยิ่งสมบัติความแข็งทื่อที่แตกต่างกันตลอดทั้งสาย membrane จึงทำให้เหมือนกับมี "อะไรบางอย่าง" เพิ่มเข้ามาในหูที่สุขภาพดีที่รับผิดชอบต่อ หรือส่งผลกระทบต่อ การเคลื่อนไหวของ basilar membrane ที่ base และ "อะไรบางอย่าง" นั้นจะต้องทำหน้าที่เหมือนตัวขยายที่ขึ้นอยู่กับระดับและความถี่ (level- and frequency-dependent amplification) ของการตอบสนองของ basilar membrane เสียงระดับต่ำจะถูกขยาย ในขณะที่เสียงระดับสูงไม่ถูกขยาย และการขยายหรือ gain นี้ จะเกิดขึ้นกับความถี่ที่ใกล้ความถี่ลักษณะเฉพาะของแต่ละตำแหน่งบน basilar membrane ทีนี้ ความถี่ลักษณะเฉพาะตรงบริเวณ base ของ cochlea จะสูงกว่า best frequency ทำให้จุดหักมุมของ tuning curve เลื่อนไปทางความถี่ต่ำกว่า สมมติ คุณมีฟิลเตอร์ที่มี bandwidth กว้างอยู่ตัวหนึ่ง และอยากทำให้ bandwidth แคบลง เพราะคุณต้องการเอาเฉพาะความถี่ที่ใกล้เคียงกับความถี่ศูนย์กลางของฟิลเตอร์ จะทำยังไงครับ? คำตอบ โดยทั่วไปมี 2 วิธี (1) เพิ่มการลดทอนขององค์ประกอบความถี่ที่อยู่ห่างจากความถี่ศูนย์กลาง หรือ (2) ขยายองค์ประกอบความถี่ที่อยู่ใกล้ความถี่กลาง และวิธีที่ 2 นี่แหละที่ cochlea เลือกใช้ แต่กระนั้น ความถี่ที่ได้รับการขยายจะสูงกว่าความถี่กลางของฟิลเตอร์ตัวเดิม (คำว่า ตัวเดิม ในที่นี้คือ passive basilar membrane) และเนื่องจากไม่มีการขยายที่ระดับเสียงสูง ความถี่กลางของฟิลเตอร์จะปรับลงลงมาเท่ากับกรณี passive จากรูป เส้นล่างเป็นกรณี passive (อาจจะเป็นกรณีหูสุขภาพไม่ดี หรือหูสุขภาพดีแต่ถูกกระตุ้นที่ระดับเสียงสูงก็ได้) เส้นบนคือกรณี active (หูที่มีสุขภาพดีและกระตุ้นที่ระดับเสียงต่ำ) รูปซ้ายแสดงให้เห็นการขยายการเคลื่อนที่ของ basilar membrane ที่ความถี่ที่สูงกว่าความถี่กลางของหูแบบ passive สำหรับรูปขวาแสดงให้เห็นว่า ค่า gain จะสูงกว่าที่ระดับความดันของ input ต่ำกว่า พูดอีกอย่างว่า gain ค่อย ๆ ลดลงเมื่อระดับ input เพิ่มขึ้น เราเชื่อว่า outer hair cell เป็นตัวการสำคัญในกระบวนการขยายนี้ ทฤษฎีปัจจุบันบอกว่า outer hair cell ตอบสนองต่อการสั่นของ basilar membrane โดยการยืดหรือหดด้วยอัตราเดียวกับความถี่ของเสียงกระตุ้น เฉกเช่นการผลักชิงช้าถูกจังหวะเวลา การยืดหดนี้อาจช่วยให้ basilar membrane สั่นมากขึ้นเมื่อได้รับการกระตุ้นจาก tone ที่มีความถี่ใกล้ความถี่ลักษณะเฉพาะ ค่า gain สูงสุดอาจสูงถึง 50 dB แต่ก็ไม่ใช่ทุกระดับ input (เพราะมันไม่เป็นเชิงเส้น) เป็นไปได้ว่า outer hair cell อาจไม่สามารถตอบสนองได้เพียงพอที่ระดับเสียงสูง จึงทำให้ gain ลด และได้ผลลัพธ์เป็นการตอบสนองแบบบีบอัดต่อ tone ที่ความถี่ลักษณะเฉพาะ และทำให้ tuning curve กว้าง จากผลงานตีพิมพ์ปี 2000 ของ Zheng และคณะ เราสามารถระบุตัวการรับผิดชอบต่อการเปลี่ยนแปลงความยาวของ outer hair cell ได้แล้วนะครับ นั่นคือ โปรตีนชื่อ prestin ในเยื้อหุ้มเซลล์ของ outer hair cell ซึ่งโปรตีนตัวนี้จะเปลี่ยนรูปร่างของมันตามการเปลี่ยนแปลงศักดาไฟฟ้าของเซลล์ (ดูบทที่ 4) รูปร่างของ prestin ที่เปลี่ยน จะทำให้ความยาวของ outer hair cell เปลี่ยน และอาจทำให้การเคลื่อนที่ของ basilar membrane เปลี่ยน ทำให้เกิดการขยาย outer hair cell บอบบางต่อการบาดเจ็บทางกายภาพมากครับ การทดลองเรื่องนี้ในสัตว์จึงต้องใช้ความระมัดระวังอย่างยิ่งยวด เพื่อไม่ให้มันถูกทำลาย และอยู่ในสภาพที่ดี เพื่อการตอบสนองของ cochlea ที่ถูกต้อง ยาอ่อน ๆ อย่างแอสไพรินก็มีฤทธิ์ยับยั้งการทำงานของ outer hair cell ชั่วคราวได้ นอกจากนี้ ถ้าเจอกับเสียงดังมาก ๆ มันก็ถูกทำลายได้ง่าย พังแล้วพังเลย ไม่มีทดแทน คนเราพอแก่ตัว การทำงานของ outer hair cell ก็ค่อย ๆ เสื่อมไป เชื่อกันว่า การทำงานผิดปกติของ outer hair cell นี่แหละที่ทำให้หูตึง สูญเสียความสามารถในการได้ยิน นอกจากนี้ outer hair cell ยังสามารถถูกควบคุมโดยใยประสาทจากสมองได้ด้วย ประเด็นสุดท้ายก่อนขึ้นหัวข้อใหม่คือ otoacoustic emission คำว่า oto- แปลว่า หู, otoacoustic emission หมายถึง การให้กำเนิดเสียงจากหู อันนี้เป็นการค้นพบปลายช่วงทศวรรษ 1970 โดย Kemp ว่าหูคนเรานี่นะครับ สามารถปล่อยเสียงได้ด้วย ตอนแรกก็ไม่มีใครเชื่อ แต่เดี๋ยวนี้ได้รับการยืนยันอย่างดี แถมยังนำมาใช้ประโยชน์ในการตรวจสอบเบื้องต้นว่าหูเด็กทารกมีปัญหาผิดปกติอะไรรึเปล่า เพราะการสร้างเสียงโดยหูเป็นลักษณะข้อหนึ่งของหูที่มีสุขภาพดี ถ้าเราเล่นเสียงอิมพัลซ์หรือเสียงคลิกป้อนเข้าหู หูอาจจะสร้างเสียงที่มีองค์ประกอบความถี่บางค่ากลับออกมาให้ แบบนี้เรียก cochlear echoes และการสร้างเสียงดังกล่าวเกิดจากกระบวนการใน cochlea ทีนี้ ถ้ามี pure tone มากกว่าหนึ่งตัวเป็น input เสียงที่หูสร้างอาจประกอบด้วย distortion ของ combination tone การสร้างเสียงแบบนี้เรียกว่า distortion product otoacoustic emission แถมพลังงานที่ปล่อยออกมาอาจมากกว่าพลังงานของเสียงกระตุ้นได้ด้วย ซึ่งนี่ก็เป็นหลักฐานสนับสนุนการทำงานด้านขยาย (amplification) ชั้นดี ยังมีบางครั้งที่หูสร้าง pure tone ขึ้นมาเองโดยไม่ต้องมี input เรียกว่า spontaneous otoacoustic emission และนี่อาจเป็นผลจากการทำงานของ outer hair cell ที่ตำแหน่งใดตำแหน่งหนึ่งบน basilar membrane และก็เป็นไปได้เช่นกันครับที่ spontaneous emission จะดังพอให้คนอื่นได้ยิน Neural Frequency Selectivity นักวิทยาศาสตร์สามารถยัดไมโครอิเล็กโทรดเข้าไปในเส้นประสาทของสัตว์ทดลองหรือหนู chinchilla เพื่อดูกิจกรรมที่เกิดขึ้นภายในเส้นใยใด ๆ ได้นะครับ และพบว่า เส้นใยแต่ละเส้นจะมีสมบัติการจูนความถี่แทบจะเหมือนกับสมบัติการจูนของตำแหน่งบน basilar membrane ที่มันยึดติดอยู่ นั่นคือ เส้นใยจะตอบสนองต่อ pure tone ที่ความถี่ลักษณะเฉพาะด้วย firing rate สูง และ firing rate จะต่ำลง เมื่อความถี่ของ pure tone เลื่อนออกห่างจากความถี่ลักษณะเฉพาะ รูปนี้แสดง frequency threshold tuning curve กราฟสร้างจากการหาระดับของ pure tone ในโดเมนความถี่ ที่ทำให้ firing rate ของนิวรอนเพิ่มขึ้นในระดับที่เริ่มวัดได้ ซึ่งกราฟจะสมมูลกับ tuning curve ของ basilar membrane จากรูปเป็น tuning curve ของนิวรอน 5 ตัว จากเส้นประสาทรับรู้เสียงของหนู chinchilla ทางซ้าย เราพล็อตความถี่แบบเชิงเส้น จะเห็นว่า bandwidth กว้างขึ้นเมื่อ ความถี่ลักษณะเฉพาะมากขึ้น ส่วนทางขวาพล็อตบนสเกล logarithm จะเห็นว่า bandwidth เมื่อเทียบกับความถี่ลักษณะเฉพาะ จะแคบลงเมื่อความถี่ลักษณะเฉพาะเพิ่มขึ้น จากบทที่ผ่านมา เราได้พูดถึงการตอบสนองต่อ pure tone ที่ความถี่ลักษณะเฉพาะของเส้นใยประสาทกลุ่มที่มี spontaneous rate สูงว่า ฟังก์ชั่น rate-level ของมันจะชันกว่า และอิ่มตัวที่ระดับเสียงต่ำกว่ากลุ่มที่มี spontaneous rate (sr) ต่ำ (ดูหัวข้อ Activity in the Auditory Nerve ในบทที่ 4) ข้อแตกต่างสำคัญระหว่างใยประสาทสองกลุ่มนี้คือ กลุ่ม sr สูงจะมีความอ่อนไหว (sensitive) มากกว่ากลุ่ม sr ต่ำอย่างมาก ดังนั้นพวกมันจึงตอบสนองต่อการเคลื่อนไหวของ basilar membrane ที่ระดับที่ฟังก์ชั่นการตอบสนองของ basilar membrane เป็นเชิงเส้น (นั่นคือ ส่วนระดับเสียงต่ำที่ชันของฟังก์ชั่น, หากดูรูป rate-level function บทที่ 4 ส่วนดังกล่าวคือส่วนชัน ๆ ทางซ้ายมือในช่วงประมาณ 25 - 40 dB SPL) ณ บริเวณระดับเสียงต่ำนี้ การสั่นของ basilar membrane จะเพิ่มขึ้นอย่างรวดเร็วเมื่อระดับของ input เพิ่ม ทำให้ firing rate ในเส้นใยประสาทเพิ่มขึ้นอย่างรวดเร็วตามระดับ input ด้วย ด้วยเหตุนี้แหละครับ firing rate ที่นิวรอนอิ่มตัวถึงได้อยู่ที่ระดับต่ำ เส้นใยกลุ่ม sr ต่ำมีความอ่อนไหวน้อยกว่า ทำให้ช่วงกว้างของระดับที่มันอ่อนไหวนั้นตกอยู่ในบริเวณที่มีการบีบอัดของฟังก์ชั่นตอบสนองของ basilar membrane ฉะนั้น การเปลี่ยนแปลงระดับ input จึงก่อให้เกิดการเปลี่ยนแปลงน้อยนิดที่ระดับ output ทำให้ firing rate ในเส้นใยประสาทเปลี่ยนไปแค่นิดเดียว ฟังก์ชั่น rate-level ของมันจึงดูแบน ๆ ตื้น ๆ และไปอิ่มตัวเอาที่ระดับ input สูง ๆ รูปนี้แสดง firing rate ในใยประสาทรับรู้เสียงกลุ่ม sr ต่ำของสัตว์ทดลองที่ความถี่ลักษณะเฉพาะ 20 kHz เมื่อเสียงกระตุ้นคือ pure tone ที่ความถี่ 20 kHz และ 17 kHz เห็นว่าที่ 20 kHz ความชันของฟังก์ชั่น rate-level ต่ำกว่าเมื่อเทียบกับที่ความถี่กระตุ้นต่ำกว่าความถี่ลักษณะเฉพาะ ทั้งนี้เพราะ ฟังก์ชั่น rate-level ของมันขึ้นอยู่กับสมบัติความไม่เป็นเชิงเส้นของ cochlea นั่นคือ ฟังก์ชั่นนี้จะต้องตอบสนองต่อ tone ที่ความถี่ต่ำกว่าความถี่ลักษณะเฉพาะอย่างค่อนข้างเป็นเชิงเส้นมากกว่า อันที่จริง จากการตั้งสมมติฐานว่า การตอบสนองต่อ tone ที่ความถี่ต่ำกว่าความถี่ลักษณะเฉพาะเป็นการตอบสนองแบบเชิงเส้นนี่แหละครับ ที่ทำให้ Yates, Winter กับ Robertson (1990) สามารถใช้ฟังก์ชั่น rate-level ของใยประสาทที่ตอบสนองต่อ tone ที่ความถี่ต่ำกว่าหรือเท่ากับความถี่ลักษณะเฉพาะ ในการย้อนกลับไปสร้างการตอบสนองของ basilar membrane ต่อ tone ที่ความถี่ลักษณะเฉพาะได้ ประเด็นคือ rate-level function สะท้อนถึง ฟังก์ชั่นตอบสนองของ basilar membrane เราได้พูดถึง suppression อันเป็นผลสืบเนื่องจาก non-linearity ใน cochlea จากหัวข้อที่แล้ว ก่อนจบหัวข้อนี้ เราจะพูดถึงการดูหรือการวัด suppression จากการตอบสนองของเส้นประสาทรับรู้เสียง ทำได้โดย วัด firing rate ของใยประสาทเส้นหนึ่งที่ตอบสนองต่อ pure tone ระดับเสียงต่ำที่ความถี่ลักษณะเฉพาะของใยเส้นนั้น ต่อมา เพิ่ม pure tone เข้าไปอีกตัว ถ้า pure tone ตัวที่สองตกอยู่ภายใน tuning curve ของเส้นใยประสาท มันก็จะทำให้ firing rate เพิ่มขึ้น แต่มีบางค่าระดับและบางความถี่ของ pure tone ตัวที่สองที่อยู่นอก tuning curve ที่จะทำให้ firing rate ในเส้นใยที่เรากำลังวัดลดลง ดังรูป รูปนี้แสดง two-tone suppression ในเส้นประสาท เส้นสีดำเข้มคือ tuning curve ของเส้นใยประสาทที่ความถี่ลักษณะเฉพาะ 8 kHz จุดสามเหลี่ยมคือ pure tone อันแรก เมื่อไรก็ตามที่มี pure tone ตัวที่สองอยู่ในพื้นที่แรเงา การมีอยู่ของตัวที่สองนี้จะทำให้ firing rate ของเส้นใยที่ cf = 8 kHz ลดลงอย่างน้อย 20% Psychophysical Measurements ที่ผ่านมา เราได้เรียนรู้ความสามารถแยกองค์ประกอบความถี่ของ basilar membrane คำถามคือ อะไรเป็นผลสืบเนื่องจาก frequency selectivity ในแง่ของการรับรู้ (perception) คำตอบหนึ่งคือ มันทำให้เราสามารถได้ยินองค์ประกอบความถี่หนึ่งแบบแยกออกมาจากองค์ประกอบความถี่อื่นเมื่อองค์ประกอบเหล่านั้นผสมอยู่รวมกันได้ สมมติว่าผมเปิด noise ที่มีช่วงความถี่ 1 kHz - 1.2 kHz ให้คุณฟัง ต่อมา ผมเพิ่ม tone ความถี่ 2 kHz ที่ระดับต่ำกว่าระดับของ noise ถึง 20 dB กรณีนี้ คุณได้ยิน tone สบาย ๆ เพราะมันแยกจาก noise บน basilar membrane พวกมันเป็นเสียงสองเสียงที่กระตุ้น basilar membrane กันคนละที่ แต่ถ้าผมเปลี่ยนเป็น tone 1.1 kHz คุณจะไม่ได้ยินเสียงมันเลย เราพูดว่า tone ถูก mask โดย noise เพราะว่า noise ได้พรางไม่ให้เรารับรู้การมีอยู่ของ tone การพราง (masking) แบบนี้จะเกิดขึ้นเมื่อไรก็ตามที่กิจกรรมบน basilar membrane เนื่องจากเสียงเสียงหนึ่ง (เป็น masker) อำพรางหรือทำให้เราไม่รับรู้กิจกรรมของเสียงอีกเสียงหนึ่ง (เป็น signal) ที่เราพยายามจะฟัง ถ้า masker และ signal มีความถี่ห่างกัน masker จะต้องมีความดันสูงกว่า signal มากหากคิดจะพรางมันให้ได้ แต่ถ้า masker กับ signal มีความถี่ใกล้ ๆ กัน masker ก็ต้องการความดันมากกว่า signal แค่ไม่กี่ dB ที่ผ่านมา เราวัด frequency selectivity โดยใช้เทคนิคทางสรีระหรือทางกายภาพในการศึกษาในสัตว์อื่นที่ไม่ใช่คน สำหรับคน เราใช้เทคนิคทาง psychophysical อย่าง masking ในการวัด frequency selectivity ได้ครับ ตัวอย่าง เราป้อน pure tone ที่ระดับค่อนข้างต่ำ เช่น 10 dB เหนือขีดเริ่มการได้ยิน (เราเรียกระดับนี้ว่า 10-dB sensation level) ต่อมา ป้อน noise ย่านความถี่แคบหรือ pure-tone masker ที่ความถี่ค่าหนึ่ง แล้วค่อย ๆ เพิ่มระดับเสียงของ masker ขึ้นกระทั่งผู้ฟังไม่สามารถได้ยิน pure tone ตัวแรก ทำซ้ำเช่นนี้โดยเปลี่ยนความถี่ของ masker ไปเรื่อย ๆ แล้วพล็อตกราฟระดับความดันที่เริ่มเกิด masking ในโดเมนความถี่ของ masker จะได้ psychophysical tuning curve psychophysical tuning curve จะแสดงรูปร่างของ band-pass filter ที่มีความถี่กลางเท่ากับความถี่ของสัญญาณ pure-tone ตัวแรก เราจะเห็นว่าหน้าตามันก็เหมือน ๆ กับ basilar membrane tuning curve และ neural tuning curve รูปข้างบนนี้เป็นการทดลองที่ lab ของผู้เขียนเองนะครับ psychophysical tuning curve ที่ 4 kHz โดยให้ masker เกิดก่อน signal ตามช่วงเวลาที่เห็น จาก 20 ms ถึง 100 ms อันนี้เรียกว่า forward masking (รายละเอียดจะพูดในบทที่ 8) เห็นว่าถ้าช่วง gap ระหว่าง masker กับ signal ยิ่งนาน ระดับเสียงของ masker ก็ต้องยิ่งมากตามไปด้วย สังเกตว่า เมื่อระดับเพิ่มขึ้น tuning curve จะกว้างขึ้น (= สมบัติ frequency selectivity ลดลง) และจุดหักมุมของ tuning curve (จุดนี้คือจุดที่เป็น best frequency) จะเลื่อนลดความถี่ลง ทำนองเดียวกับ basilar membrane tuning curve ผู้เขียนเล่าว่าเทคนิคที่ได้อธิบายไปนั้นเป็นเพียงหนึ่งในหลาย ๆ เทคนิค และผลลัพธ์ที่ได้จากทุกเทคนิคก็สอดคล้องกันทั้งหมด ในส่วนต่อมา ผู้เขียนอธิบายเทคนิคของ Patterson (1976) ซึ่งว่าเป็นเทคนิคที่ใช้ในการประมาณรูปร่างของฟิลเตอร์ที่ได้รับความนิยมสูงสุด เรียก notched-noise technique ในเทคนิคนี้ pure-tone signal จะมาคู่กับ noise สองตัว ตัวหนึ่งความถี่สูงสุดของมันต่ำกว่าความถี่ของ tone ส่วนอีกตัวหนึ่ง ความถี่ต่ำสุดของมันสูงกว่าความถี่ของ tone โดย noise สองตัวนี้จะทำหน้าที่เป็น masker นั่นคือ tone จะอยู่ระหว่างช่องว่าง (spectral notch) ของ noise ดังรูป พื้นที่แรเงาสีดำแปรผันตามพลังงานของ noise ที่ผ่านฟิลเตอร์ที่ความถี่กลางเท่ากับความถี่ของ signal ถ้าความกว้างของ spectral notch เพิ่ม noise ที่ผ่านก็จะลดลง และ signal ถูกตรวจจับได้ง่ายขึ้น โดยทั่วไป signal จะปรากฏพร้อม ๆ ในเวลาเดียวกับ noise นะครับ แต่มันก็อาจจะปรากฏหลังจาก noise ในกรณีที่เราต้องการสำรวจ forward masking ก็ได้เหมือนกัน ระดับต่ำสุดที่ตรวจจับได้ของ signal (เรียก signal threshold) ถูกกำหนดให้เป็นฟังก์ชั่นของช่องว่างสเปกตรัม (spectral gap) ระหว่าง signal กับขอบของ noise แต่ละตัว ถ้าแถบของ noise อยู่ใกล้กับ signal จะทำให้พลังงานของ noise ปริมาณมากผ่านฟิลเตอร์ที่มีความถี่กลางเท่ากับความถี่ของ signal และ signal threshold จะมีค่าสูง แต่ถ้า spectral notch เพิ่ม ค่า threshold ดังกล่าวจะลดลง ฉะนั้น เราสามารถประมาณรูปร่างหน้าตาของฟิลเตอร์ได้ด้วยการดู signal threshold ที่เปลี่ยนแปลงไป เมื่อ spectral notch เปลี่ยนแปลง ข้อดีของวิธีที่ให้ signal อยู่ระหว่าง noise สองตัวคือ คือ มันจำกัดความเป็นไปได้จากกรณีการฟังแบบ off-frequency ให้ลดต่ำลง (การฟังแบบ off-frequency คือ สถานการณ์ที่ผู้ฟังตรวจจับสัญญาณได้ด้วยฟิลเตอร์ที่จูนสูงหรือต่ำกว่าความถี่ของสัญญาณ) ข้อเสียของ off-frequency คือ มันอาจทำให้เราประมาณ sharpness ของการจูนมากเกินจริง จากการทดลอง masking ด้วยเทคนิค notched-noise ดังกล่าว ทำให้ Glasberg กับ Moore (1990) ได้ประมาณ ERB สำหรับฟิลเตอร์ (ในหน่วย Hz) ว่าเป็นไปตามสมการ           ERB = 24.7(0.00437 fc + 1) เมื่อ fc คือ ความถี่ศูนย์กลางของฟิลเตอร์ (ในหน่วย Hz) เมื่อมองตามสมการนี้ สำหรับความถี่ที่มากกว่า 1 kHz เราจะพบว่าโดยประมาณแล้ว ค่า ERB แปรผันตรงกับความถี่กลาง (เท่ากับพูดว่า Q เป็นค่าคงที่ เพราะ Q = fc/bandwidth) และมีค่าประมาณ 11% ของความถี่กลางที่ความถี่สูง ๆ สมการนี้ไม่เป็นจริงที่ระดับเสียงสูงนะครับ นอกจากนี้ หลักฐานใหม่ ๆ ยังบอกว่าฟิลเตอร์ที่ความถี่สูงและระดับเสียงต่ำอาจจะมีความคม (sharpness) กว่าที่เคยคิดกัน ยังมีจุดอ่อนอีกประการในสมการของ Glasberg กับ Moore เนื่องจากพวกเขาใช้ simultaneous masking (= masker กับ signal ปรากฏพร้อม ๆ กัน) ทำให้ผลจาก masking บางส่วนอาจเกิดจากการ suppression แต่ถ้าเราใช้ forward masking จะไม่เกิด suppression เพราะ masker กับ signal ไม่ได้ปรากฏพร้อมกันทางกายภาพบน basilar membrane กรณีเปลี่ยนไปใช้ forward masking เราจะได้ tuning curve ที่คมขึ้นที่ระดับเสียงต่ำ และ ERB อาจมีค่าเพียง 5% ของความถี่กลางที่ 8 kHz ประเด็นสุดท้ายที่ผู้เขียนพูดถึงในบทนี้คือ excitation pattern (รูปแบบการกระตุ้น) อย่าลืมว่าตอนนี้เรามอง cochlea เหมือนกับ bank ของ band-pass filter ที่มีย่านความถี่ผ่านซ้อนทับกัน, excitation pattern ก็คือการพล็อต output ของฟิลเตอร์แต่ละตัวในโดเมนของความถี่กลางของมัน รูปบนซ้ายแสดง สเปกตรัมของ pure tone ความถี่ 1 kHz 80 dB SPL รูปบนขวาแสดง excitation pattern ของ pure tone ตัวเดียวกันที่ระดับ 40 60 และ 80 dB SPL สังเกตว่าจุดสูงสุดของ excitation pattern ไม่ได้เพิ่มขึ้นมากนักตามระดับ input ที่เพิ่มขึ้นมาก ทั้งนี้เพราะ basilar membrane บีบอัดที่ความถี่ลักษณะเฉพาะเท่ากับความถี่ของ tone แต่ที่ความถี่ลักษณะเฉพาะสูงกว่าความถี่ tone การตอบสนองของ basilar membrane ค่อนข้างเป็นเชิงเส้น ส่วนรูปล่างแสดงกรณีสระ /i/ ("ee") สังเกตว่า ฮาร์มอนิกส์ไม่กี่ตัวแรกของสระเท่านั้นจะที่สร้างจุดยอดที่แยกเป็นลูก ๆ (bumps) ใน excitation pattern ทั้งนี้เพราะ ระยะห่างระหว่างฮาร์มอนิกเป็นค่าคงที่ แต่ฟิลเตอร์กว้างขึ้น ๆ เมื่อความถี่เพิ่มมากขึ้น ขณะที่ฟิลเตอร์ซึ่งมีความถี่กลางอยู่ระหว่างฮาร์มอนิกส์สองตัว จะมี output ต่ำกว่า เพราะฮาร์มอนิกส์จะถูกลดทอนโดยฟิลเตอร์ตัวนั้น ส่วนที่ความถี่สูง ฮาร์มอนิกส์หลาย ๆ ตัวตกอยู่ในฟิลเตอร์แต่ละตัว การเปลี่ยนแปลงของความถี่กลางจึงส่งผลกระทบน้อยนิดต่อระดับ excitation มันจึงดูเป็นลูกเดียวใหญ่ ๆ แทนที่จะเป็นหลายลูกเล็ก ๆ เหมือนกรณีความถี่ต่ำ นั่นคือ ระบบการรับรู้เสียงสามารถแยกฮาร์มอนิกส์ต่ำกว่าใน complex tone ได้ แต่ไม่สามารถแยกฮาร์มอนิกส์ที่สูงกว่าได้   Create Date : 09 พฤษภาคม 2556     Last Update : 23 สิงหาคม 2556 14:57:59 น. Counter : 3799 Pageviews.   0 comment Share Tweet

Audio Watermarking Based on Spread Spectrum Communication Technique [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 7 How could music contain hidden information? หนังสือ Applied Signal Processing: A MATLABTM-Based Proof of Concept (Springer, 2009) เขียนโดย C. Baras, N. Moreau กับ T. Dutoit เราสามารถมอง watermarking ในสัญญาณเสียงเป็นเรื่องของปัญหาการส่งลำดับบิต 1 กับ 0 ผ่านช่องทางสื่อสารที่มี noise เยอะมากเป็นพิเศษได้ครับ โดยการมองแบบนี้ บิตที่เราจะส่งก็คือ watermark bit และ noise คือ สัญญาณเสียงนั่นเอง ฉะนั้น การทำ watermarking ก็เทียบเท่ากับการออกแบบตัวรับและตัวส่งที่สอดคล้องกับช่องทางพิเศษ รูปด้านล่างแสดงการมอง watermarking เป็นปัญหา communication ปัญหาหนึ่ง สำหรับ watermarking เราต้องออกแบบ SNR ให้ต่ำมาก (SNR = Psignal/Pnoise) เพื่อให้หูคนไม่สามารถได้ยินข้อมูลที่จะฝังหรือซ่อน ผลสืบเนื่องจาก SNR ต่ำคือ bit rate ต่ำตาม (ดีที่สุดที่เป็นไปได้อยู่ที่หลักร้อยบิตต่อวินาที) และ error rate มีค่าสูง (ประมาณ 10-3 เมื่อเทียบกับระบบสื่อสารอย่าง ADSL ซึ่งอยู่ที่ 10-6) Spread Spectrum Signals เริ่มแรก การสื่อสารด้วยเทคนิค Spread spectrum (SS) ใช้ในงานทางด้านการทหาร เพราะข้อเด่นของมันคือ 1. วิธีนี้ทนทาน (robust) ต่อการรบกวนในช่วงความถี่แคบ ๆ, 2. เป็นการส่งแบบแอบ ๆ ซ่อน ๆ และ 3. ความปลอดภัยในการส่งข้อมูล สัญญาณ SS มีลักษณะเฉพาะอยู่ 2 ประการ 1. bandwidth ของสัญญาณ SS ถูกทำให้กว้างกว่า bandwidth ของข้อมูลเดิมอย่างมาก (ทั่วไปประมาณ 10-100 เท่าสำหรับงานด้านพาณิชย์ และประมาณ 1,000 - 106 เท่า สำหรับงานการทหาร) การที่พลังงานมันแผ่กระจาย (spread) ในย่านที่กว้างนั้น ทำให้ PSD ต่ำลง ทำให้สัญญาณ SS มีโอกาสไปตีกับสัญญาณย่านความถี่แคบน้อยลง การสื่อสารย่านความถี่แคบแทบทำอะไรระบบ SS ไม่ได้เลย เพราะว่าตัวรับของระบบจะรวบรวมสัญญาณตลอดย่านที่กว้างมาก ๆ ในการดึงข้อมูลออกมา ข้อดีอีกประการจาก PSD ต่ำคือ เราสามารถทำให้มันต่ำกว่า PSD ของ noise ได้ อันนี้แหละครับคือลักษณะเด่นในการส่งข้อมูลแบบแอบ ๆ ซ่อน ๆ ของมัน 2. มีการใช้ spreading sequence (บางทีก็เรียก spreading code หรือ pseudo-noise) ในการสร้างสัญญาณ SS ย่านความถี่กว้างจากข้อมูลที่จะส่ง ซึ่งโค้ด spreading sequence นี้จะต้องเป็นที่รู้กัน รู้ตรงกัน ทั้งฝั่งส่งและฝั่งรับ ลักษณะ 2 อย่างนี้เป็นข้อดีใช่มั้ยครับ คำถาม ต้องเสียอะไรเป็นการแลกเปลี่ยนมั้ย? คำตอบ spectral efficiency หรือประสิทธิภาพของสเปกตรัมลดลง ประสิทธิภาพของสเปกตรัมนิยามจากอัตราส่วนระหว่างบิตเรตต่อ bandwidth ซึ่งเทคนิค SS จะให้ค่าที่ต่ำกว่า 1/5 ขณะที่เทคนิคมาตรฐานอื่น ๆ ให้ค่าเกือบ 1 Direct Sequence SS (DSSS) ใน DSSS หรือ time hopping นั้น สัญญาณ DSSS จะสร้างจากการคูณแต่ละคาบเวลาของหนึ่งบิต (bit-sized period หรือ Tb) ของสัญญาณที่จะส่ง (ในที่นี้สัญญาณที่จะส่งคือ watermark) ด้วย pseudo-noise ที่ประกอบจากลำดับลำดับอย่างสุ่มของพัลซ์สี่เหลี่ยม ±1 ซึ่งมีคาบเท่ากับ Tc ดังรูป รูปขวา บนสุดคือสัญญาณที่จะส่ง (watermark) มี Tb = 0.2 วินาที รูปกลางคือ pseudo-noise มี Tc = Tb/16 และรูปล่างคือสัญญาณ SS ที่ได้จากการคูณแต่ละคาบ Tb ของรูปบนด้วยรูปกลาง สำหรับรูปซ้าย แสดง PSD ของสัญญาณที่จะส่ง (หรือ รูปขวาบน) กับ PSD ของสัญญาณ SS เมื่อ Tc = Tb/4 และ Tb/16 ตามลำดับ เห็นว่า Tc ยิ่งต่ำ PSD ยิ่งต่ำ และที่ Tc = Tb/16 ต่ำกว่า PSD ของ noise เราคำนวณ PSD ของสัญญาณ SS ได้ไม่ยาก หากถือว่าสัญญาณที่จะส่งนั้นเป็นรหัสไบนารี่สุ่มแบบ NRZ ที่ประกอบจากพัลซ์สี่เหลี่ยมคาบ Tb และแอมปลิจูด ± 1/Tb เราจะได้           PSDNRZ(f) = [sinc2(fTb)]/Tb และเนื่องจากสัญญาณ SS เองก็เป็นสัญญาณ NRZ ที่พัลซ์มีคาบเท่ากับ Tc และแอมปลิจูด ± 1/Tb เราได้           PSDSS(f) = [Tcsinc2(fTc)]/Tb2      (ดังพล็อตในรูปซ้าย) Communication Channel Design เริ่มจากตัวส่ง (Emitter) โดยระบบสื่อสารแสดงดังรูปด้านล่าง สัญญาณเสียง x(n) ในที่นี้คือ noise ของระบบ มีอัตราสุ่มตัวอย่างเท่ากับ Fs Hz ถูกนำไปรวมเข้ากับ v(n) หรือสัญญาณ SS ของ watermark ที่สร้างมาจากการคูณ (หรือมอดูเลต) ลำดับของ watermark (bm ∈ {0,1}) ที่มีความยาวของลำดับเท่ากับ M บิต กับ pseudo-noise (หรือ spreading sequence, c(n)) ที่ประกอบด้วยตัวอย่างจำนวน Nb ตัว และเขียนแทนด้วยเวกเตอร์ c = [c(0), c(1), ..., c(Nb - 1)]T เจ้าเวกเตอร์ c นี้เราอาจสังเคราะห์ขึ้นมาจากตัวสร้างลำดับสุ่มเทียมที่มีค่าใน {-1, +1} อาทิ Walsh-Hadamard sequence หรือ Gold sequence เราไม่เอา bm มาใช้โดยตรง เพราะ bm ∈ {0, 1} เราก็แปลงมันเป็นสัญลักษณ์ชุดใหม่เรียกว่า am = 2bm - 1 ∈ {-1, +1} แล้วใช้คูณกับ c ก็จะได้ vm           vm = amc หรือพูดว่า vm = +c ถ้า am = 1 (หรือ bm = 1) และ vm = -c ถ้า am = -1 (หรือ bm = 0) หลังจากนั้นจะเอา v(n) มาขยายด้วย gain g เพื่อควบคุม SNR ระหว่าง v(n) กับ x(n) จะเห็นว่า เราส่งข้อมูล (หรือฝังข้อมูล) 1 บิตทุก ๆ ตัวอย่าง Nb ตัว ดังนั้นบิตเรต R จึงคำนวณได้จาก Fs/Nb มาดูทางด้านฝั่งรับ (Receiver) บ้าง จากรูป เราได้ ym = gvm + xm หรือ ym = +gc + xm เมื่อ am = +1 และ ym = -gc + xm เมื่อ am = -1 โดย xm = [x(mNb, x(mNb+1), ..., x(mNb+Nb-1)]T เป็นเวกเตอร์ของตัวอย่างของ noise (หรือเสียง) ในช่องทางสื่อสาร และ m คือ frame index สำหรับบิตฝั่งรับหาได้จาก            (arg max = argument of the maximum, สัญลักษณ์ข้างบนหมายถึง ค่า b ที่ทำให้ P(b|ym) มีค่าสูงสุด) ในกรณีที่ช่องทางการสื่อสารเป็นช่องแบบ AWGN (additive white Gaussian noise) หรือช่องทางที่บวก white noise (หมายถึงสัญญาณสุ่มที่มี PSD คงที่) ซึ่งแอมปลิจูดของ noise มีการกระจายแบบปกติ (หรือ Gaussian distribution) ค่าดังกล่าวจะสมมูลกับการประมาณจากเครื่องหมายของผลคูณสเกล่า (αm) ระหว่าง ym กับ c            เพราะ เมื่อแทนที่ P(b|ym) ตามความสัมพันธ์ของเบส์ เราได้            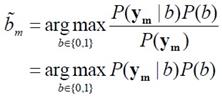โดยที่ P(ym) เป็น priori probability ของ ym ซึ่งไม่มีผลกระทบต่อการประมาณค่า bm และ P(b) คือ priori probability ของแต่ละค่าที่เป็นไปได้ของ b และในกรณีที่ความเป็นไปได้นี้เท่ากัน มันก็จะไม่มีผลต่อการประมาณ bm ด้วยเช่นกัน ฉะนั้น            ในกรณีช่องทางสื่อสารแบบ AWGN นั้น xm เป็น ตัวแปรสุ่ม Gaussian แบบ Nb-dimensional multivariate ที่มีค่าเฉลี่ยเท่ากับ 0 และเมตริกซ์ความแปรปรวนร่วม (covariance matrix) เท่ากับ σx2I เมื่อ I คือเมตริกซ์เอกลักษณ์ Nb มิติ ทีนี้ ym ก็เป็นตัวแปรสุ่ม Gaussian ที่มี Nb ตัวแปรด้วย เพราะ ym = gvm + xm โดยมีค่าเฉลี่ยเท่ากับ amgc และเมตริกซ์ความแปรปรวนร่วมเดียวกับ xm จึงได้            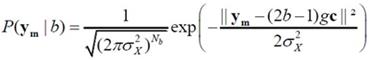หรือ            เนื่องจาก b ∈ {0, 1} นั่นทำให้ (2b - 1)2 = 1 ไม่ว่า b จะมีค่าเท่าไร บรรทัดสุดท้ายของสมการนี้จึงบอกว่า เราสามารถหา bm ได้จาก เครื่องหมายของผลคูณเชิงสเกล่า αm ระหว่าง ym กับ c            รูปต่อไปนี้แสดงภาพกรณีฝัง bm = 1 ลงในเวกเตอร์เสียง x ได้เวกเตอร์หลังจากฝังแล้ว y ซึ่งคำนวณจาก gv + x หรือ gc + x เพราะ bm = 1 และทางฝั่งรับจะตีความว่า "1" ถ้า α > 0 รูปซ้ายแสดงกรณี <x,c> เป็นบวก และไม่ว่า g จะเป็นค่าบวกเท่าไรก็ตาม ย่อมทำให้ α > 0 ฉะนั้น bm = 1 นั่นคือดึงหรือรับข้อมูลได้ตรงกับที่ฝังหรือส่ง สำหรับรูปขวา เป็นกรณีที่ bm = 0 เนื่องจาก <x,c> เป็นค่าลบ และ g น้อยเกินไป กรณีนี้ดึงหรือรับข้อมูลได้ผิดนะครับ ถ้าอยากให้รับได้ถูก ต้องหาทางทำให้ g > <x,c>/|c|2 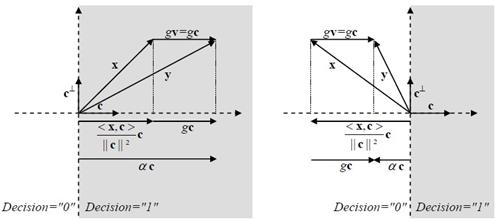Error Rate PDF ของ αm ที่ g = 1 และ σx2 = 20 dB แสดงดังรูป เมื่อค่า R เท่ากับ 50, 100 และ 120 ตามลำดับ (R = Fs/Nb โดยทั่วไป Fs เป็นค่าคงที่ 44.1 kHz ฉะนั้น อาจพูดว่า กราฟนี้พล็อตที่ความยาว Nb ต่าง ๆ กัน) รูปซ้ายคือกรณี b = 0 รูปขวา b = 1 αm เป็นตัวแปรสุ่ม Gaussian มิติเดียว ที่มีค่าเฉลี่ย (2bm - 1)g และความแปรปรวน σx2/|c|2            จะเห็นได้ว่า ความน่าจะเป็นที่ αm เป็นบวกเมื่อ bm = 0 และความน่าจะเป็นที่ αm เป็นลบเมื่อ bm = 1 ไม่เท่ากับศูนย์ (หมายความว่า มันมีโอกาสที่จะรับหรือดึงบิตออกมาได้ผิดค่า) และเมื่อค่า R มากขึ้น (กราฟ PDF เตี้ยลง และกระจายกว้างขึ้น) ความน่าจะเป็นดังกล่าวทั้ง 2 กรณีก็เพิ่มมากขึ้นตาม ความน่าจะเป็นที่จะอ่านค่าได้ผิดพลาดนี้หาได้จาก            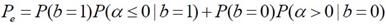ถ้าสัญลักษณ์แต่ละตัวมี priori probability เดียวกัน (นั่นคือ P(b=1) = P(b=0)) ความน่าจะเป็นของ error สามารถประมาณโดยใช้กราฟด้านบน มีค่าเท่ากับ พื้นที่ซ้อนทับกันของ P(αm|bm = 0) และ P(αm|bm = 1) ซึ่งเราจะคำนวณ Pe ได้   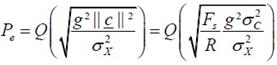         โดยที่ 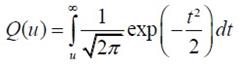ในสมการนี้เราใช้ σc2 = |c|2/Nb = กำลังของ pseudo-noise หรือ spreading sequence โดยประมาณ เห็นว่า ความน่าจะเป็นที่จะอ่านค่าผิดขึ้นอยู่กับ SNR ของ watermarking (= g2σc2/σx2) กับ R รูปด้านล่างแสดงกราฟ ซ้าย พล็อต Q(√u) กับ u ขวาพล็อต Pe(R) กับ R ที่ค่า SNR ต่าง ๆ กัน เมื่อ Fs = 44.1 kHz Informed Watermarking ในระบบสื่อสารทั่วไปเราไม่รู้ noise ของช่องทางสื่อสารล่วงหน้า จึงเอามามันมาใช้ประโยชน์ในการปรับ gain ตอนเข้ารหัสไม่ได้ แต่สำหรับ watermarking นั้น เป็นไปได้ครับ เพราะ noise ในที่นี้คือเสียงที่เราจะใช้ซ่อนข้อมูล เราจะเริ่มด้วยการดูวิธีตรงไปตรงมาอย่างการปรับ gain เพื่อให้ตรวจรับข้อมูลได้อย่างไม่มีข้อผิดพลาด นั่นคือ ทางฝั่งส่งหรือฝั่งเข้ารหัสจะต้องมีการปรับค่า g ซึ่งเป็นฟังก์ชั่นของเวลาเพื่อชดเชยความผันผวนของกำลังแบบทันทีทันใดในสัญญาณเสียง และรักษา SNR ให้คงที่ ซึ่งทำได้ง่าย ๆ โดยการประมาณค่า σx2 ของเฟรมเสียง (~ 20 ms) แล้วกำหนดค่า g ให้แปรตาม σx ถ้าย้อนกลับไปดูกราฟ PDF ของ α เห็นว่า เราทำให้ error หมดไปได้ด้วยการทำให้กราฟทั้ง 2 แยกออกห่างจากกัน และทำได้โดยการเพิ่มค่า g ถ้าเราปรับให้ค่า g ของแต่ละเฟรมสอดคล้องกับ            ผลที่ได้คือไม่มี error ทางฝั่งรับข้อมูล (ต่อจากนี้ ค่า g จะเปลี่ยนไปในแต่ละเฟรม เราจะเขียนแทน g ของแต่ละเฟรมด้วย gm) วิธีกำหนดค่า g อาจทำโดย ถ้า βm มีเครื่องหมายเดียวกับ am ค่า gm เป็นค่าบวกเท่าไรก็ได้ แต่ถ้า βm มีเครื่องหมายตรงกันข้ามกับ am ก็กำหนดให้ค่า gm = -βm/am อย่างไรก็ตาม ในทางปฏิบัติ ช่องทางสื่อสารก็จะเพิ่ม noise เข้ามาอีกอยู่ดี ฉะนั้น เวกเตอร์ที่ฝั่งรับได้รับจึงไม่ใช่ ym แต่เป็น ym+pm ทำให้            จึงต้องมีการเพิ่มระยะ Δg เข้าไปด้วย (Δg กำหนดจากความแปรปรวนโดยประมาณของสัญญาณรบกวนของช่องทางสื่อสาร) เพื่อความมั่นใจและปลอดภัยว่าระบบยังคงเป็น error-free ฉะนั้น gm จะต้องผ่านเงื่อนไข            รูปด้านล่างแสดง inform watermarking ของเวกเตอร์เสียง x ที่ถูกฝังด้วย "1" ได้ผลลัพธ์เป็นเวกเตอร์ y = gv + x = gc + x ซึ่งเราต้องเลือกค่า g เพื่อทำให้ y ตกอยู่ในพื้นที่แรเงาสีเทาขวามือ (ถ้าไม่ตกในพื้นที่นี้ ตัวรับจะไม่อ่านได้ค่า "1") รูปแสดงรายละเอียด 2 กรณี กรณีแรก x(1) เราเลือกค่า g ที่ไม่ติดลบอะไรก็ได้ เช่น 0 เวกเตอร์ y ก็ตกอยู่ในพื้นที่สีเทา สำหรับกรณีที่สอง x(2) เราต้องเลือกเค่า g สูง ๆ และเพื่อรองรับ noise อื่น ๆ ในช่องทางสื่อสาร ระยะห่าง 2Δg ถูกนำมาใช้เป็นช่องว่างระหว่างการตัดสินใจ "1" หรือ "0" ของฝั่งรับ แน่นอนครับ ปัญหาที่เกิดจากการทำให้ error-free ด้วยวิธีนี้คือ คุณภาพเสียงของ y จะต่ำและเสียงผิดเพี้ยนจากการเพิ่ม gv ที่ g มาก ๆ เข้ากับ x ทางออกต่อปัญหานี้คือใช้สมบัติรับรู้เสียงของมนุษย์เข้ามาช่วยทำให้เราไม่ได้ยินข้อมูล watermark วิธีการคือ เราใช้ Psychoacoustic Model (PAM) มาช่วยในการคำนวณ masking threshold (รายละเอียดของ PAM ผมจะเขียนถึงในบล็อกตอนอื่นนะครับ และเนื้อหาตามหนังสือบทนี้ ผู้เขียนถือว่าผู้อ่านรู้จัก PAM มาเป็นอย่างดีแล้ว) นั่นคือ ถ้า PSD ของ watermark Sw(f) อยู่ต่ำกว่า PSD ของ masking threshold Φ(f) มันจะทำให้เราไม่ได้ยิน watermark หรือพูดอีกอย่างหนึ่งว่า เสียงต้นฉบับไม่ถูกรบกวน และเนื่องจากประสิทธิภาพของระบบ watermarking เป็นฟังก์ชั่นของ SNR ฉะนั้น ประสิทธิภาพดีสุดที่เกิดขึ้นที่ Sw(f) = Φ(f) เราสามารถทำได้โดยเอาฟิลเตอร์ที่จะดัดแปลงองค์ประกอบความถี่ตามการรับรู้ G(f) หรือ perceptual shaping filter ไปแทนที่ gain g ดังรูป โดยความนิยมนั้น G(f) เป็น all-pole filter: ถ้า v(n) ของฟิลเตอร์มีลักษณะแบบเดียวกับ white noise (ค่าเฉลี่ยเท่ากับศูนย์และความแปรปรวนสม่ำเสมอ) การปรับสัมประสิทธิ์ของฟิลเตอร์เพื่อให้ output w(n) ของมันมี PSD Sw(f) นั้น เป็นปัญหาสังเคราะห์หรือปัญหาออกแบบฟิลเตอร์ทั่ว ๆ ไป (แก้ชุดของสมการเชิงเส้น Yule-Walker) ทางด้านฝั่งรับ ก็ต้องเพิ่ม G-1(f) ก่อน demodulator แต่ทีนี้มีปัญหาว่า ฝังรับไม่มี x(n) (เป็น watermarking ชนิด blind) ซึ่ง x(n) เป็นตัวที่เราใช้สร้าง G(f) ฉะนั้น G-1(f) จึงต้องสร้างขึ้นมาแบบประมาณ ๆ จาก y(n) โดยความแม่นยำของตัว G-1(f) แบบประมาณนี้ขึ้นอยู่กับ 1. robustness ของ PAM ต่อ watermark และ 2. noise อื่น ๆ ในช่องทางสื่อสาร หลังจากนั้น เราคำนวณ bm คล้ายเดิม แต่คราวนี้เราดูเครื่องหมายของ <zm,c> แทน เมื่อ z(n) คือ output ของ G-1(f) ถ้าเราถือว่าหรือสมมติว่า G-1(f) ที่อยู่ ณ ฝั่งรับนั้นสามารถถูกสร้างให้เป็นอินเวิร์สของ G(f) ได้จริง ๆ เราจะได้ zm = vm + rm เมื่อ r(n) คือ x(n) หลังจากผ่าน G-1(f) การใช้ G-1(f) (มีชื่อเรียก zero-forcing equalizer) จะส่งผลให้ SNR ที่ output ของมันมีค่าต่ำมาก กล่าวคือ กำลังงานของสัญญาณ v(n) มีค่าน้อย ๆ เมื่อเทียบกับกำลังงานของสัญญาณเสียงที่ผ่าน equalizer หรือ r(n) เนื่องจาก PSD ของ v(n) กับ r(n) แตกต่างกัน ดังนั้น จึงเป็นไปได้ที่จะฟิลเตอร์ z(n) ในแบบที่ผลลัพธ์จากการฟิลเตอร์เพิ่มค่า SNR ซึ่งทำได้โดยการขยายองค์ประกอบสเปกตรัมของ z(n) ที่อยู่ภายใต้ v(n) และลดทอนองค์ประกอบสเปกตรัมของ z(n) ที่อยู่ภายใต้ r(n) หน้าที่ดังกล่าวเป็นของ FIR Wiener filter H(z) ดังรูปข้างบนที่เราเอาไปต่อท้าย G-1(f) ในส่วนของการออกแบบฟิลเตอร์ผมจะเขียนถึงอีกทีในบล็อกตอนอื่น อันที่จริง เนื้อหาในบทนี้ หลังจากผู้เขียนแนะนำ Wiener filter แสดงสมการ transfer function กับ ชุดสมการ Wiener-Hopf แล้วก็จบในภาคทฤษฎีเลยครับ   Create Date : 05 พฤษภาคม 2556     Last Update : 6 พฤษภาคม 2556 16:26:38 น. Counter : 3534 Pageviews.   0 comment Share Tweet

A Journey Through the Auditory System [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 4 ในชื่อเดียวกัน หนังสือ The Sense of Hearing โดย Christopher J. Plack จะเริ่มกล่าวจากหัวข้อ 4.2 The Cochlea ละหัวข้อแรก 4.1 From Air to Ear ซึ่งได้พูดถึงไปก่อนหน้านี้ในบล็อกหลาย ๆ ตอนแล้ว สำหรับเนื้อหาสรุปของบทที่ 2 และ 3 ดู The Nature of Sound (สรุป) กับ Production, Propagation, and Processing of Sound (สรุป) อนึ่ง ลำดับเนื้อหาที่จะสรุปในตอนนี้ ผมไม่เรียงเป็นข้อตามส่วน Summary เหมือน 2 บทแรก แต่เรียงตามลำดับหัวข้อของหนังสือ The Cochlea ที่ cochlea ของหูชั้นในนี่แหละครับที่การสั่นของคลื่นเสียงถูกแปลงเป็นสัญญาณไฟฟ้า (electrical neural activity) cochlea เป็นท่อขนาดเล็กมีของเหลวอยู่ภายใน ยาวประมาณ 3.5 เซ็นติเมตร เส้นผ่านศูนย์กลางเฉลี่ย 2 มิลลิเมตร อันที่จริง เส้นผ่านศูนย์กลางจะค่อย ๆ เล็กลงตามระยะห่างจากหน้าต่างวงรีหรือบริเวณที่เรียกว่า base โดยเส้นผ่านศูนย์กลางเล็กสุดที่ apex ท่อนี้ขดเป็นก้นหอยประมาณ 2.5 รอบ ผนังแข็งนะครับคล้ายกระดูก ฉะนั้น เราจะจับ cochlea ที่ขดเป็นก้นหอยออกมาคลี่เป็นเส้นตรงไม่ได้ รูปด้านล่างแสดงภาพตัดขวางของ cochlea เห็นว่าท่อตามแนวยาวถูกแบ่งโดย membrane สองอัน ได้แก่ Reissner's membrane กับ basilar membrane ทำให้เกิดห้องหรือช่องว่างหรือท่อย่อยซึ่งเต็มไปด้วยของเหลว 3 ส่วน มีชื่อเรียก scala vestibuli, scala media กับ scala tympani ซึ่ง s. vestibuli กับ s. tympani เชื่อมต่อกันผ่านช่องเปิดเล็ก ๆ เรียก helicotrema ระหว่าง basilar membrane กับผนังของ cochlea ที่ apex (ดูรูป) ส่วน media เป็นท่อย่อยที่แยกออกไปต่างหาก มีส่วนประกอบของเหลว (endolymph) แตกต่างจากอีกสองท่อย่อย (perilymph) รูปต่อมาเป็นภาพตัดขวางขยายโครงสร้างที่เป็นเจลาตินบน basilar membrane เรียกว่า tectorial membrane ซึ่งมี organ of Corti อยู่ระหว่าง membrane ทั้งสอง organ of Corti ประกอบด้วย hair cells หลายแถว (hair cells เป็นเซลล์ชนิดพิเศษชนิดหนึ่ง พวกมันจะมีส่วนคล้ายขนเล็ก ๆ เรียกว่า stereocilia ยื่นออกมา) และเซลล์สนับสนุนแบบต่าง ๆ รวมถึงปลายประสาท (nerve endings) ใน cochlea ของคน จะมี hair cells หนึ่งแถวที่อยู่ด้านใน เรียกว่า inner hair cells และด้านนอกมีได้มากถึง 5 แถว เรียก outer hair cells ตลอดความยาว cochlea คาดว่ามี hair cells ภายในราว 3,500 เซลล์ และภายนอกราว 12,000 เซลล์ และ ปลายสุดของ stereocilia ของ outer hair cells จะทิ่มฝังอยู่ใน tectorial membrane (ขณะที่ hair ของ inner ไม่ฝังนะครับ) หน้าที่ของ outer hair cells คือ เปลี่ยนสมบัติเชิงกลของ basilar membrane (รายละเอียดจะพูดถึงในบล็อกตอนอื่น) ส่วนหน้าที่ของ inner hair cells คือ แปลงการสั่นของ basilar membrane ไปเป็นสัญญาณไฟฟ้า The Basilar Membrane เสียงเข้ามายัง cochlea ผ่านทางหน้าต่างวงรี (มันคือ membrane อันหนึ่งที่ปิดกั้นระหว่างหูชั้นกลางกับ cochlea) ของเหลวใน cochlea แทบไม่สามารถบีบอัดได้ ดังนั้นเมื่อหน้าต่างวงรีถูกผลักเข้ามาใน cochlea เนื่องจากการสั่นของกระดูกโกลน ทั้ง Reissner's membrane และ basilar membrane จะถูกผลักลง และหน้าต่างวงกลมซึ่งอยู่อีกด้านหนึ่งของ base จะถูกผลักออก นั่นคือ การสั่นของกระดูกโกลนทำให้ basilar membrane สั่น basilar membrane เป็นส่วนสำคัญต่อการรับรู้เสียงในสัตว์เลี้ยงลูกด้วยนม มันทำหน้าที่แยกองค์ประกอบทางความถี่ของเสียง บริเวณ base ใกล้กับหน้าต่างวงรีนั้น basilar membrane แคบและแข็งทื่อ บริเวณดังกล่าวนี้อ่อนไหวต่อความถี่สูง ส่วนที่ปลายอีกด้านหนึ่ง บริเวณ apex จะกว้างกว่าและไม่แข็งทื่อเท่า จึงเป็นบริเวณที่อ่อนไหวต่อความถี่ต่ำ (ดูรูปข้างบน จะเห็นว่า basilar membrane กว้างขึ้นเมื่อ cochlea มีขนาดเล็กลง) สมบัติอันนี้ของ membrane เปลี่ยนแปลงอย่างต่อเนื่องจาก base ถึง apex ดังนั้น แต่ละตำแหน่งบน basilar membrane จะอ่อนไหวต่อความถี่เฉพาะบางค่า (เราเรียก characteristic frequency) ตัวอย่างเปรียบเทียบเพื่อให้เข้าใจกลไกการทำงานของ basilar membrane ให้นึกถึงสปริงแขวนเป็นแถวยาวเรียงกันหลายอันบนท่อนไม้ที่วางในแนวขนานกับพื้นโลก โดยสปริงแต่ละอันผูกติดอยู่กับมวลก้อนหนึ่ง สปริงที่อยู่ซ้ายมือสุดแข็งทื่อสุด (stiff) (ตอนเรียน ม.ปลาย stiffness ของสปริงเราจะแสดงด้วยค่าคงที่สปริงหรือค่านิจสปริง k ซึ่งความถี่ของการเคลื่อนที่แบบซิมเปิ้ลฮาร์มอนิกของมวลติดสปริงยกกำลังสองจะแปรตาม k และแปรผกผันกับมวล) และความแข็งทื่อของสปริงแต่ละอันที่แขวนอยู่นั้น ค่อย ๆ ลดลงเรื่อย ๆ เมื่อสปริงแขวนใกล้ปลายทางด้านขวามากขึ้น ๆ นั่นคือ สปริงขวามือสุด เป็นสปริงที่หลวมหรือคลายที่สุด อันนี้เรากำลังเปรียบเทียบให้ระบบสปริงติดมวลบนท่อนไม้เป็น basilar membrane โดยซ้ายมือคือ base และขวาคือ apex สมมติว่าเรามีสปริงอันหนึ่ง แล้วผูกปลายด้านหนึ่งของสปริงติดกับมวล แล้วปล่อยให้มันเคลื่อนที่ขึ้นลงเด้งดึ๋ง ๆ เองสักพักตามธรรมชาติก่อนหยุดนิ่ง อัตราการสั่นของมวลนั่นแหละครับคือความถี่เรโซแนนต์ของระบบ ถ้าสปริงแข็งทื่อมาก มวลก็จะเด้งดึ๋งด้วยความเร็วสูง นั่นคือ ความถี่มาก แต่ถ้าสปริงคลาย (loose) มวลก็จะเคลื่อนที่ขึ้นลงช้า มีความถี่ต่ำ ทีนี้ ถ้าคุณใช้มือจับปลายอีกข้างหนึ่งของสปริง แล้วเคลื่อนมือขึ้นลงด้วยความถี่สูงกว่าความถี่เรโซแนนต์ของระบบ มวลก็จะสั่นไม่มาก แต่ถ้ามือของคุณเคลื่อนที่ขึ้นลงด้วยความถี่เรโซแนนต์ การสั่นก็จะมาก กลับมาที่แท่งไม้ซึ่งมีสปริงติดมวลผูกเรียงเป็นแนวยาว ถ้าเราจับแท่งไม้นั้น ถือในแนวขนานกับพื้นโลก แล้วเคลื่อนแท่งไม้ขึ้นลงด้วยความถี่ค่าหนึ่ง สิ่งที่เราจะเห็นคือ มีมวลกลุ่มหนึ่งสั่นมากกว่ามวลที่เหลือ ทั้งนี้เป็นเพราะ ความถี่ของการเคลื่อนแท่งไม้ขึ้นลงใกล้เคียงกับความถี่เรโซแนนต์ของมวลกลุ่มนั้น ถ้าความถี่ของท่อนไม้มีค่าน้อย ๆ มวลที่สั้นแรงจะอยู่ทางขวา (apex) ของท่อนไม้ แต่ถ้าความถี่ของท่อนไม้มาก มวลจะอยู่ทางซ้าย (base) ทีนี้ ถ้าคุณสามารถเคลื่อนแท่งไม้ขึ้นลงในรูปแบบที่มีความถี่สองค่ารวมกัน (ทำได้นะครับ นึกภาพมือจับแท่งไม้สั่น ๆ ด้วยความถี่สูง ขณะเดียวกันแขนก็ยกมือสั่น ๆ นั้นขึ้นลงด้วยความถี่ต่ำ) การสั่นของมวลทางด้านซ้ายจะเป็นเพราะความถี่สูง ส่วนการสั่นของมวลทางขวาจะเป็นเพราะความถี่ต่ำ นั่นเสมือนกับระบบนี้ของเราสามารถแยกความถี่ที่ผสมกันอยู่ออกมาได้ นี่เป็นเพียงภาพง่าย ๆ ของกลไกแยกองค์ประกอบทางความถี่ ขณะที่ basilar membrane กับ cochlea มีความซับซ้อนมากกว่านี้เยอะ การเคลื่อนที่ของ basilar membrane ขึ้นอยู่กับความเฉื่อยของของเหลวที่อยู่รอบ ๆ, เรโซแนนซ์ใน tectorial membrane, stereocilia ของ outer hair cells และส่วนสำคัญคือ กิริยาเชิงกล (mechanical action) ของ outer hair cells (รายละเอียดส่วน outer hair cells ช่วย basilar membrane อย่างไร จะกล่าวถึงในบล็อกตอนอื่น) จากกลไกที่กล่าวมา ทำให้เราพูดได้ว่า basilar membrane ทำตัวเหมือนกับ band-pass filter หลาย ๆ อัน (bank) ที่มีช่วง bandwidth ความถี่ปล่อยผ่านซ้อนทับกัน ดังรูป 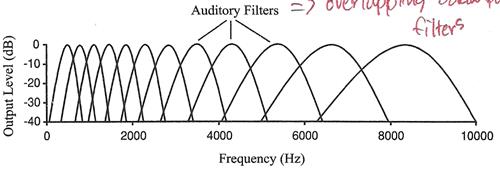แต่ละตำแหน่งบน basilar membrane มี characteristic frequency, bandwidth และ impulse response เฉพาะตัว ตอนที่เสียงซึ่งมีความถี่รวมกันแบบซับซ้อนเดินทางเข้ามาในหู องค์ประกอบความถี่สูงของเสียงนั้นจะกระตุ้น basilar membrane แถว ๆ base ขณะที่องค์ประกอบความถี่ต่ำจะกระตุ้นแถว ๆ apex ดังนั้น basilar membrane จึงเหมือนกับตัววิเคราะห์สเปกตรัมของเสียงที่เข้ามา ดังรูป characteristic frequency ของตำแหน่งต่าง ๆ บน basilar membrane ไม่ได้เปลี่ยนแปลงอย่างเป็นเชิงเส้นจาก base ถึง apex แต่ค่อนข้างเป็น logarithm นะครับ ความถี่สูงจะอยู่ใกล้ชิดกันมากกว่าความถี่ต่ำ ดังรูป The Traveling Wave ถึงแม้ basilar membrane จะมีขนาดเล็ก ส่วนที่กว้างที่สุดแค่ 0.45 มิลลิเมตรเท่านั้น แถมยังอยู่ในผนังแข็งคล้ายกระดูกของ cochlea แต่นักวิทยาศาสตร์ก็สามารถศึกษาการเคลื่อนที่ของ basilar membrane ในการตอบสนองต่อเสียงได้โดยตรงจากการผ่าตัด และคนแรกที่บุกเบิกเรื่องนี้คือ Georg von Békésy (ได้รับรางวัลโนเบลสาขาแพทย์ปี 1961 จากเรื่องนี้แหละครับ) เขาศึกษาการเคลื่อนที่ของ basilar membrane ใน cochlea ที่ตัดออกมาจากศพคนและสัตว์ อันที่จริงเขาดูการเคลื่อนที่ของอนุภาคเงินที่โปรยกระจายอยู่บน Reissner's membrane ซึ่งมันก็เคลื่อนที่ไปพร้อมกับโครงสร้างรอบ ๆ scala media รวมถึง basilar membrane และ organ of Corti ฉะนั้นการเคลื่อนที่ของอนุภาคเงินเหล่านี้ก็สามารถใช้บอกการเคลื่อนที่ของ basilar membrane ได้ด้วย von Békésy สังเกตว่า ถ้าเราป้อน pure tone เข้าหู รูปแบบลักษณะเฉพาะของการสั่นจะเกิดขึ้นบน basilar membrane ถ้าเรานึกภาพคลี่ cochlea ให้เป็นท่อตรงยาว การเคลื่อนที่ของ basilar membrane จะดูคล้ายคลื่นน้ำเดินทางจาก base ไปยัง apex รูปแบบการสั่นนี้เรียกว่า traveling wave ดังรูปข้างบน ถ้าเรามองตาม traveling wave จาก base ไปยัง apex เราจะเห็นว่าคลื่นค่อย ๆ โตขึ้นกระทั่งถึงจุดสูงสุด อันเป็นจุดบน basilar membrane ที่มีเรโซแนนซ์ที่ความถี่ของ tone ก่อนคลื่นจะเล็กลงและหายไปอย่างรวดเร็ว โปรดระลึกว่า คลื่น traveling นี้ เป็นผลสืบเนื่องจากการที่แต่ละตำแหน่งบน basilar membrane เคลื่อนที่ขึ้นและลงในการตอบสนองต่อการกระตุ้นด้วย pure tone โดยที่ความถี่ของการสั่นแต่ละตำแหน่งนั้นจะเท่ากับความถี่ของ pure tone เรื่องที่เข้าใจผิดกันบ่อยเรื่องหนึ่งคือ การเคลื่อนที่ของ traveling wave จาก base ถึง apex เป็นผลจากการเปลี่ยนแปลงความดันที่เข้ามายัง cochlea ผ่านหน้าต่างวงรีที่ base อันนี้ผิดนะครับ เพราะเสียงเคลื่อนที่เร็วมากในของเหลวใน cochlea ฉะนั้น ทุกจุดบน basilar membrane จึงได้รับการกระตุ้นแทบจะพร้อม ๆ กันตอนที่มีความดันเปลี่ยนแปลงเกิดขึ้นที่หน้าต่างวงรี การเคลื่อนที่แบบลักษณะเฉพาะดังกล่าวของ traveling wave เกิดขึ้นเพราะมีการหน่วงเฟส (phase delay) ที่เพิ่มขึ้นจาก base ถึง apex ทำให้ membrane ที่ apex สั่นช้ากว่าที่ base และการหน่วงนี้เป็นผลจากลักษณะทางกายภาพของ membrane ที่ส่วน base มีความแข็งทื่อและแคบกว่าส่วน apex (นั่นคือ ระบบ stiffness-limited จะตอบสนองเร็วกว่าระบบ mass-limited) รูปต่อไปนี้แสดง snapshot ของ membrane ขณะตอบสนองต่อ pure tone สองตัว ที่ความถี่ 2 kHz และ 200 Hz ตามลำดับ เห็นว่าช่วงความกว้างการตอบสนองของความถี่ต่ำบน membrane จะกว้างกว่าความถี่สูง (ดูความยาวของ envelope) เพราะแต่ละตำแหน่งบน basilar membrane จะทำตัวเหมือน band-pass filter ที่ย่านความถี่ผ่านแตกต่างกันไป ยิ่งความถี่ต่ำ ก็เหมือนมันผ่าน filter ได้เกือบทุกตัวบนด้วยการลดทอนที่ไม่เท่ากัน เราจึงเห็นจากรูปว่า basilar membrane เกือบทั้งสายตอบสนองต่อความถี่ต่ำ ขณะที่มีบริเวณช่วงไม่กว้างนักตอบสนองต่อความถี่สูง Transduction & How Do Inner Hair Cells Work? ภารกิจแปลงการสั่นของ basilar membrane ไปเป็นสัญญาณไฟฟ้าเพื่อส่งต่อให้สมองเป็นหน้าที่ของ inner hair cells ด้านบนของ hair cells มี stereocilia อยู่หลายแถว หน้าตาคล้ายขนเส้นเล็ก ๆ ตอนที่ basilar membrane กับ tectorial membrane เคลื่อนที่ขึ้นลงนั้น ขนพวกนี้จะถูกทำให้เอียงเฉียงด้านข้าง ดังรูป ในความเป็นจริง stereocilia เอียงแค่นิดเดียว (รูปที่เห็นถูกทำให้เว่อร์ไปนิดนะครับ) สำหรับเสียงระดับใกล้เคียงขีดเริ่มการได้ยิน พวกมันเอียงไปด้วยค่าการกระจัดแค่ 0.3 นาโนเมตรเท่านั้น พูดว่าถ้า stereocilia มีขนาดเท่ากับตึก Sears ในชิคาโก้ ระยะดังกล่าวก็เท่ากับการกระจัดของยอดแค่ 5 เซ็นติเมตร stereocilia แต่ละเส้นจะเชื่อมโยงกันด้วยเส้นใยโปรตีน เรียกว่า tip link ตอนที่ stereocilia เอียงเข้าหา scala media หรือชี้ออกนอก cochlea เส้นใย tip link นี้จะถูกดึงให้ยืด เปิดช่องเข้าเซลล์เล็ก ๆ ดังรูป ตอนที่ช่องนี้เปิดออกนั้น K+ (โปรตัสเซียมไอออน) จะไหลเข้าไปใน hair cell เพิ่มศักดาไฟฟ้าของเซลล์ (ในระดับ mV) และเนื่องจากศักดาไฟฟ้านิ่ง (resting electric potential) ของ inner hair cell มีค่าเป็นลบ (ประมาณ -45 mV) เราจึงเรียกการเพิ่มขึ้นของศักดาไฟฟ้าดังกล่าวว่า depolarization และกระบวนการ depolarization นี่เองที่ทำให้สารเคมีสื่อประสาท (neurotransmitter) ถูกปล่อยเข้าช่องเล็ก ๆ (synaptic cleft) ระหว่าง inner hair cell กับเซลล์ประสาทในเส้นประสาทรับรู้เสียง ดังรูป ตอนที่สารสื่อประสาทแพร่มาถึงเซลล์ประสาท (นิวรอน) มันจะทำให้เกิดพัลซ์กระแสไฟฟ้า (spike) ขึ้นในเซลล์ประสาท ถ้า stereocilia เอียงไปในทิศตรงข้าม หรือชี้เข้าหาศูนย์กลางของ cochlea นั่นคือ tip link คลาย ไม่ถูกดึง ทำให้ช่องทางดังกล่าวปิด ลดการปลดปล่อยสารสื่อประสาท ยิ่งการเคลื่อนที่ของ basilar membrane มากเท่าไร tip link ก็ยิ่งถูกดึงให้เปิดช่องกว้างมากขึ้นเท่านั้น และยิ่งมีการเปลี่ยนแปลงทางไฟฟ้าใน hair cell มาก สารสื่อประสาทก็จะยิ่งถูกปล่อยมาก สัญญาณไฟฟ้าในเส้นประสาทมากตามด้วย สำหรับ outer hair cell ก็ถูกกระตุ้นด้วยวิธีเปิดปิดช่องผ่านไอออนเช่นเดียวกับ inner cell แต่คิดกันว่า การเปลี่ยนแปลงศักดาไฟฟ้าของเซลล์นี้จะทำให้ความยาวของเซลล์เปลี่ยน ดังนั้นมันจึงก่อให้เกิดผลประทบต่อ basilar membrane (จะกล่าวถึงในบทต่อไป) ข้อสำคัญ outer hair cell ไม่ข้องเกี่ยวกับการส่งผ่านข้อมูลไปยังสมอง The Auditory Nerve คำถาม สัตว์ขนาดใหญ่จะส่งข้อมูลจากส่วนหนึ่งไปยังอีกส่วนหนึ่งของร่างกายได้อย่างไร คำตอบ ระบบประสาท ระบบประสาทประกอบด้วยเซลล์ประสาทหรือนิวรอนซึ่งทำหน้าที่ติดต่อสื่อสารอย่างรวดเร็วระหว่างเซลล์รับสัมผัส (sensory cell) เซลล์กล้ามเนื้อ และสมอง สมองคนเรามีนิวรอนมากกว่าหนึ่งแสนล้านเซลล์ แต่ละเซลล์มีการเชื่อมต่อกับเซลล์อื่นอีกนับร้อย นิวรอนกับการเชื่อมต่อนี่แหละครับเป็นโครงข่ายประมวลผลที่ซับซ้อนและมีกำลังมาก ถึงขั้นทำให้เราคิดได้ รู้สึกได้ และดูทีวีได้ 4 ส่วนประกอบหลักของนิวรอนได้แก่ dendrite, soma (ลำตัวเซลล์), axon กับ terminal button ดังรูป 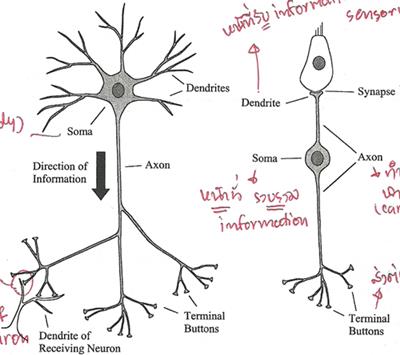รูปนี้แสดงให้เห็นโครงสร้างของนิวรอน 2 แบบ รูปซ้ายเป็นนิวรอนที่พบเห็นได้ในสมอง มี dendrite กับ terminal button หลายเส้น ที่มุมล่างซ้ายของรูปซ้ายแสดง terminal button สร้าง synapse กับ dendrite ของนิวรอนอื่น ส่วนรูปขวาเป็นนิวรอนรับสัมผัส เช่น ตัวที่เชื่อมต่อกับ hair cell ใน cochlea พวกนี้มี dendrite เดียว พูดคร่าว ๆ หน้าที่ของ dendrite คือ รับข้อมูลจากเซลล์รับสัมผัส อย่าง inner hair cell หรือจากนิวรอนตัวอื่น, soma รวบรวมข้อมูลข่าวสาร, axon นำพาข้อมูลข่าวสาร และ terminal button ส่งต่อข้อมูลให้กับ dendrite ของนิวรอนตัวอื่น synapse คือ การเชื่อมระหว่าง terminal button กับ dendrite หรือระหว่างเซลล์รับสัมผัสกับ dendrite โดยทั่วไปในสมองของเรา dendrite ของนิวรอนตัวหนึ่งจะสร้าง synapse กับ terminal button ของนิวรอนตัวอื่นอีกหลายร้อยตัว ความยาวของ axon อาจยาวได้เกือบ 1 เมตรในนิรอนที่เกี่ยวข้องกับการเคลื่อนไหวของกล้ามเนื้อ มันนำพาข้อมูลข่าวสารในรูปอิมพัลซ์ไฟฟ้า เรียกว่า action potential หรือ spike โดยขนาดของ spike คงที่ประมาณ 10 mV แต่รูปแบบของ spike หรือจำนวนความถี่ spike ต่อหน่วยเวลา หรือที่เรียกว่า firing rate จะขึ้นอยู่กับข้อมูลข่าวสาร อัตราเร็วของ spike ใน axon อาจสูงถึง 120 m/s การเปลี่ยนแปลงศักดาไฟฟ้าที่ terminal button อันเนื่องจากมี spike เดินทางมาถึงนั้น จะทำให้มีการปลดปล่อยสารสื่อประสาท ซึ่งจะแพร่กระจายผ่านช่อง synapse ระหว่างเซลล์ ยิ่งมี spike มาถึงถี่ขึ้น ก็ยิ่งปล่อยสารสื่อประสาทมากขึ้น เมื่อนิวรอนฝั่งรับตรวจจับสารสื่อประสาทนั้นได้ มันอาจจะทำให้เกิด spike ในตัวมัน (หรืออาจจะยับยั้ง spike ที่กำลังเกิดอยู่ในตัวมันก็ได้ แล้วแต่กรณี) นั่นคือ การสื่อสารดังกล่าวเป็นกระบวนการ electrochemical Activity in the Auditory Nerve เส้นประสาทการรับรู้เสียงคือกลุ่มของ axon (หรือใยประสาท) ที่เชื่อมกับ (หรือพูดว่า สร้าง synapse กับ) hair cell ในคนเรามีประมาณ 30,000 นิวรอน และเส้นใยประสาทเหล่านี้ส่วนใหญ่จะเชื่อมกับ inner hair cell โดยที่ inner hair cell แต่ละตัวจะเชื่อมกับ dendrite ประมาณ 20 เส้นใยประสาท เนื่องจาก inner hair cell แต่ละตัวติดกับตำแหน่งเฉพาะตำแหน่งใดตำแหน่งหนึ่งบน basilar membrane ดังนั้น นิวรอนแต่ละตัวในเส้นประสาทการรับรู้เสียงจึงนำพาข้อมูลเกี่ยวกับการสั่นของ basilar membrane ที่ตำแหน่งเพียงตำแหน่งเดียวใน cochlea ทีนี้ แต่ละตำแหน่งดังกล่าวอ่อนไหว (sensitive) ต่อความถี่ลักษณะเฉพาะที่เจาะจงค่าหนึ่ง ทำให้ เราพูดได้ว่านิวรอนแต่ละตัวก็อ่อนไหวต่อความถี่ลักษณะเฉพาะบางค่านั้นเช่นกัน รูปด้านล่างแสดงให้เห็นว่านิวรอนแต่ละตัวจะมีความอ่อนไหวลดลงอย่างรวดเร็วเมื่อความถี่เสียงที่มากระตุ้นออกห่างจากความถี่ลักษณะเฉพาะ 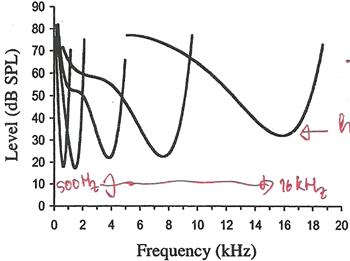กราฟในรูปนี้แสดงความสัมพันธ์ระหว่างระดับของ pure tone ที่ต้องป้อนเข้าหูเพื่อให้ firing rate ของนิวรอน 5 ตัว (แต่ละกราฟเป็นของนิวรอนคนละตัวกัน) เพิ่มขึ้นในปริมาณที่เริ่มตรวจวัดได้ เราเรียกกราฟนี้ว่า frequency threshold tuning curve (รูปมาจากเส้นประสาทรับรู้เสียงของหนู chinchilla) จุดต่ำสุด คือ จุดที่อ่อนไหวที่สุด ถึงแม้ไม่มีเสียง เส้นใยส่วนใหญ่ก็มี firing rate ระดับพื้น เรียกว่า spontaneous activity ซึ่งราว 90% ของเส้นใย จะมี spontaneous rate สูงประมาณ 60 spike ต่อวินาที เส้นใยเหล่านี้มีแนวโน้มค่อนข้างอ่อนไหวและเพิ่ม firing rate เมื่อถูกกระตุ้นที่ระดับต่ำ เส้นใยที่เหลืออีก 10% มี spontaneous rate ราว 10 spike ต่อวินาที เป็นพวกที่มีความอ่อนไหวน้อยกว่า ความอ่อนไหวที่แตกต่างกันนี้คาดว่าอาจสัมพันธ์กับตำแหน่งของ synapse กล่าวคือ ถ้า synapse อยู่ใกล้กับ outer hair cell มันจะเป็นเส้นใยที่มี spontaneous rate สูง แต่ถ้า synapse อยู่อีกด้านหนึ่ง จะมี spontaneous rate ต่ำ พอนิวรอนถูกกระตุ้นด้วย pure tone ที่ตรงกับความถี่ลักษณะเฉพาะของมัน firing rate จะเพิ่มขึ้นตามระดับของ tone จนถึงค่าสูงสุดค่าหนึ่ง เป็นจุดอิ่มตัว หมายความว่า ต่อให้ระดับของ tone จะเพิ่มมากกว่านี้ firing rate ก็ไม่เพิ่มไปมากกว่านี้ ดังรูป เราเรียกกราฟ rate-level function นอกจากนี้ เส้นใยประสาทยังแสดงการเปลี่ยนแปลง firing rate ในโดเมนของเวลาอันเนื่องมาจากการเริ่มต้นเสียง หรือ onset ดังรูป 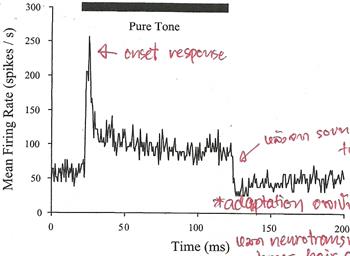เห็นว่า ตอนเริ่มต้นเสียง firing rate มีค่าสูงสุด (onset response) และลดลงเมื่อเวลาผ่านไป และพอปิดเสียง firing rate จะตกลงต่ำว่า spontaneous rate ราว 100 ms Place Coding เนื่องจาก firing rate ของนิวรอนในเส้นประสาทการรับรู้เสียงถูกกำหนดโดยขนาดการสั่นของ basilar membrane ณ ตำแหน่งที่มันเชื่อมอยู่ ดังนั้น นิวรอนแต่ละตัวในเส้นประสาทมีความถี่ลักษณะเฉพาะประจำตัว และพวกมันก็อ่อนไหวต่อช่วงความถี่จำกัดรอบ ๆ ความถี่ลักษณะเฉพาะนี้เท่านั้น นอกจากนี้ การเพิ่มระดับเสียง ยังเพิ่ม firing rate ของนิวรอน จนกว่าจะถึงจุดอิ่มตัว ฉะนั้น วิธีหนึ่งที่ระบบการรับรู้เสียงจะใช้แทนหรือนำเสนอสเปกตรัมของเสียงคือในรูปของ firing rate ของนิวรอนที่แตกต่างกัน เช่น ถ้าเสียงใดมีองค์ประกอบความถี่ต่ำอยู่ นิวรอนที่มีความถี่ลักษณะเฉพาะใกล้เคียงกับองค์ประกอบตัวนั้นจะเพิ่ม firing rate เราเรียกการนำเสนอข้อมูลสเปกตรัมแบบนี้ว่า place code หรือ rate-place code เพราะข้อมูลสเปกตรัมถูกแทนด้วยรูปแบบของ firing rate ของกลุ่มนิวรอน Phase Locking & Temporal Coding place coding มิได้เป็นเพียงวิธีการเดียวที่ characteristics ของเสียงจะถูกนำเสนอ การเปลี่ยนแปลงทางไฟฟ้าใน inner hair cell เกิดขึ้นเมื่อขนของมันเอียงชี้ไปทางด้านนอกของ cochlea เท่านั้น สมมติว่าตอนนี้ basilar membrane กำลังสั่นขึ้นลงตอบสนองต่อ pure tone ความถี่ต่ำ ขนหรือ stereocilia ของมันเอียงชี้สลับข้างไปมา ทีนี้ stereocilia จะเกิด depolarize ก็ต่อเมื่อมันเอียงไปทางด้านหนึ่งถูกมั้ยครับ นั่นเท่ากับ มันตอบสนองต่อบางเฟสเฉพาะของการสั่น หมายความว่า นิวรอนในเส้นประสาทการรับรู้เสียงจะผลิต spike ที่เฟสใดเฟสหนึ่งของ waveform สมบัตินี้เรียกว่า phase locking เพราะการตอบสนองของนิวรอนล็อกหรือจับคู่กับเฟสเฉพาะของการสั่น basilar membrane ดังรูป 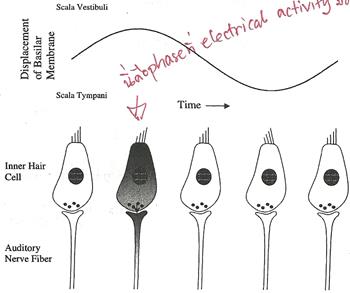จากรูป สีเทา คือ เฟสที่ electrical activity มีค่าสูงสุด จากสมบัติ phase locking นี่เอง ได้บอกเป็นนัยถึงอีกวิธีหนึ่งที่ใช้นำเสนอหรือใช้แทนความถี่ในเส้นประสาทการรับรู้เสียง นั่นคือ การนำเสนอในรูปของ timing หรือ synchrony ของกิจกรรมในเส้นประสาท เช่น ถ้าเรากระตุ้นด้วย pure tone ความถี่ 100 Hz พบว่า นิวรอนมีแนวโน้มที่จะผลิต spike อยู่ห่างกันเป็นจำนวนเต็มเท่าของคาบของ pure tone กรณีนี้คือ 10 ms ทีนี้ firing rate ของนิวรอนไม่อาจมากกว่า 200 spike ต่อวินาที นี่จึงดูเหมือนเป็นขีดจำกัดของการใช้ประโยชน์จาก phase locking อยู่ที่ความถี่ประมาณ 200 Hz อย่างไรก็ตาม ถึงแม้ว่าเส้นใยแต่ละตัวจะไม่สามารถตอบสนองด้วยอัตราที่สูงพอต่อการเป็นตัวแทนทุกรอบของ waveform ที่เป็นตัวกระตุ้น แต่สามารถแก้ปัญหาได้ด้วยการเอาข้อมูลข่าวสารจากนิวรอนทุกตัวมารวมกันเพื่อใช้แทนความถี่ของ tone ความถี่สูง ดังรูป ความถี่ของ input เท่ากับ 250 Hz รูปกลางเป็นรูปแบบ spike ของนิวรอนตัวเดียว รูปล่างเป็นการรวม spike ที่ผลิตจากนิวรอน 500 ตัว From Ear to Brain รูปต่อไปนี้แสดงเส้นทางส่งข้อมูลจากหูไปยังสมอง (ascending auditory pathways) เส้นประสาทนำข้อมูลจาก cochlea ส่งต่อไปยัง cochlea nucleus ซึ่งเป็นกลุ่มของนิวรอนใน brainstem (ก้านสมอง หรือ แกนสมอง) และส่งต่อไปยังนิวเคลียสต่าง ๆ ใน brainstem ดังรูป 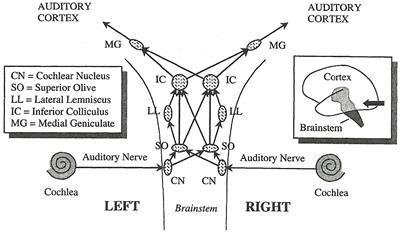แต่ละช่วงของการส่งนั้น ข้อมูลเกี่ยวกับเสียงจะถูกประมวลผลโดยโครงข่ายนิวรอน เช่น SO ประมวลผลเกี่ยวกับการบอกตำแหน่งของแหล่งกำเนิดเสียง และ IC เกี่ยวกับการรับรู้ pitch ของเสียง เส้นใยประสาทจาก IC เชื่อมกับ (หรือสร้าง synapse กับ) MG ซึ่งเป็นส่วนหนึ่งของทาลามัส (thalamus) ในสมองส่วนกลาง โดยทาลามัสทำตัวประหนึ่งชุมสาย (relay station) สำหรับข้อมูลรับสัมผัส เส้นใยประสาทจาก MG ต่อกับ auditory cortex (เปลือกสมองทำหน้าที่ด้านการรับรู้เสียง) ซึ่งเป็นส่วนหนึ่งของ cerebral cortex (เปลือกสมองใหญ่) cerebral cortex คือ ส่วนที่มองเห็นเป็นรอยยับย่นนั่นแหละครับ จะปกคลุมพื้นผิวส่วนใหญ่ของสมอง ทำหน้าที่ข้องเกี่ยวกับการประมวลผลความคิดในระดับสูง รวมถึงฟังก์ชั่นรับสัมผัสกับการเคลื่อนไหวเบื้องต้น cortex นี้เป็นแผ่นนิวรอนบาง ๆ ความหนาเพียง 3 มิลลิเมตร มันขดพับจนดูเป็นรอยยับเพื่อจะได้มีพื้นที่ผิวมาก บางส่วนของ cerebral cortex รับข้อมูลจากระบบประสาทรับสัมผัส มีส่วนรับรูป รับเสียง เป็นต้น ส่วนรับเสียง หรือ auditory cortex อยู่บน temporal lobe (สมองกลีบขมับ) ซ่อนอยู่ที่รอยย่นใน cerebral cortex ที่เรียกว่า Sylvian fissure (ร่องซิลเวียน) ดังรูป 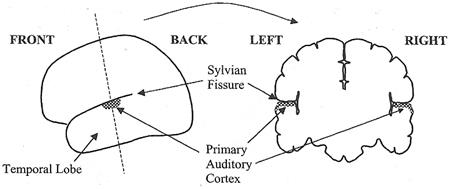นอกจาก ascending auditory pathways ยังมี descending pathways ซึ่งข้อมูลถูกนำส่งจากศูนย์กลางประมวลผลเสียงระดับสูงในสมองลงไปยังระดับต่ำกว่า และลงไปถึงกระทั่ง cochlea และสามารถควบคุมการเคลื่อนที่ของ basilar membrane ดูเหมือนว่าระบบรับรู้เสียงถูกออกแบบมาเพื่อให้ศูนย์ประมวลมวลผลระดับสูงสามารถควบคุมกิจกรรมในระดับต่ำ และส่งผลกระทบต่อการประมวลผลเสียงได้ด้วยครับ   Create Date : 30 เมษายน 2556     Last Update : 22 สิงหาคม 2556 22:17:07 น. Counter : 5400 Pageviews.   1 comment Share Tweet