|
Least Squares
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เป็นหลักการหนึ่งที่ใช้บ่อยใน DSP สมมติว่าเรามีฟังก์ชั่นต่อเนื่อง 2 ฟังก์ชั่น f(t) กับ f̂(c,t) เมื่อ c ไม่เป็นฟังก์ชั่นของ t ถ้าเราเลือก c ที่ทำให้ f̂(c,t) เป็นการประมาณแบบ least-squares ของ f(t) ในช่วง t1 ถึง t2 แล้ว total squared error (TSE) ซึ่งมีค่าตามสมการ
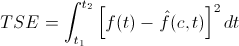
จะมีค่าต่ำสุด
ตัวอย่างรูปด้านล่าง f(t) เป็นคลื่นสามเหลี่ยมมีคาบ = 500 และพล็อตในช่วง t1 = 0 ถึง t2 = 1000 อีกฟังก์ชั่นหนึ่ง f̂(c,t) = c sin(2πt/500) ที่เลือกค่า c ให้ TSE ต่ำสุด เท่ากับเราพูดว่า f̂(c,t) เป็นการประมาณแบบ least-squares ของ f(t) ในช่วง [t1, t2] = [0, 1000]
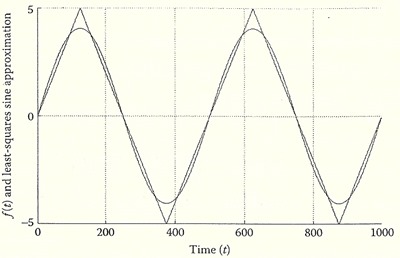
กรณีสัญญาณไม่ต่อเนื่อง f(t) จะกลายเป็นเวกเตอร์ที่มี elements เป็นแซมเปิ้ล N ตัว f = [f1 f2 ··· fN] และสมการ TSE เปลี่ยนเป็น
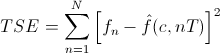
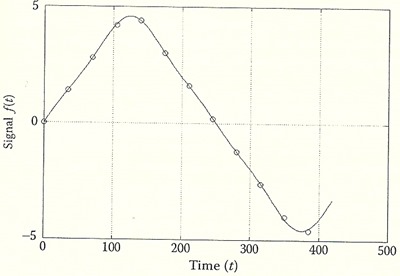
เมื่อ fn คือ element ที่ n ของ f และ T คือ time step หรือช่วงระหว่างแซมเปิ้ล ตัวอย่างรูปด้านล่างคือกรณีไม่ต่อเนื่องของรูปบนที่ T = 35, N = 28
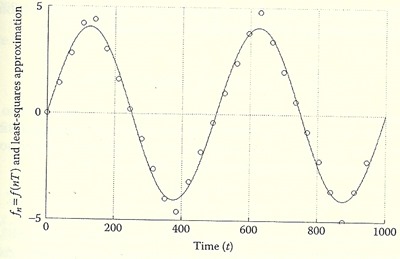
ถ้า f̂(c,t) เป็นฟังก์ชั่นเชิงเส้นของ c เช่น f̂(c,t) = c1 + c2t + c3t2 + ... + cMtM-1 เราจะเรียกว่าเป็นการประมาณแบบ least-squares ที่เป็นเชิงเส้น (linear least-squares approximation) ในกรณีดังกล่าว มีฟังก์ชั่นในรูป tm (ค่าของ m เริ่มจาก 0) อยู่ M ฟังก์ชั่น ถ้าให้ gm(t) เป็นฟังก์ชั่นของ t ฟังก์ชั่นที่ m เราจะเขียน gmn = gm(nT) แทนค่าของ gm(t) ที่ t = nT ฉะนั้น
f̂(c,nT) = c1g1n + c2g2n + c3g3n + ... + cMgMn
และ
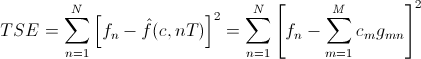
เงื่อนไขที่ทำให้ TSE ต่ำสุดคือ
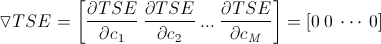
ทั้งหมดจะมี M สมการที่ต้องแก้ออกมาเพื่อหาเวกเตอร์ least-squares coefficient หรือ c = [c1 c2 ··· cM]′, เอาแบบไม่สนใจการจัดรูปทางคณิตศาสตร์นะครับ เราจะได้ c = (G′*G)∖(f*G)′ เมื่อ G = [G′1 G′2 ··· G′M], Gm = [gm1 gm2 ··· gmN], f = [f1 f2 ··· fN], '*' แทน การคูณเวกเตอร์, '′' แทน transpose และ '∖' คือ ตัวดำเนินการที่แก้ชุดของสมการเชิงเส้น เช่น ถ้า B = A∖C แล้ว A*B = C
ลองมาดูตัวอย่างกัน จากรูปบน เลือกมา 12 แซมเปิ้ล เราสร้างเป็น f = [f1 f2 ··· fN] ที่ N = 12 ได้ f = [0.0 1.4 2.8 4.2 4.4 3.0 1.6 0.2 -1.2 -2.6 -4.0 -4.6] คราวนี้ f̂(c,t) เราจะไม่ใช้แค่ฟังก์ชั่น sine ตัวเดียวเหมือนในรูปแล้ว แต่จะใช้ผลรวมของ sine สามตัวแทน
f̂(c,t) = c1sin(2πnT/500) + c2sin(6πnT/500) + c3sin(10πnT/500)
เมื่อ n = 0..11, gmn = sin(2π(2m-1)nT/500) ฉะนั้น เมตริกซ์ G มี 3 หลัก (M = 3) และ 12 แถว (N = 12) โค้ด MATLAB ต่อไปนี้ใช้สร้าง G
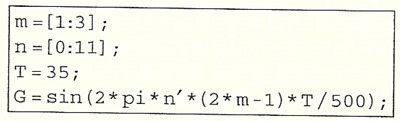
หลังจากได้ G12x3 เราก็คำนวณหา c ได้ตามสูตรครับ

ที่มา: หัวข้อ 2.2 Least Squares หนังสือ Digital Signal Processing with Examples in MATLAB ของ S. D. Stearns กับ D. R. Hush
| Create Date : 28 กรกฎาคม 2556 | | |
| Last Update : 28 กรกฎาคม 2556 16:33:55 น. |
| Counter : 1990 Pageviews. |
| |
|
 |
|
|
|
Correlation
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
correlation เป็นการวัดที่ใช้บอกว่า waveform (หรือ image) สองอันใด ๆ มีความเหมือนกันแค่ไหน, autocorrelation จะบอกว่า waveform ที่เวลา t เหมือนกับตัวมันเองที่เวลา t+τ แค่ไหน (หรือภาพที่ตำแหน่ง (x,y) กับภาพเดียวกันที่ตำแหน่ง (x+σ, y+σ))
ถ้า x(t) และ y(t) เป็น waveform สองอันที่นิยามในช่วง t = [0,∞) (หมายความว่า สัญญาณถูกนิยามจาก lower limit ถึงก่อน upper limit) ฟังก์ชั่น correlation ของ x และ y คือ
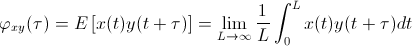
เมื่อ τ ≥ 0 และ E[·] แทนค่าคาดหมายหรือค่าเฉลี่ย, สำหรับกรณี waveform ไม่ต่อเนื่อง หน้าตาสมการจะเปลี่ยนไปเป็น
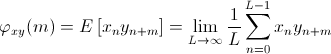
เมื่อ m ≥ 0 เป็น time shift ในหน่วยแซมเปิ้ล
จากนิยาม เห็นว่า correlation เป็นผลคูณเฉลี่ยของสัญญาณสองสัญญาณ ซึ่งผลคูณถูกเฉลี่ยโดยไม่มีขอบเขตบน ฉะนั้น ตราบเท่าที่ time shift เป็นบวก เราก็ไม่ต้องกังวลกับ end effects แต่ถ้า waveform ถูกนิยามในช่วงจำกัด [0, NT] เราจะเพิ่มเงื่อนไขหรือสมมติฐาน 2 ข้อต่อไปนี้ครับ
1. นอกช่วง [0, NT] ไม่มีสัญญาณ หรือพูดว่า ค่าของสัญญาณเท่ากับศูนย์
2. สัญญาณมีลักษณะเป็นคาบ ที่คาบ = NT
ตัวอย่าง correlation ของ waveform x กับ y แสดงดังรูป, x(t) เป็นสัญญาณสี่เหลี่ยม และ y(t) เป็นสามเหลี่ยม โค้ด MATLAB ด้านล่างคำนวณ φxy(m) โดยขยายคาบของ y (yy = [y,y]) ไม่ให้ yn+m หลุดขอบเวกเตอร์นะครับ
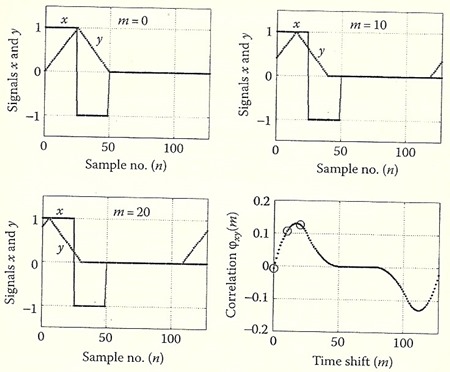

กราฟแสดงสัญญาณ x, y กรณี m = 0, m = 10 และ m = 20 ที่ xn อยู่ที่เดิม ขณะ yn+m (ซึ่งขยายให้เป็น yy) เลื่อนไปทางซ้าย โดย o ในกราฟ φxy(m) แสดง correlation ของทั้ง 3 กรณีดังกล่าว
correlation detection เป็นตัวอย่างการใช้ correlation ในงานประมวลผลสัญญาณ รูปด้านล่างแสดง target signal และ target signal ที่ผสมใน noise ที่ 1000 กับ 3700 ซึ่งถ้ามองแค่รูปกลางรูปเดียว เราอาจบอกไม่ได้ใช่มั้ยครับว่ามี target signal อยู่ตรงตำแหน่ง 1000 กับ 3700 นะ แต่เราก็สามารถตรวจจับ target signal ได้ง่ายโดยหา correlation ระหว่าง target signal กับ target signal + noise
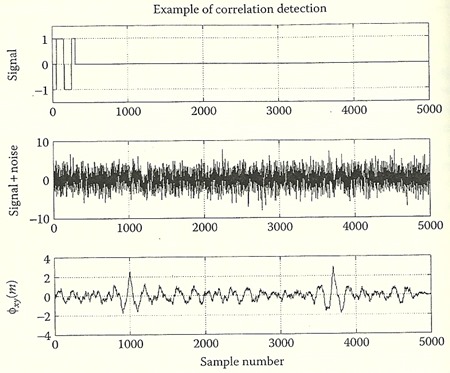
ที่มา: หัวข้อ 3.2 Correlation หนังสือ Digital Signal Processing with Examples in MATLAB ของ S. D. Stearns กับ D. R. Hush
| Create Date : 27 กรกฎาคม 2556 | | |
| Last Update : 27 กรกฎาคม 2556 21:23:13 น. |
| Counter : 1670 Pageviews. |
| |
|
| |
|
|
|
Data-hiding Scheme for Digital-Audio in Amplitude Modulation Domain
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ Nhut Minh Ngo, Masashi Unoki, Ryota Miyauchi กับ Yoiti Suzuki จาก 8th International Conference on Intelligent Information Hiding and Multimedia Signal Processing ปี 2012 ที่ Piraeus-Athens, Greece
เทคนิคและโครงสร้างหลักเหมือนกับ (1) Method of Digital-Audio Watermarking Based on Cochlear Delay Characteristics, (2) Reversible Watermarking for Digital Audio Based on Cochlear Delay Characteristics, (3) Detection of Tampering in Speech Signals with Inaudible Watermarking Technique ข้อแตกต่างคือการประยุกต์ใช้งานครับ จุดประสงค์ของบทความนี้คือ นำเสนอวิธีการซ่อนข้อมูลบางอย่างลงในสัญญาณที่กระจายเสียงผ่านระบบวิทยุ AM เพื่อให้ผู้รับฟังเฉพาะบางกลุ่มเท่านั้นที่สามารถถอดข้อมูลที่ซ่อนไว้ออกมาได้
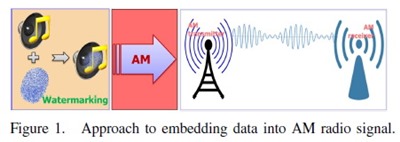
ในส่วนของการซ่อนข้อมูล (watermarking) ทำแบบเดิมเป๊ะ (ดูลิงค์ทั้ง 3 ในย่อหน้าแรก) หลังจากนั้นจึงเอา x(n) กับ y(n) ไปผ่าน double modulation ก่อนออกอากาศ ส่วนภาครับ ก็จะรับสัญญาณมาผ่าน double demodulation เพื่อให้ได้ x̂(n) กับ ŷ(n) แล้วก็เอาสัญญาณทั้งสองมาดึงลายน้ำหรือข้อมูลที่ซ่อนออกเหมือนเดิม (ระบบนี้จึงเป็นแบบ non-blind watermarking ครับ) ภาพรวมแสดงใน Figure 2. กับ 3.

ผมขอเล่าเฉพาะส่วนที่แตกต่างจากบทความก่อนหน้านะ นั่นคือ ขั้นตอน double modulation กับ demodulation ซึ่ง block diagrams ของพวกมันแสดงดัง Figure 4. กับ 5. ตามลำดับ
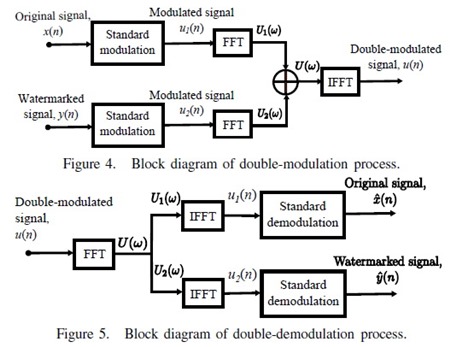
กล่อง standard modulation คือ AM technique ที่ใช้ในระบบวิทยุ AM แบบปกติทั่วไปนะครับ เริ่มจาก ภาค modulation เมื่อได้ x(n) และ y(n) มาแล้วก็เอาไป mod กับ carrier ธรรมดา ๆ ได้ u1(n) กับ u2(n) ตามลำดับ เมื่อเราดูสเปกตรัมของ u1(n) กับ u2(n) นะ เราจะเห็นว่าแต่ละอันมี sidebands 2 ฝั่ง ซ้าย-ขวาของความถี่ของคลื่น carrier เรียกฝั่งที่มีความถี่ต่ำกว่าว่า lower sideband และฝั่งที่ความถี่สูงกว่าว่า upper sideband (อันนี้เป็นผลที่เกิดขึ้นตามธรรมชาติของ AM) U1(ω) กับ U2(ω) เป็นสเปกตรัมของ u1(n) กับ u2(n) ซึ่งเราจะเลือกเอา lower sideband ของ U1(ω) กับ upper sideband ของ U2(ω) มารวมกันเป็น U(ω) แล้วแปลงอินเวิร์สฟูริเยร์ก่อนส่ง u(n) ออกอากาศ เป็นอันเสร็จสิ้นพิธี double modulation ในส่วน demodulation ก็แค่ทำย้อนกลับ (ดู Figure 5.) เริ่มจากสเปกตรัมของ u(n) คือ U(ω) เอามาแยก lower sideband เพื่อสร้าง U1(ω) และ upper sideband เพื่อสร้าง U2(ω) แต่ก่อนแปลงทั้งคู่ด้วย IFFT ไปเป็น u1(n) กับ u2(n) ตามลำดับ ก็อย่าลืม copy ส่วน lower sideband ของ U1(ω) ไปทางฝั่ง upper sideband ของมัน และ copy ส่วน upper sideband ของ U2(ω) ไปทางฝั่ง lower sideband ของมันเองก่อนด้วย ไม่อย่างนั้นพอผ่าน standard demodulation แล้วสัญญาณ output ที่ได้จะผิดเพี้ยน เท่านี้เราก็ได้ x̂(n) กับ ŷ(n) เพื่อนำไปป้อนต่อให้กับส่วนที่จะใช้ดึงลายน้ำหรือข้อมูลออกมาแล้วครับ
ผลการทดลอง ไม่มีอะไรแตกต่างจากการบทความก่อนหน้าชัดเจนนะครับ นอกจากจะสรุปเพิ่มเติมว่า CD-based method อันนี้สามารถนำไปใช้ใน AM ได้โดยปราศจากความผิดเพี้ยน บิตเรตในการซ่อนข้อมูลที่เหมาะสมอยู่ที่ 256 bps และถ้า noise ลดลงต่ำทำให้ SNR > 30 dB สมบัติ inaudibility จะดี และคุณภาพของเสียงลดลงถ้า b0 เพิ่มมากขึ้น (b1 = b0 + 0.07)
| Create Date : 27 กรกฎาคม 2556 | | |
| Last Update : 27 กรกฎาคม 2556 23:01:03 น. |
| Counter : 1727 Pageviews. |
| |
|
| |
|
|
|
|

