• ก็อยากจะเล่า
• หนังสือแนะนำ
• เกี่ยวกับศาสนา
• เรื่องที่น่าสนใจ
• หมากกระดาน
• อยากให้ลองฟัง
• ดูได้เรื่อยเรื่อย
• ห้องทดลองเขียน
• อิเล็กทรอนิกส์
• ภาษาต่างประเทศ
• ผู้คนที่น่าสนใจ
• matlab กับ [..]
• ในห้องของศล
• คลังวีดีโอคลิป
• เรื่องที่กำลังศึกษา

• Webmaster - BlogGang

• Deutsch-Englisch
• Latin Dictionary
• Babel Fish Translation
• พจนานุกรม
• Dictionary.com
• พจนานุกรมพุทธศาสน์
• CAMBRIDGE Dict.
• ศัพท์บัญญัติ
• วัดญาณเวศกวัน
• Oxford AL Dict.
• AT&T Natural Voices
• WordNet Online
• Etymology
• Catholic Encyclopedia
• Wolfram Alpha
• BlogGang.com

Hilbert-Huang Transform [สารบัญกลุ่มเรื่องที่กำลังศึกษา] HHT ถูกออกแบบมาเพื่อวิเคราะห์สัญญาณ nonstationary และ nonlinearity ประกอบด้วยส่วนสำคัญ 2 ส่วน คือ empirical mode decomposition (EMD) กับ Hilbert spectral analysis (HSA) โดย HHT จะใช้วิธี EMD ในการแยกสัญญาณออกเป็น intrinsic mode function (IMF) แล้วใช้ HSA ในการหาข้อมูล instantaneous frequency (HSA คือ วิธีวิเคราะห์สัญญาณที่ใช้การแปลงฮิลแบร์ตในการคำนวณ instantaneous frequency ของสัญญาณ) 1. การแปลงฮิลแบร์ตของ x(t) คือ y(t)            เมื่อ P คือ Cauchy principle value ของ singular integral และเราได้ analytic function z(t) = x(t) + iy(t) = a(t)eiθ(t) ค่าของ instantaneous amplitude a(t) = (x2 + y2)1/2 และ instantaneous phase θ(t) = tan-1(y/x) โดยอัตราการเปลี่ยนแปลง instantaneous phase ต่อเวลานี่แหละครับคือ instantaneous frequency ω = dθ/dt เนื่องจากทั้ง amplitude และ frequency เป็นฟังก์ชั่นของเวลา ดังนั้นเราสามารถเขียน amplitude (หรือพลังงานซึ่งก็คือแอมปลิจูดยกกำลังสอง) ในรูปของฟังก์ชั่นของเวลาและความถี่ H(ω,t) เรานิยาม marginal spectrum จาก            เมื่อข้อมูลดังกล่าวถูกนิยามในช่วงโดเมนเวลา [0,T] โดยค่า marginal spectrum บ่งบอกถึงแอมปลิจูด (พลังงาน) สะสมตลอดช่วงของข้อมูลในแง่ของโอกาส และยังเป็นวิธีการวัดแอมปลิจูด (หรือพลังงาน) รวมที่เป็นผลมาจากแต่ละค่าความถี่ ฉะนั้นจึงเป็นอีกทางเลือกหนึ่งในการแสดงสเปกตรัมของข้อมูลแทนการแสดงด้วยสเปกตรัมฟูริเยร์แบบเก่า ตัวอย่าง จากรูป (a) เส้นทึบสีน้ำเงินกับสีเขียวแสดง oscillatory function อย่างง่าย ตามสมการ            โดยเส้นสีน้ำเงินขี่บนค่าเฉลี่ย 0 ส่วนเส้นสีเขียว บนค่าเฉลี่ย 2 เส้นสีดำเล็ก ๆ เป็น upper กับ lower envelopes (b) เส้นสีดำคือ instantaneous frequency จริง ส่วนเส้นสีน้ำเงินกับเขียวคือ instantaneous frequency จากการแปลงฮิลแบร์ต (c) เส้นสีน้ำเงินแสดงสเปกตรัมฟูริเยร์ เส้นสีเขียวแสดง marginal spectrum 2. สมมติฐานของ EMD คือ ณ เวลาใด ๆ ข้อมูลอาจจะมี oscillatory modes อย่างง่ายของความถี่ที่แตกต่างกันอย่างมีนัยสำคัญอยู่ร่วมกัน ซ้อนทับกัน องค์ประกอบแต่ละตัวจะเรียกว่า IMF ซึ่งมีเงื่อนไขดังต่อไปนี้ (1) จำนวน extrema และจำนวน zero crossing ของทั้ง data set จะแตกต่างกันได้ไม่เกิน 1, (2) ณ จุดใด ๆ (data point) ค่าเฉลี่ยของ envelope ที่นิยามโดย local maxima และ local minima จะต้องเท่ากับ 0 ตัวอย่าง สัญญาณอินพุต x(t) คือ เส้นทึบในรูป a และ b โดยขั้นตอน sifting เริ่มด้วยการระบุ local extrema ทั้งหมด ในรูป b ใช้สัญลักษณ์ข้าวหลามตัดระบุจุด maxima และใช้สัญลักษณ์วงกลมระบุจุด minima แล้วลากเส้น cubic spline เชื่อม local maxima ทั้งหมดเข้าด้วยกันเพื่อให้ได้ upper envelope และเชื่อม local minima ด้วยเส้น cubic spline ได้ lower envelope ดังรูป c ซึ่งโดยทั่วไปข้อมูลทั้งหมดจะถูกตีกรอบด้วย 2 เส้นนี้นะครับ จากนั้น หาเส้น m1 หรือเส้นประตามรูป c เป็นเส้นที่เป็นค่าเฉลี่ยของ upper กับ lower envelope ผลต่างระหว่างอินพุต x(t) กับ m1 คือ protomode แรก เขียนแทนด้วย h1 ดังรูป d           h1 = x(t) - m1 h1 ถือว่าเป็น proto-IMF ที่จะเอามาวนลูปทำซ้ำ h1 - m11 = h11 หลังจากทำซ้ำไป k ครั้ง h1(k-1) - m1k = h1k เราได้ h1k ที่สอดคล้องกับเงื่อนไขของการเป็น IMF (ดังรูป e, ส่วนรูป f คือผลลัพธ์จากการลบรูป a ด้วยรูป e) มันก็จะกลายเป็น IMF c1 = h1k เงื่อนไขการหยุดมีหลายแบบนะครับ เช่น ผลต่าง normalized squared ระหว่างการทำ sifting 2 รอบที่ติดกัน ซึ่งนิยามจาก            จะต้องน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าค่าหนึ่ง ตัวอย่าง SDk ที่แตกต่างอีกอัน (ซึ่งจะต้องน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าเช่นกัน) เช่น            เงื่อนไขการหยุดดังกล่าว เราเรียกว่าเป็นแบบ Cauchy types นะครับ ถึงแม้จะดู rigorous ในทางคณิตศาสตร์ แต่ในทางปฏิบัติ implement ได้ยาก เพราะ ตรงที่บอกว่าน้อยกว่าค่าที่กำหนดไว้ล่วงหน้าค่าหนึ่งนี่ คำถามคือ ค่าไหน? อีกอย่าง ผลต่างกำลังสองอาจจะมีค่าน้อย แต่มันก็ไม่ได้รับประกันว่าจำนวน zero crossing กับ extrema จะเท่ากัน Huang จึงได้เสนอเงื่อนไขการหยุดอีกแบบ เรียกว่าการหยุดแบบ S (S stoppage) ซึ่งกระบวนการ sifting จะหยุดก็ต่อเมื่อ (1) จำนวนของ zero crossing กับ extrema แตกต่างกันไม่เกิน 1 และ (2) มีค่าเท่าเดิม S รอบติดกัน ค่า S ที่ Huang เสนอคืออยู่ระหว่าง 3 ถึง 8 IMF แรกควรจะมีส่วนที่สั่นด้วยคาบสั้นที่สุด (shortest-period oscillation) ในสัญญาณ เมื่อนำไปลบออกจากสัญญาณจะได้ residue r1 = x(t) - c1 ซึ่งมีการสั้นด้วยคาบที่ยาวกว่า เราก็ใช้ residue นี่แหละครับเป็น data ใหม่ เอาไปผ่านกระบวนการ sifting เหมือนเดิมเพื่อให้ได้ IMF ของความถี่ต่ำกว่า การเอา residue ไปทำซ้ำนี้ เราจะหยุดเมื่อ rn กลายเป็น monotonic function หรือเป็นฟังก์ชั่นที่มี extremum เดียว ซึ่งไม่อาจถอด IMF ออกมาได้อีก           r1 - c2 = r2           ...           rn-1 - cn = rn ฉะนั้นเราได้            ข้อมูลต้นฉบับ x(t) แยกออกมาเป็น IMF จำนวน n ตัว และ final residue rn ตัวอย่างแสดงดังรูปด้านล่าง เป็นการแยกข้อมูลจาก Remote Sensing System (RSS) T2 ตามรูป a ออกเป็น IMF รูป b - h จากความถี่สูงไปต่ำ ถ้า x(t) เป็น time series ความยาว N เมื่อเอามาแยกด้วย EMD และหา instantaneous frequencies กับ instantaneous amplitudes ของแต่ละ IMF เราสามารถเขียนแทน x(t) ด้วย            เมื่อ Re[ ] แทนส่วนจริงของพจน์ที่อยู่ใน [ ] ในที่นี้เราตัด rn ทิ้งเพราะมันเป็น monotonic function หรือเป็นฟังก์ชั่นที่มี extrema เดียวซึ่งมีข้อมูลไม่เพียงพอที่จะยืนยันว่ามันเป็น oscillatory component ความถี่ของมันมีความหมายทางกายภาพ เห็นว่าทั้งแอมปลิจูดและความถี่ของแต่ละ component ในสมการนี้เป็นฟังก์ชั่นของเวลา ซึ่งการกระจายข้อมูลแบบฟูริเยร์ของข้อมูลชุดเดียวกันนี้จะอยู่ในรูป            โดยที่ทั้ง aj และ ωj เป็นค่าคงที่ เมื่อเปรียบเทียบ 2 สมการ จะเห็นว่า IMF เป็นการแสดงถึงการกระจายฟูริเยร์ในกรณีทั่วไป แอมปลิจูดที่เปลี่ยนค่าได้และ instantaneous frequency ไม่เพียงพัฒนาประสิทธิภาพของการกระจาย แต่ยังทำให้การกระจายเหมาะสำหรับข้อมูลที่ไม่เป็นเชิงเส้นและเปลี่ยนแปลงแบบ nonstationary HHT เป็นอีกทางเลือกหนึ่ง (และอาจเป็นทางเลือกที่มีความหมายทางกายภาพมากกว่า) ในการแทนข้อมูล เหตุผลคือ มันสามารถใช้ instantaneous frequency ในการบรรยาย intrawave frequency modulation นิยามของความถี่แบบปกติทั่วไปนันคือ ω = 1/T เมื่อ T คือ คาบของการสั่นใช่มั้ยครับ ถึงแม้นิยามนี้จะเป็นมาตรฐาน แต่มันก็ยังหยาบและไม่ครอบคลุม intrawave frequency modulation ซึ่งเป็นส่วนสำคัญของการสั่นแบบไม่เป็นเชิงเส้น ตัวอย่างความล้มเหลวดังกล่าวสามารถแสดงได้โดยด้วยสมการ Duffing            เมื่อ ε, γ และ α เป็นค่าคงที่, พจน์กำลังสามในสมการ Duffing ทำให้เกิดความไม่เป็นเชิงเส้น และเมื่อเราจัดรูปสมการใหม่            เห็นได้ชัดว่าพจน์ในวงเล็บสามารถตีความเป็นค่าคงที่สปริงที่ไม่คงที่ (a variable spring constant) หรือความยาวของลูกตุ้มที่เปลี่ยนค่าได้ (varying pendulum length) (นึกถึงสมการการเคลื่อนที่ของสปริงที่อธิบายด้วย nonhomogeneous differential) ไม่ว่าจะยังไงความถี่ก็เปลี่ยนในหนึ่งคาบ ซึ่ง intrawave frequency modulation ก็คือ harmonics ในมุมมองแบบเก่า และ Huang แย้งว่าการแสดงด้วย harmonic เป็นสิ่งที่สร้างขึ้นมาในทางคณิตศาสตร์ (a mathematical artifact) โดยมีความหมายทางกายภาพน้อยนิด ขณะที่ instantaneous frequency มีความหมายทางกายภาพมากกว่า และไม่เพียงสามารถใช้บรรยายการเปลี่ยนแปลง interwave frequency เนื่องจาก nonstationary เท่านั้น ยังใช้บรรยาย intrawave frequency modulation เนื่องจาก nonlinearity ได้ด้วย เปรียบเทียบการวิเคราะห์ฟูริเยร์ เวฟเล็ต กับ HHT แสดงดังตาราง ที่มา: เก็บความจากหัวข้อ A Brief Description of HHT ใน A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies โดย Norden E. Huang กับ Zhaohua Wu   Create Date : 16 กรกฎาคม 2556     Last Update : 16 กรกฎาคม 2556 22:19:09 น. Counter : 2719 Pageviews.   0 comment Share Tweet

Research of Improved Echo Data Hiding: Audio Watermarking based on Reverberation [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ G. Nain, S. Wang กับ Y. Ge ใน Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 117-180 ปี 2007 ที่ Honolulu เทคนิค echo-hiding ที่ผมได้เล่ามาหลายตอนก่อนหน้านี้ อย่างมากเราเพิ่ม echo เข้าไปไม่เกิน 4 ลูกใช่มั้ยครับ แต่สำหรับเทคนิคที่ผ้เขียนเสนอในบทความนี้ คีย์เวิร์ดของมันคือ reverberation ซึ่งก็ไม่ใช่อะไรหรอก นอกจาก echo จำนวนมากที่ผสมปนเปกันแบบซับซ้อน เรายังคงใช้ kernel 2 ตัวในการฝัง "0" กับ "1" แต่คำถามอยู่ที่ เราจะหา kernel ยังไง นี่แหละครับประเด็น และคำตอบของผู้เขียนคือ หาจาก reverberation (หรือพูดให้เจาะจง room impulse response) ที่จุด 2 จุดในห้อง ใช้จุดหนึ่งแทนการฝัง "0" และอีกจุดสำหรับฝัง "1" โดยวิธีการหา room ir ของผู้เขียนคือ image method และพารามิเตอร์ที่ใช้หา room ir ยังทำหน้าที่เป็น secret key ที่จำเป็นต้องใช้ในการดึงลายน้ำออกมา นั่นเท่ากับเป็นการเพิ่ม security อีกทอดหนึ่ง สมมติว่าแหล่งกำเนิดเสียงอยู่ที่ (sx, sy, sz) และเลือกผู้ฟัง 2 จุด พิกัด (lx1, ly1, lz1) กับ (lx2, ly2, lz2) คำนวณ room ir h1(n) กับ h2(n) จากนั้นใช้มันสร้าง kernel function f1(n) = δ(n) + h1(n) กับ f2(n) = δ(n) + h2(n) ซึ่ง room ir จะอยู่ในรูป h(n) = α1δ(n-n1) + α2δ(n-n2) + ... + αLδ(n-nL) เมื่อ L คือ ความยาวของ room ir (หรือจำนวน echo นั่นแหละครับ) ถ้า xi(n) คือ สัญญาณต้นฉบับ เราจะได้สัญญาณที่ฝังลายน้ำ xwi(n) = xi(n)*f(n) เมื่อสัญลักษณ์ * แทน linear convolution ตรงนี้เห็นว่า ขั้นตอนต่าง ๆ เหมือนเทคนิคในตระกูล echo-hiding ทั่ว ๆ ไป ต่างกันแค่วิธีการหา kernel function เท่านั้นเอง block diagram ขั้นตอนการดึงลายน้ำออกมาแสดงดังรูป จากรูป หลังหา cepstrum ของ xwi(n) แล้ว ก็เอา cepstrum นั่นมาหา cross-correlation กับ h1(n - n11 กับ h2(n - n21 ถ้าหากบิตที่ฝังอยู่คือ "1" เราจะเห็น peak ที่ n1 ของ d1(n) แต่ไม่เห็นของ d2(n) ดังรูป ถ้า σwn1 เป็น ส่วนเบี่ยงเบนมาตรฐานของ d1(n) ยกเว้นค่าที่ n1(n) เนื่องจากที่ตำแหน่งดังกล่าวเป็นค่า peak และ σwn2 เป็น s.d. 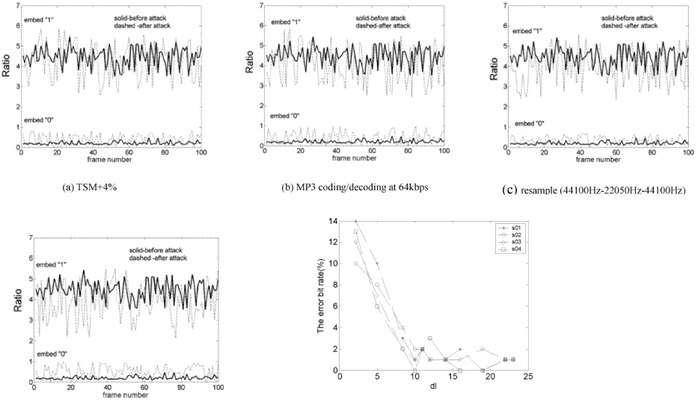ของ d2(n) ยกเว้นที่ค่าสูงสุดเช่นกัน เราจะใช้ค่า r(i) = [d1(max)/σwn1]/[d2(max)/σwn2] เป็นตัวตัดสินใจว่าบิตที่ฝังคือ "0" หรือ "1" ถ้า r(i) > T (เป็น threshold ค่าหนึ่ง) เราจะบอกว่าบิตที่ฝังอยู่คือ "1" แต่ถ้า r(i) < T บิตที่ฝังคือ "0" ผลการทดลอง: รูปด้านล่างแสดงความสัมพันธ์ระหว่าง dl = sqrt[(lx1-lx2)2 + (ly1-ly2)2 + (lz1-lz2)2] กับ correct response ของเพลง S01 - S04 เห็นว่า ยิ่ง dl น้อย correct response จะยิ่งดี และสมบัติ imperceptibility จะดีมากถ้า dl < 15 การทดลองที่เลือกใช้ dl = 8.378 เมื่อผ่านการโจมตีแบบต่าง ๆ แล้วพบว่า error bit rate < 4% กราฟด้านล่างแสดง ratio curve ก่อนและหลังการโจมตี   Create Date : 16 กรกฎาคม 2556     Last Update : 16 กรกฎาคม 2556 9:29:39 น. Counter : 1019 Pageviews.   0 comment Share Tweet

Researches on Echo Kernels of Audio Digital Watermarking Technology Based on Echo Hiding [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ X. Cao กับ L. Zhang ใน IEEE International Conference on Wireless Communications and Signal Processing ปี 2011 ที่ Nanjing จะว่าไป บทความนี้แตกต่างจากเทคนิคอื่น ๆ ในตระกูล echo-hiding ก็แค่เปลี่ยนหน้าตาของ kernel เท่านั้นเองครับ และเมื่อดูผลการทดลอง ก็ให้ความรู้สึกไม่แฟร์สักเท่าไร เพราะตัวที่ผู้เขียนใช้เทียบเคียงด้วยเป็น kernel ของ Bender ตั้งแต่ปี 1996 หน้าตาของ kernel ที่ Cao เสนอเป็นแบบนี้ เห็นว่าแตกต่างจาก mirrored kernel ของ Wu เพราะโครงสร้างของ kernel ที่ใช้ฝัง "0" กับ "1" ไม่เหมือนกัน (สังเกต positive echo ที่อยู่ใกล้ไกลกว่า negative echo เมื่อเทียบกับสัญญาณต้นฉบับ) ตัวอย่าง real cepstrum ของ segment ที่ฝัง "0" และ "1" ตามลำดับแสดงดังรูป โดย d0 = 40 แซมเปิ้ล และ d1 = 90 แซมเปิ้ล ผู้เขียนได้ทดสอบสองอย่าง คือ robustness test กับ subjective quality test และดูผลการเปลี่ยน α ที่กระทบต่อ detection rate เปรียบเทียบระหว่าง kernels ใหม่ที่นำเสนอกับ kernels ของ Bender ผลลัพธ์แสดงดังกราฟ การโจมตีและผลลัพธ์แสดงดังตาราง (แน่นอนว่ามันพัฒนาขึ้น) SDG เฉลี่ยก็ออกมาดีนะครับ แต่อย่างว่า แอบดูเหมือนไม่แฟร์ เพราะเทียบข้ามรุ่นแบบห่างกันเกินไป   Create Date : 15 กรกฎาคม 2556     Last Update : 15 กรกฎาคม 2556 22:03:21 น. Counter : 863 Pageviews.   0 comment Share Tweet

Analysis-by-Synthesis Echo Hiding Scheme Using Mirrored Kernels [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ ผมสรุปจากบทความในชื่อเดียวกันของ W. Wu กับ O. Chen จาก IEEE International Conference on Acoustics, Speech and Signal Processing ปี 2006 ที่ Toulouse ผมขอเล่าเฉพาะส่วนที่ผู้เขียนนำเสนอแตกต่างจาก echo-hiding แบบอื่น ๆ ซึ่งเคยพูดถึงไปแล้วในบล็อกหลายตอนก่อนหน้า งานชิ้นนี้ของ Wu มีคีย์เวิร์ดอยู่ 2 คำครับ คือ (1) analysis-by-synthesis กับ (2) mirrored kernels ขอเริ่มจากคำหลังก่อน mirrored kernels แสดงได้ดังรูป สำหรับ segment ใด ๆ ที่เราจะใส่ echo เราจะเอามันมาแบ่งเป็น 2 segments ย่อย เรียกว่า ท่อนหน้า (front part) กับท่อนหลัง (rear part) แต่ละท่อนจะใช้ kernel โครงสร้างเหมือนกันแต่มีพารามิเตอร์แตกต่างกัน เช่น รูป (a) ท่อนหน้าใช้พารามิเตอร์ da ขณะที่ท่อนหลังใช้พารามิเตอร์ db เพื่อแสดงถึงการฝัง "0" และถ้าหากเราอยากฝัง "1" เราก็แค่สลับให้ท่อนหน้าใช้พารามิเตอร์ db ส่วนท่อนหลัง da อันนี้แหละครับความหมายของชื่อ mirrored ของมัน ผู้เขียนอ้างว่า การทำ mirror จะเพิ่ม recovery rate ดูตารางผลการทดลองเปรียบเทียบ ค่า αe คือ equivalent decay rate ในกรณีของ EHBF คำนวณจาก αe = αb + αf ส่วนกรณี mirrored คำนวณจาก αe = (α0f + α0r + α1f + α1r)/2 คีย์เวิร์ดอีกคำ analysis-by-synthesis เป็นขั้นตอนที่เกิดขึ้นในกระบวนการฝังลายน้ำ ดังรูป หลังจากที่ได้ y[n] ตามการทำ echo แบบเดิม เราก็อย่าเพิ่งส่งมันนะครับ ยังไม่เสร็จพิธี ให้ป้อนมันเข้า noise model เพื่อจำลองการโจมตีแล้วเอาผลลัพธ์จากการโจมตีคือ ŷ[n] มาถอดดูว่าถอดได้หรือไม่ สมมติว่าข้อมูลที่เราฝังคือ I และถอดได้ Î ให้ตรวจสอบความถูกต้องโดยรวม Î กับ -I ถ้าผลลัพธ์ที่ได้ไม่เท่ากับ 0 (หมายความว่า ข้อมูลที่ดึงออกมาไม่ถูกต้อง) ก็ให้กลับไปปรับค่า α ใหม่ จนกว่า Î - I = 0 เราจึงจะพอใจ นี่ก็ตรงตามชื่อ analysis-by-synthesis นั่นแล ตารางผลด้านล่างแสดงให้เห็นว่าวิธีที่ Wu เสนอช่วยเพิ่ม robustness ของระบบ   Create Date : 15 กรกฎาคม 2556     Last Update : 15 กรกฎาคม 2556 21:17:54 น. Counter : 1024 Pageviews.   0 comment Share Tweet

A Novel Echo-Hiding Scheme with Backward and Forward Kernels [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทความในชื่อเดียวกันของ H.J. Kim กับ Y.H. Choi ตีพิมพ์ใน IEEE Transactions on Circuits and Systems for Video Technology, vol. 13, no. 8, pp. 885-889 ปี 2003 ข้อเสนอ B&F Kernels ของคิมนี้เป็นข้อเสนอที่ถูกอ้างถึงบ่อย ไอเดียของ Kim พัฒนามาจากของ Bender (1996) กับ Oh (2001) แบบง่าย ๆ ครับ คือ แทนที่จะใช้ kernel ซึ่งมี echo เดียว หรือ echo 2 ตัวที่เป็นบวกกับลบ (ดูรูป Fig.1 กับ Fig.2) เขาก็ใช้ kernel ที่มี echo ที่เป็นบวก 2 ตัว โดยตัวหนึ่งเกิดขึ้นก่อนสัญญาณและอีกตัวหนึ่งเกิดขึ้นหลังสัญญาณ (Fig.3) สำหรับ kernel แบบแรกของ Bender มีผลตอบสนอง impulse: h[n] = δ[n] + αδ[n-d] เมื่อ δ คือ Kronecker delta function, α เป็น decay rate เป็นพารามิเตอร์ตัวหนึ่ง และ d คือ delay offset สำหรับแบบ dual kernel ของ Oh นั้น h[n] = δ[n] + α1δ[n-d1] - α2δ[n-d2] h[n] ของ Kim คือ δ[n] + αδ[n-d] + αδ[n+d], คำถาม ทำแบบ Kim มีข้อดียังไง? Kim ได้พิสูจน์ให้เห็นในทางคณิตศาสตร์ว่า kernel ของเขาช่วยให้ recovery rate เพิ่มขึ้น เพราะขนาดของสัญญาณหลังการแปลง cepstrum ที่เวลา offset delay มีค่าสูงขึ้น เมื่อเทียบกับ 2 แบบแรก ลองดูสมการกันสักนิดนะ สัญญาณเสียง x[n] ป้อนเข้า kernel ที่มี impulse response h[n] ได้สัญญาณเสียงที่ใส่ echo เข้าไปแล้วคือ y[n] = x[n]*h[n] (เครื่องหมาย * แทนการ convolute) ต่อมา ในการตรวจจับเวลา delay ของ echo นั้น เราจะใช้วิธีหา cepstrum ของ y[n] เขียนแทนด้วย cy[n] = F-1(ln F(y[n])) เมื่อ F-1 และ F คือ การแปลงฟูริเยร์ผกผันและการแปลงฟูริเยร์ตามลำดับ จาก y[n] = x[n]*h[n] หรือ F(y[n]) = F(x[n]*h[n]) = F(x[n])·F(h[n]) = X(ejω)·H(ejω) ดังนั้น เราจะได้ cy[n] = F-1(ln X(ejω)) + F-1(ln H(ejω)) กรณี kernel ของ Bender นั้น H(ejω) = 1 + αe-jωd หรือ ln H(ejω) = αe-jωd - (α2/2)e-2jωd + (α3/3)e-3jωd - ... (เราใช้การกระจายอนุกรมกำลังของ ln(1 + x) = x - x2/2 + x3/3 - ...) แปลงกลับ ได้ ch[n] = αδ[n-d] - (α2/2)δ[n-2d] + (α3/3)δ[n-3d] - ... หรือ cy[n] = cx + αδ[n-d] - (α2/2)δ[n-2d] + (α3/3)δ[n-3d] - ... เห็นได้ชัดจากสมการนี้ว่า cepstrum ของ kernel จะทำให้เกิด pulse ซ้ำ ๆ กันที่ระยะห่างออกไปทีละ d และ peak แรกของ echo มีขนาดเท่ากับ α แต่ถ้า h[n] = δ[n] + αδ[n-d] + αδ[n+d] เราจะได้ H(ejωd) = 1 + αe-jωd + αe+jωd = 1 + 2α cosωd (จาก eiθ = cosθ + i sinθ) เมื่อกระจายอนุกรมกำลังแบบเดิมนะครับ ได้ ch[n] = 2α cosωd - (2α cosωd)2/2 + (2α cosωd)3/3 - ... โดยมีเงื่อนไขอนุกรมลู่เข้าคือ |2α cosωd| < 1 ฉะนั้น ch[n] = α{δ[n-d] + δ[n+d]} - (α2/2){δ[n-2d] + 2δ[n] + δ[n+2d]} + (α3/3){δ[n-3d] + 3δ[n-d] + δ[n+d] + δ[n+3d]} - ... จากสมการนี้ peak ของ cepstrum ที่ n = d เท่ากับ α + α3 + α5 + ... หรือประมาณ a = α/(1-α2) ซึ่งในกรณีที่ a2 < 1 นั้น a จะมากกว่า α นี่จึงเป็นเหตุผลที่ Kim อ้างว่าวิธีของเขาดีกว่า ดังแสดงในตาราง และรูปตัวอย่างด้านล่าง Kim อธิบายต่อว่า กรณี h[n] = δ[n] + αδ[n-d1] + αδ[n+d2] ที่ d1 ≠ d2 นั้น เราจะไม่มีทางได้ α/(1-α2) นั่นคือ ขนาดของ cepstrum จะดีขึ้นกรณีที่ kernel สมมาตร หรือ d1 = d2 เท่านั้น ความสูงของ cepstrum ขึ้นอยู่กับปัจจัย 3 ประการ ได้แก่ cepstrum response ของ echo kernel และของสัญญาณต้นฉบับ กับ echo kernel delay กระนั้น Kim ก็ไม่ได้อ้างว่า kernel ของเขาใช้การได้ดีในทุกกรณีนะครับ โดยเฉพาะเมื่อ x[n] เป็น monophonic ดังจะได้เห็นจากผลการทดลองต่อไป เพลงที่ Kim เลือกใช้ในการทดลองแสดงดังตารางด้านล่าง เขาเลือกคลิปเสียงอัตราสุ่ม 44.1 kHz 16 bits แบ่งเป็น segment ขนาด 4410 แซมเปิ้ล แต่ละ segment ก่อนนำมาฝังข้อมูลก็ให้มันผ่านหน้าต่าง Hanning โดยกำหนด delay = 100 แซมเปิ้ลแบบสมมาตรสำหรับฝัง "1" และ 103 แซมเปิ้ล สำหรับ "0" จากตาราง 01.wav - 03.wav เป็นเพลงที่ซ่อนลายน้ำได้ง่าย เพราะเป็นเพลงที่มีพลังงานสูง ขณะที่ 04.wav กับ 05.wav ซ่อนได้ยากกว่า โดยเฉพาะ 04 มีเสียงเครื่องดนตรีโบราณของญี่ปุ่นเป็นหลัก ซึ่งเป็นเสียง monophonic ผลลัพธ์จากการทดลองแสดงค่า dectection error rate (= จำนวนบิตที่ผิด/จำนวนบิตที่ฝัง) แสดงดังตารางด้านล่างเมื่อผ่านการโจมตีแบบต่าง ๆ ที่ค่า α = 0.2 และ 0.4 ตามลำดับ สังเกตกรณีของ 04.wav นะครับ นอกจากนี้ ผู้เขียนยังได้เสนอให้ฝังลายน้ำด้วยเทคนิค 2 แบบที่อ่อนไหวต่อการโจมตีแตกต่างกัน เพื่อเพิ่มโอกาสรอดของลายน้ำ   Create Date : 15 กรกฎาคม 2556     Last Update : 15 กรกฎาคม 2556 20:52:43 น. Counter : 1262 Pageviews.   0 comment Share Tweet