|
|
|
High Capacity Audio Watermarking Using the High Frequency Band of Wavelet Domain
เนื้อหาตอนนี้ สรุปจากบทความชื่อเดียวกันของ Mehdi Fallahpour กับ David Megias ตีพิมพ์ใน Multimedia Tools and Application Vol 52 Issue 2-3 หน้า 485-498 ปี 2011 วิธีการที่ผู้เขียนนำเสนอนี้ high capacity สมชื่อครับ เพราะสามารถซ่อนข้อมูลลงในเสียงได้ถึง 11 kbps !!!
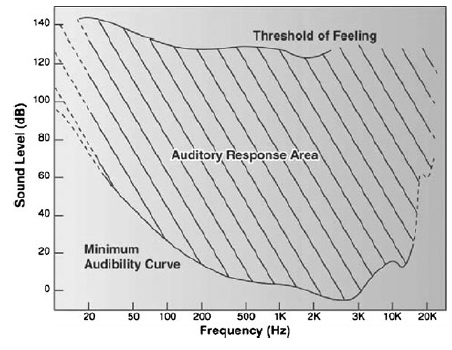
สาเหตุที่เลือกใช้ย่านความถี่สูง เพราะหูคนเรานั้นไม่ค่อยอ่อนไหวต่อความถี่สูงเท่าไรนัก เมื่อเทียบกับย่านความถี่เสียงพูด (ดูรูปด้านล่าง) ผู้เขียนจึงเลือกที่จะดัดแปลง wavelet coefficient ของย่านความถี่แถว ๆ 10 kHz ในการฝังข้อมูล watermark bit และสาเหตุที่เลือกใช้ wavelet domain เพราะอาศัยข้อดีของ wavelet ที่เหนือกว่าการแปลงฟูริเยร์ อาทิ มันเป็น time-frequency analysis และเหมาะกับ non-stationary signal ทั้งยังมี computational complexity ต่ำกว่า จึงคำนวณเร็วกว่า และข้อดีอีกประการ (อาจจะด้วยความบังเอิญ) คือ การแยกย่านความถี่ด้วย wavelet นั้นล้อกับโครงสร้าง critical band ในระบบการรับรู้เสียงของมนุษย์ (เกี่ยวกับเรื่องนี้ ผมจะพูดถึงในบล็อกตอนอื่นอีกที)
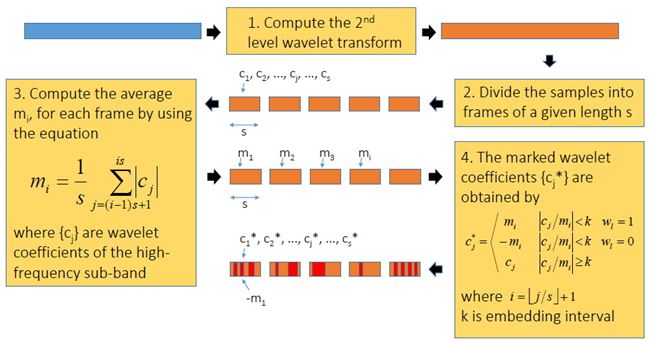
ขั้นตอนการฝังข้อมูลสรุปได้ดังแผนภาพด้านล่าง เริ่มจาก เราแปลง wavelet กับเสียง (สีฟ้า) ให้กลายเป็นสีส้ม ใช้เฉพาะย่านความถี่สูงนะครับ ต่อมาแบ่งออกเป็นท่อน ๆ ท่อนละ s แซมเปิ้ล แต่ละแซมเปิ้ลก็มี wavelet coefficient cj ของมัน เรากำลังจะดัดแปลงค่า cj ตัวนี้แหละเพื่อซ่อนข้อมูล เราคำนวณค่าเฉลี่ย mi ของ ส.ป.ส. ของแต่ละท่อน (โดยการหาผลรวมของ ส.ป.ส. ในท่อนนั้นแล้วหารด้วย s) และค่า ส.ป.ส. ที่จะดัดแปลง c*j เราจะเปลี่ยนมันเป็น mi หรือ -mi เมื่ออัตราส่วนระหว่าง cj ต่อ mi อยู่ภายในช่วง -k ถึง k โดยที่ k เป็นพารามิเตอร์ตัวหนึ่ง เรียกว่า embedding interval (ช่วงการฝัง) แต่ถ้า cj/mi ไม่อยู่ในช่วงการฝัง เราก็จะไม่ฝัง นั่นคือ เราไม่ซ่อนข้อมูล ทีนี้ c*j จะเท่ากับ mi หรือ -mi ก็ขึ้นอยู่กับว่าข้อมูลที่จะฝังเป็น 1 หรือ 0 ตามลำดับ พูดอีกอย่างหนึ่งว่า ถ้า cj อยู่ในช่วง [-kmi, kmi] แล้ว c*j = mi เมื่อ watermark bit = 1 และ c*j = -mi เมื่อ watermark bit = 0 ตัวอย่างสีแดงในรูป คือ ช่วงที่มีการฝัง หลังจากดัดแปลง ส.ป.ส. เรียบร้อยแล้วก็ใช้ inverse DWT เพื่อสร้าง watermarked audio signal
สังเกตว่า ถ้า k มาก โอกาสที่ cj จะมีค่าอยู่ในช่วง [-kmi, kmi] ก็ยิ่งมาก ผลที่ตามมาคือ capacity และ distortion ก็มากตามด้วย capacity มากนี่ดี แต่ distortion มากนี่หมายถึงคุณภาพเสียงห่วย ฉะนั้นจะต้องมีการเลือกค่า k ที่เหมาะสมครับ
รูปด้านล่างแสดง wavelet samples ในระหว่างขั้นตอนการฝังข้อมูล a คือก่อนฝัง และ c คือหลังจากฝังแล้ว
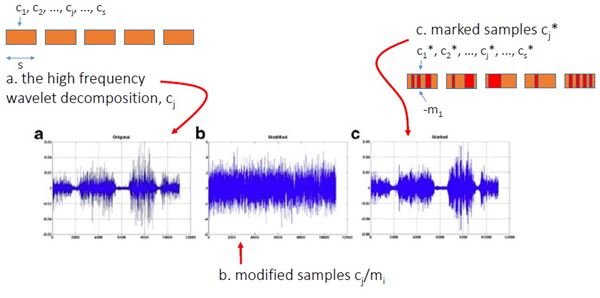
ผู้เขียนบอกว่า ในการดัดแปลงค่า c*j นั้น เขาไม่ดัดแปลงเป็น + หรือ - mi ตรง ๆ แต่ใช้ scale factor α ด้วย เพื่อควบคุมสมบัติด้าน robustness กับ transparency โดยค่าของ α อยู่ในช่วง (0.5,k) นั่นคือ c*j จะถูกเปลี่ยนเป็น + หรือ - αmi และ α ก็เป็นพารามิเตอร์อีกตัวที่ต้องเลือกอย่างชาญฉลาดเช่นกัน
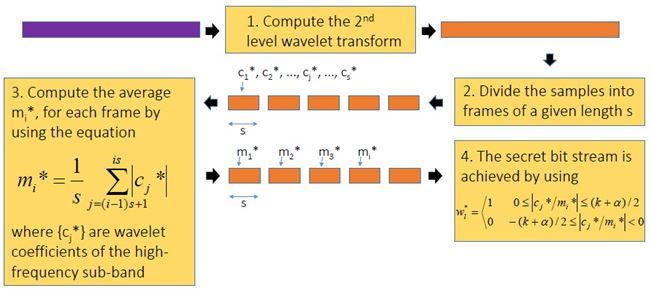
ขั้นตอนการดึงข้อมูลแสดงดังแผนภาพด้านล่าง เราทำเหมือนตอนฝังนะครับจนถึงขั้นคำนวณ m*i (สัญลักษณ์ superscript * ในที่นี้หมายถึง เป็นค่าของ watermarked audio signal) และเราก็ใช้แค่พารามิเตอร์ของระบบกับ m*i และ c*j ในการคำนวณ watermark bit (w*l) ตามสมการในขั้นตอนที่ 4 ตัวอย่างเช่น ถ้าพารามิเตอร์ของระบบ k = 2, α = 1 เมื่อเราหา c*j แล้วพบว่ามันอยู่ในช่วง [0, 1.5m*i] เราก็จะรู้ว่า w*l = 1 แต่ถ้า c*j อยู่ในช่วง [-1.5m*i, 0) ค่า w*l = 0
เห็นว่าพารามิเตอร์ที่ใช้ในระบบมีหลายตัว และการเลือกค่าพารามิเตอร์ก็ขึ้นอยู่กับความต้องการต่าง ๆ ของระบบ เช่น capacity, ODG, BER ที่เราอยากได้ ผู้เขียนได้เสนอขั้นตอนการปรับเลือกค่าพารามิเตอร์ดัง flowchar
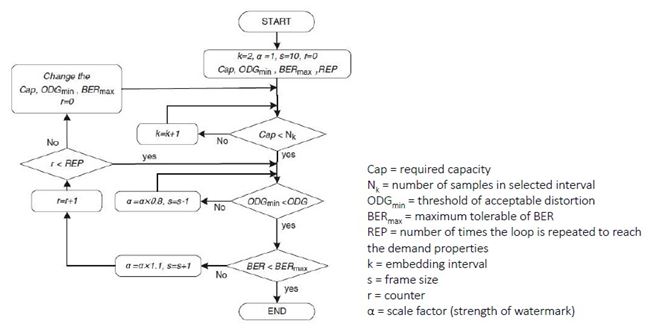
เช่น ถ้า ODG ต่ำกว่า ODGmin หมายถึง คุณภาพเสียงแย่ เราก็ควรปรับลด scale factor (ตาม flowchart การคูณ 0.8 คือ ปรับลดลง 20%) และลดขนาดของท่อน (เท่ากับเพิ่มจำนวนท่อน)
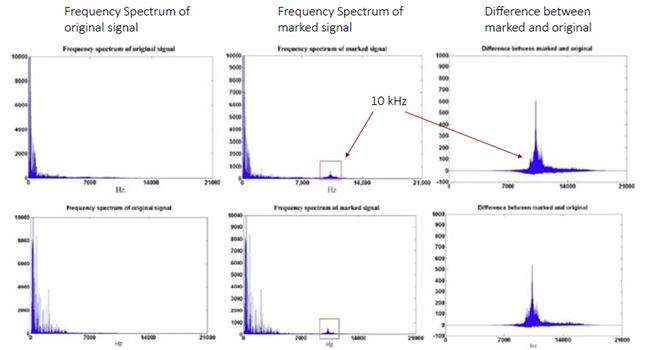
การทดลองในบทความใช้เพลง 5 เพลง (44.1 kHz, 16 bits/sample) โดยมีพารามิเตอร์ของระบบ k = 6, α = 2 และ s = 10 และเลือกใช้ Daubechies wavelet รูปด้านล่างแสดงสเปกตรัมความถี่ของเพลงสองเพลง (แถวละเพลง) โดยคอลัมน์แรกเป็นสเปกตรัมของเพลงต้นฉบับ คอลัมน์กลางเป็นสเปกตรัมของเพลงหลังจากฝังข้อมูล watermark แล้ว และคอลัมน์สุดท้ายเป็นผลต่างของสองคอลัมน์แรก (สเกลแนวแกน y คนละสเกลกันนะครับ, ภาพในบทความต้นฉบับที่ผมมีก็ไม่ค่อยชัดอย่างนี้แหละ) จะเห็นว่าส่วนที่แตกต่างอยู่ในย่านความถี่สูง 10 kHz
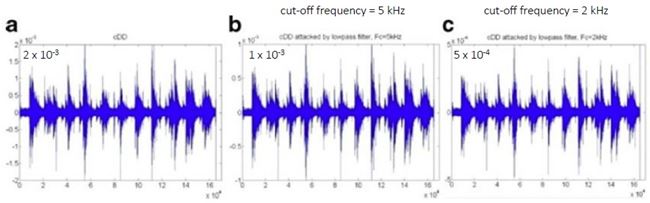
จุดขายอันหนึ่งที่ผู้เขียนบทความนี้ภูมิใจนำเสนอคือ ถึงแม้เราจะเห็นว่าข้อมูลไปซ่อนกันอยู่แถวย่านความถี่สูง 10 kHz (รูปบน) แต่ข้อมูลที่ซ่อนก็รอดจากการถูกโจมตีด้วย RC low-pass filter !!! รูปด้านล่างแสดง high frequency wavelet decomposition ของสัญญาณก่อนถูกโจมตี มี watermark ซ่อนอยู่แล้วนะ (a) และสัญญาณหลังจากผ่านการโจมตีด้วย LPF ที่มีความถี่ cut-off เท่ากับ 5 kHz และ 2 kHz (รูป b และ c ตามลำดับ) สังเกตว่ารูปทรงของสัญญาณเหมือนเดิม เปลี่ยนไปแค่สเกล และสเกลที่เปลี่ยนไปนั้นไม่มีผลกระทบต่อการดึงข้อมูลออกมา เพราะว่าเราใช้อัตราส่วนของ ส.ป.ส. ต่อค่าเฉลี่ยของ ส.ป.ส. ในการฝังข้อมูล
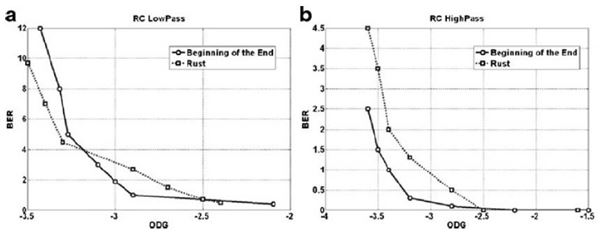
รูปต่อมาแสดง transparency กับ BER โดยใช้ ODG เป็นตัวระบุ transparency หรือคุณภาพของเสียงของเพลงสองเพลง (Beginning of the End กับ Rust) เมื่อถูกโจมตีด้วย (a) LPF กับ (b) HPF ตามลำดับ ข้อสังเกตประการหนึ่งคือ คุณจะเห็นว่าที่ BER สูง ๆ ODG จะต่ำกว่า -3 หมายความว่า LPF กับ HPF อาจทำลายข้อมูลที่ซ่อนในเพลงได้นะ (เพราะ BER สูง) แต่การทำลายนั้นจะต้องแลกกับ ODG ต่ำ (คุณภาพแย่) มันก็เปรียบเทียบได้กับ ผมมีกระดาษที่มีลายน้ำบนหน้ากระดาษ แล้วคุณบอกว่าคุณสามารถทำลายลายน้ำได้โดยการเอากระดาษไปเผาไฟ แน่นอนว่าลายน้ำถูกทำลาย แต่กระดาษก็ถูกทำลายไปด้วย ฉะนั้นมันจึงไม่เป็นประเด็นที่ผู้เขียนจะต้องกังวลครับ
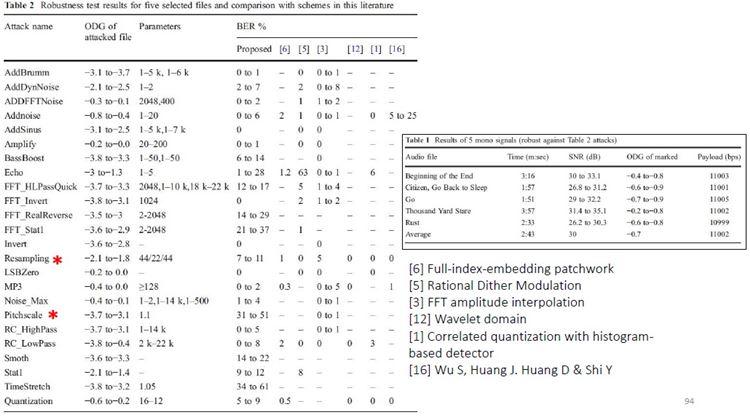
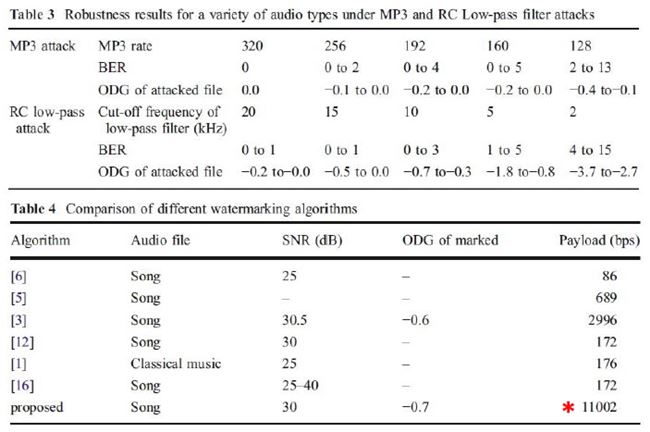
สำหรับตารางด้านล่าง ตารางที่ 1 แสดงค่าเฉลี่ยของเพลง 5 เพลงที่ถูกโจมตีโดยวิธีการในตารางที่ 2 และตารางที่ 2 ยังได้เปรียบเทียบการโจมตีนั้น ๆ กับวิธีการอื่น ๆ ดอกจันสีแดงที่ผมทำเอาไว้ ให้ดูเป็นจุดสังเกตว่าวิธีที่ผู้เขียนเสนอ แพ้ทาง resampling กับ pitchscale ตารางที่ 3 ตรง ๆ ตัว ดูเอง ตารางที่ 4 จะโชว์ว่าวิธีนี้รองรับ payload ขนาดมหึมาได้ชนิดแซงหน้าวิธีอื่นขาดลอย
| Create Date : 17 เมษายน 2556 | | |
| Last Update : 18 เมษายน 2556 0:03:44 น. |
| Counter : 2150 Pageviews. |
| |
|
 |
|
|
|
Judgment of Perceptual Synchrony Between Two Pulses and Its Relation to the Cochlear Delays
เนื้อหาตอนนี้ ส่วนที่เกี่ยวข้องกับการทดลองสรุปจากบทความชื่อเดียวกันของ Eriko Aiba, Minoru Tsuzaki, Satomi Tanaka และ Masashi Unoki ตีพิมพ์ใน J. Psychological Research Vol 50 No 4 ปี 2008 ผลลัพธ์ที่ได้จากการทดลองในบทความนี้ จะถูกนำไปใช้เป็นองค์ความรู้สำคัญในเทคนิค watermarking ที่อาศัยสมบัติ cochlear delay ซึ่งเสนอโดยอาจารย์ Unoki
คำสำคัญที่ควรนำมาขยายความก่อน คือ cochlear delay คืออะไร? ดูรูปส่วนประกอบของหูด้านล่างนะ
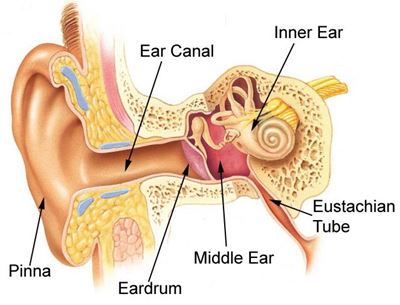
เริ่มจากส่วนนอกสุดคือใบหู อันที่จริงใบหูนั้นทำให้สเปกตรัมของสัญญาณเสียงเปลี่ยนแปลงเมื่อมันเดินทางผ่านเข้าไปในรูหู และการเปลี่ยนสเปกตรัมนี้ขึ้นอยู่กับทิศทางของเสียงที่เข้ามา ฉะนั้น ใบหูมีส่วนช่วยในการระบุตำแหน่งของแหล่งกำเนิดเสียงด้วยนะครับ ส่วนที่เป็น ear canal โดยฟังก์ชั่นจะทำหน้าที่เหมือนกับ band-pass filter มันทำให้คนเราอ่อนไหว (sensitive) หรือสามารถรับรู้ต่อความถี่ย่านเสียงพูดได้ดี จนถึงจุดนี้อากาศยังเป็นตัวนำพาเสียง และมาสิ้นสุดเอาที่ eardrum ความดันอากาศที่มากระทบ eardrum จะทำให้มันสั่น และมันเป็นอวัยวะที่อ่อนไหวและน่าทึ่งที่สุดในร่างกายมนุษย์ก็ว่าได้ เพราะเราสามารถตรวจจับการกระจัดของการสั่นได้ในระดับที่น้อยกว่า 1/10 ของขนาดอะตอมไฮโดรเจน (นั่นคือที่ความถี่ 1 kHz ของสัญญาณความถี่เดียว หรือ pure tone) หลังจากนั้นเสียงจะเดินทางเข้าสู่หูชั้นกลาง มีกระดูก 3 ชิ้น สัญญาณเสียงก็ส่งผ่านกระดูก 3 ชิ้นนี้แหละครับ ไม่ได้อาศัยอากาศอีกแล้ว ถึงแม้ว่าในหูชั้นนี้จะเต็มไปด้วยอากาศ เห็นท่อ eustachian มั้ย ท่อนั้นจะต่อกับด้านหลังของลำคอ อากาศที่เข้าออกผ่านท่อ eustachian จะปรับความดันภายนอกและภายในหูให้เท่ากัน (การเคี้ยวหมากฝั่งช่วยแก้หูอื้อขณะเครื่องบินกำลังบินขึ้นได้ก็ด้วยการปรับความดันอากาศของหูชั้นกลางผ่านท่ออันนี้) การเดินทางในตัวกลางที่เป็นกระดูกของเสียงก็สิ้นสุดลงตรงหูชั้นกลาง ที่หูชั้นในมันจะเดินทางต่อโดยอาศัยของเหลวที่อยู่ในอวัยวะรูปก้นหอย อวัยวะส่วนนั้นล่ะคือ cochlea จะเห็นว่าฟังก์ชั่นของหูชั้นกลางก็เหมือนกับเป็นตัวกลางระหว่างสองตัวกลางการเคลื่อนที่ของเสียง ฉะนั้น เราพูดได้ว่าเจ้ากระดูกสามชิ้นของหูชั้นกลาง คือ impedance-matching transformer รายละเอียดเกี่ยวกับ cochlea ผมจะเขียนถึงอีกทีในบล็อกตอนหลัง ๆ สำหรับตอนนี้ จะขอพูดตรงเข้าไปที่อวัยวะสำคัญซึ่งอยู่ภายใน cochlea คือ basilar membrane และความรู้เกี่ยวกับมันที่จำเป็นเพื่อให้เข้าใจบทความนี้ คือ เมื่อเสียงเดินทางผ่านของเหลว ตำแหน่งต่าง ๆ บน basilar membrane จะถูกกระตุ้นให้มีการสั่น โดยตำแหน่งที่สั่นจะขึ้นอยู่กับองค์ประกอบทางความถี่ของคลื่นเสียงนั้น โดยตำแหน่งที่ตอบสนองต่อความถี่สูงจะอยู่ส่วนต้น ๆ ติดกับหน้าต่างวงรี (ดูรปด้านล่าง) และตำแหน่งที่ตอบสนองต่อความถี่ต่ำลงค่อยเลื่อนไปทางปลายของ basilar membrane หมายความว่า ส่วนที่ติดกับหน้าต่างวงรีจะสั่นตอบสนองต่อความถี่สูง ขณะส่วนที่อยู่ปลายสุดจะสั่นตอบสนององค์ประกอบความถี่ต่ำสุด แต่ธรรมชาติไม่ได้ทำให้มันสั่นพร้อม ๆ กัน ถึงแม้ว่าคลื่นเสียงจะเดินทางจากหน้าต่างวงรีจนถึงปลายสุด (แล้วเดินทางอ้อมกลับไปออกทางหน้าต่างวงกลม) แทบจะพร้อม ๆ กัน (เสียงเดินทางในของเหลว) แต่ตำแหน่งที่ความถี่ที่ต่ำกว่าจะถูกกระตุ้นให้ basilar membrane ตอบสนองช้ากว่า นั่นทำให้เรามองเห็นการสั่นของ basilar membrane เสมือนเดินทางเป็นคลื่นจากหน้าต่างวงรีไปยังส่วนปลายของ membrane ลักษณาการที่ basilar membrane ใน cochlea ตอบสนองต่อองค์ประกอบความถี่ต่ำช้ากว่านี่แหละครับ คือ cochlear delays และการสั่นดังกล่าวนี้จะไปกระตุ้นเซลล์ประสาทซึ่งอยู่บน membrane (การสั่นจะดึงหรือกด ส่วนที่เราเรียกว่า tip links บนเซลล์ประสาทให้เปิดหรือปิดช่องที่ K+ ผ่าน) และสร้างสัญญาณไฟฟ้าส่งต่อไปตีความยังสมอง ฉะนั้น เราอาจมอง basilar membrane ว่ามันทำหน้าที่แปลงความถี่ไปเป็นตำแหน่ง (frequency-to-place transform)
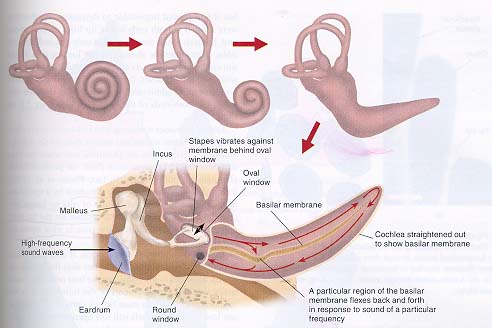
สรุปอีกทีนะครับ สมมติคุณเคาะโต๊ะหนึ่งทีในช่วงเวลาสั้น ๆ สัญญาณเสียงที่ได้ยินนั้นประกอบด้วยความถี่ที่แตกต่างกันมากมาย แต่ละความถี่เกิดขึ้นพร้อม ๆ ในทางกายภาพ แต่พอเสียงเคาะโต๊ะที่มีหลาย ๆ ความถี่อันนี้ไปถึง cochlea เจ้า basilar membrane จะมองเห็นความถี่สูงเกิดขึ้นก่อน มันจึงสั่นที่บริเวณใกล้หน้าต่างวงรีก่อน แล้วความถี่ต่ำกว่าค่อยเกิดขึ้นตามมาทีหลัง ในมุมมองของ basilar membrane มันจึงเห็นความถี่ที่แตกต่างกันมากมายเหล่านั้นเกิดขึ้นไม่พร้อมกัน
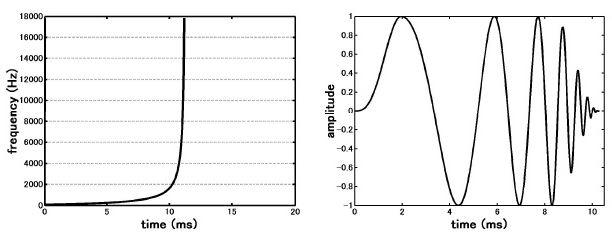
ทีนี้ ถ้าเราอยากทำให้ทุก ๆ องค์ประกอบความถี่ไปกระตุ้นให้ basilar membrane สั่นพร้อม ๆ กันล่ะ เราจะทำได้อย่างไร ไอเดียไม่ยากครับ ถ้าเรารู้ว่าแต่ละความถี่มีการหน่วงเวลาเท่าไร เราก็ชดเชยเวลาที่หน่วงไปนั้น พูดอีกอย่างหนึ่งว่า แทนที่เราจะป้อนสัญญาณซึ่งทุก ๆ ความถี่เกิดขึ้นทางกายภาพพร้อม ๆ กัน เราก็ปล่อยให้ความถี่ต่ำไปก่อนด้วยค่าระยะเวลาหนึ่งแล้วค่อยปล่อยความถี่สูงตาม เราจะได้สัญญาณดังรูป สัญญาณนี้เรียกว่าสัญญาณที่มีการชดเชยการหน่วงเวลา (compensatory delay)
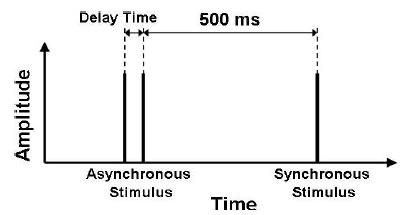
โอเค เราพร้อมที่จะดูการทดลองตามบทความแล้วล่ะครับ คณะนักวิจัยทำแบบนี้ ผู้ร่วมทดลองจะได้ยินเสียง 2 เสียง ทั้งสองเสียงนั้นถูกปล่อยโดยทิ้งช่วงเวลาห่างกันครึ่งวินาที (ดูรูปด้านล่าง) โดยในแต่ละเสียงนั้นจะประกอบด้วยสัญญาณที่เหมือนพัลซ์ 2 สัญญาณ ซึ่งในเสียงหนึ่ง สัญญาณทั้งสองจะเกิดขึ้นพร้อมกัน (synchronous) ในขณะที่อีกเสียงหนึ่ง สัญญาณทั้งสองจะเกิดขึ้นไม่พร้อมกัน (asynchronous) และมีช่วงเวลาระหว่างสัญญาณที่ไม่พร้อมกันเท่ากับ delay time ดูรูปด้านล่าง ตัวอย่างจากรูป เสียงแรกเป็น asynchronous เพราะมีสัญญาณคล้านพัลซ์ 2 สัญญาณเกิดขึ้นห่างกันเท่ากับ delay time แล้วอีกครึ่งวินาทีต่อมา เสียงที่สองเป็น synchronous เราเห็นขีดเพียงขีดเดียว เพราะสัญญาณคล้ายพัลซ์สองสัญญาณเกิดขึ้นพร้อมกัน หน้าที่ของผู้ร่วมทดลองคือให้บอกว่า เสียงไหน (เสียงแรกหรือเสียงที่สอง) เป็น synchronous และคำตอบที่ถูก หากผู้ร่วมทดลองฟังออกจากรูปตามตัวอย่างนี้ เขาจะตอบว่า เสียงที่สอง
ผมใช้คำว่าสัญญาณคล้ายพัลซ์ (pulse-like) เพราะ ผู้ทดลองมีการเลือกใช้สัญญาณ 3 แบบ คือ (1) สัญญาณพัลซ์ธรรมดา (intrinsic cochlear delay) แบบเดียวกับสัญญาณที่เกิดจากเสียงเราทุบโต๊ะสั้น ๆ หนึ่งทีนั่นแหละครับ องค์ประกอบทางความถี่ของเสียงทุกความถี่เกิดขึ้นพร้อม ๆ กันทางกายภาพ และมันก็จะไปดีเลย์องค์ประกอบความถี่ต่ำบน basilar membrane ตามธรรมชาติ (2) สัญญาณที่ชดเชยดีเลย์ (compensatory delay) ซึ่งก็คือสัญญาณที่เห็นในรูปด้านบน ปล่อยความถี่ต่ำออกมาก่อนแล้วตามมาด้วยความถี่สูง เพื่อให้ทุก ๆ ความถี่ไปกระตุ้น basilar membrane พร้อม ๆ กัน และ (3) สัญญาณที่ดีเลย์ความถี่ต่ำให้นานขึ้นไปอีก (enhanced delay) ก็คือปล่อยความถี่สูงก่อนแล้วค่อยปล่อยความถี่ต่ำตาม ปกติ ถ้ามันไปพร้อม ๆ กัน ความถี่ต่ำก็ถูกดีเลย์ตามธรรมชาติอยู่แล้วใช่มั้ยครับ แต่อันนี้แกล้งปล่อยให้มันไปช้า มันก็ยิ่งดีเลย์ขึ้นไปอีก แน่นอนว่าผู้ร่วมการทดลองไม่รู้ว่าตนกำลังฟังเสียงที่ประกอบจากสัญญาณแบบไหนในสามแบบนี้
พารามิเตอร์ delay time ที่ใช้ในการทดลองมี 0.2 0.3 0.5 0.8 1.3 2.0 และ 3.2 ms ถ้าเราใช้ common sense เราก็บอกได้ว่ายิ่ง delay time มาก คนฟังก็ยิ่งบอกได้ง่ายว่าเสียงไหน sync เสียงไหนไม่ sync และผลการทดลองก็สอดคล้องกับ common sense นั่นแหละ ผู้เขียนบอกว่า อัตราส่วนของคำตอบที่ถูกเพิ่มขึ้น เมื่อ delay time เพิ่มขึ้น
ผลลัพธ์จากการทดลองที่สำคัญคือ เขาพบว่า สัญญาณชนิด compensatory delay จะทำให้เราตัดสินว่าเสียงไหน sync ยากขึ้น ขณะที่สัญญาณชนิด enhanced delay จะให้ผลการตัดสินใจใกล้เคียงกับสัญญาณพัลซ์ธรรมดา (intrinsic cochlear delay) หรือพูดอีกอย่างหนึ่งว่า เราแยกเสียง enhanced delay กับ intrinsic cochlear delay ไม่ค่อยออกหรอก นี่คือไอเดียหลักที่ใช้ในเทคนิคลายน้ำเสียงของอาจารย์ Unoki ที่ได้เสนอและตีพิมพ์ในปีต่อมา
| Create Date : 16 เมษายน 2556 | | |
| Last Update : 17 เมษายน 2556 1:16:15 น. |
| Counter : 4729 Pageviews. |
| |
|
| |
|
|
|
A New Audio Watermarking Scheme Based on Singular Value Decomposition and Quantization
เนื้อหาตอนนี้สรุปจากบทความในชื่อเดียวกันของ Vivekananda Bhat K กับ Indranil Sengupta ตีพิมพ์ใน Circuits Systems and Signal Processing Vol 30 Issue 5 หน้า 915-927 ปี 2011 ผู้เขียนเสนออัลกอริทึมสำหรับ audio watermarking ที่ robust (หมายถึง ลายน้ำยังคงอยู่แม้สัญญาณเสียงจะถูกโจมตี ไม่ว่าโดยเจตนาหรือไม่เจตนา) และ blind (หมายถึง การดึงข้อมูล watermark ออกมาจากสัญญาณเสียงนั้น สามารถกระทำได้โดยไม่ต้องอาศัยสัญญาณเสียงต้นฉบับ) โดยใช้เทคนิค Singular Value Decomposition (SVD) กับ Quantization Index Modulation (QIM)
SVD เป็นการแยกตัวประกอบ (decomposition) ของเมตริกซ์ Hpxp ใด ๆ ให้อยู่ในรูปของผลคูณของเมตริกซ์ 3 ตัว Hpxp = UDVT ในบทความนี้ ผู้เขียนสร้างให้ H เป็นเมตริกซ์จัตุรัสขนาด pxp (แต่ตามทฤษฎีบทนั้น เมตริกซ์ที่เราจะนำมาแยกตัวประกอบไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัส) U กับ V เป็น orthogonal matrix (หมายความว่า UUT = UTU = I และ VVT = VTV = I หรือพูดอีกอย่างหนึ่งว่า UT = U-1 และ VT = V-1) โดยแต่ละคอลัมน์ของ U กับ V คือ eigenvector ของ HHT กับ HTH ตามลำดับ (หายังไง? ตัวอย่างขั้นตอนการหา 1. คำนวณ HHT 2. หา eigenvalue (λi) พร้อม eigenvector (U'i) ที่สัมพันธ์กับ eigenvalue นั้น กล่าวคือ เราหาค่า λi และ U'i ที่สอดคล้องกับสมการ (HHT)U'i = λiU'i 3. สร้างเมตริกซ์ U' จาก eigenvector U'i โดยเรียงลำดับเวกเตอร์ตามลำดับค่า λi จากมากไปน้อย (นั่นคือ เวกเตอร์สำหรับค่า λ มากที่สุดอยู่คอลัมน์แรก) 4. ดำเนินการตามขั้นตอน Gram-Schmidt orthonormalization กับแต่ละคอลัมน์ของ U' เพื่อเปลี่ยนเวกเตอร์แต่ละตัวให้เป็น orthonormal vector (ทุกเวกเตอร์มีขนาดเท่ากับ 1 และ orthogonal ซึ่งกันและกัน) ผลลัพธ์ที่ได้นี่แหละครับคือ U) สำหรับ D คือ diagonal matrix ที่ค่าตามแนวทแยงมุมหลักเท่ากับรากที่สองของ λi เรียงจากมากไปน้อย และไม่เท่ากับศูนย์ (D11 = λ ที่มีค่ามากที่สุด) ค่ารากที่สองของ eigenvalue ซึ่งเป็น element ของ D นี่แหละครับที่เราเรียกว่า Singular Value (SV)
ผู้เขียนบอกว่า SVD-based watermarking scheme ส่วนใหญ่นั้น ฝัง watermark bits ด้วยวิธีการดัดแปลงค่า SV, คำถาม ทำไมเลือกเปลี่ยนค่า SV? มันมีประโยชน์หรือข้อดีอย่างไร?
ผู้เขียนอ้างข้อดีของการจัดการกับค่า SV ไว้ดังนี้ (1) การเปลี่ยนค่า SV ไม่กระทบต่อคุณภาพของสัญญาณอย่างมีนัยสำคัญ (2) SV เป็นปริมาณที่ไม่ผันแปร (invariant) ภายใต้การดำเนินการประมวลผลสัญญาณทั่ว ๆ ไป ข้อนี้หมายความว่า หลังจากที่สัญญาณถูกดำเนินการบางอย่างแล้วนั้น ค่า SV จะยังคงเดิม (3) ขนาดของเมตริกซ์จากการแปลง SVD ไม่ตายตัว และเมตริกซ์ไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัส (4) สมบัติทางพีชคณิตของ SV และ (5) วิธีการนี้ง่าย ไม่ซับซ้อน และให้ผลลัพธ์ที่ดี
ลองมาดูขั้นตอนการฝังข้อมูลกัน จากรูปด้านล่าง เราจะฝัง watermark image (W) ขนาด M x M บิต W = {w(i,j), 1 ≤ i ≤ M, 1 ≤ j ≤ M} ซึ่งเป็น binary image หรือ w(i,j) ∈ {0,1} คือ pixel value ที่ตำแหน่ง (i,j)
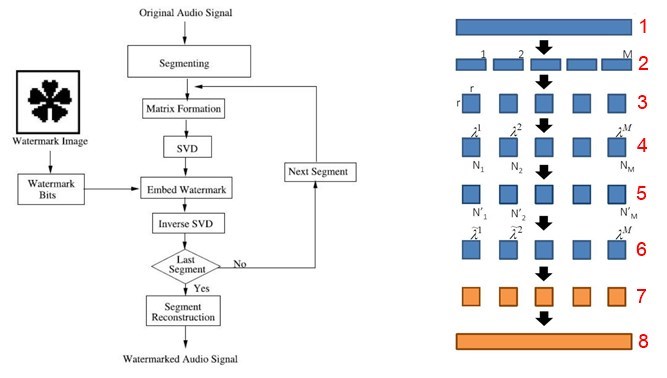
เริ่มต้นจาก ตัดสัญญาณเสียง A (เลข 1 สีแดง) ออกเป็นท่อน ๆ ท่อนละ r x r บิต (r เป็นพารามิเตอร์ตัวหนึ่งที่จะถูกปรับแต่งในการทดลองเพื่อ trade-off ระหว่าง imperceptibility, robustness กับ data payload) จำนวน M x M ท่อน (เลข 2 สีแดง, ตรงนี้ผมสร้างรูปผิดนิดหน่อยนะครับ ตัวอักษร M บนแท่งสีฟ้าขวามือสุด ที่ถูกจะต้องเป็น M x M แต่ขี้เกียจสร้างรูปใหม่ล่ะ เหตุผลที่ผู้เขียนแบ่ง A ออกเป็น M x M ท่อน ก็เพื่อจะฝังแต่ละท่อนด้วย watermark bit แต่ละบิตของ watermark image) จากนั้น นำแต่ละท่อนมีสร้างเป็นเมตริกซ์ (บล็อก 2-D) Bj (แสดงด้วยเลข 3 สีแดง) แล้วทำ SVD กับแต่ละ B เราก็จะได้ค่า SV ถ้ากำหนดให้ λj = (λj1, λj2, ..., λjr) เป็นเวกเตอร์ของ SV ของบล็อก Bj (สัญลักษณ์ λ ตั้งแต่ย่อหน้านี้เป็นต้นไป ไม่ใช่ตัวเดียวกับ λ ในย่อหน้าที่ 2 นะ ผมใช้ λ ในย่อหน้าที่ 2 แทน eigenvalue เพราะเป็นสัญลักษณ์สากลที่ใช้กันในทางคณิตศาสตร์ และใช้ λ แทน SV ในย่อหน้านี้เพราะผู้เขียนบทความใช้ λ = SV อย่าลืมว่า SV เป็นค่ารากที่สองของ eigenvalue นะครับ) เราใช้ λj ในการหา Euclidean norm ด้วยสมการ Nj = |λj| = √(∑(λji)2) เมื่อ i มีค่าตั้งแต่ 1 ถึง r
เราคำนวณ norm ของแต่ละบล็อก เพราะจะดัดแปลงค่าของมัน (ขั้นตอนการดัดแปลงค่านี้แหละครับคือ quantizing หรือพูดอย่างเจาะจง เทคนิคที่ใช้คือ QIM) โดยกำหนด Yj = Nj mod Δ เมื่อ Δ เป็นพารามิเตอร์อีกตัวที่จะถูกปรับแต่งในการทดลอง ชื่อเรียกของ Δ คือ quantization coefficient ทีนี้ค่าของ norm ดัดแปลง หรือ N'j นั้นจะขึ้นอยู่กับ watermark bit ถ้า watermark bit ที่เราจะฝังลงในบล็อกดังกล่าวคือ 1 และถ้า Yj < Δ/4 ค่า N'j = Nj - Δ/4 - Yj แต่ถ้า Yj ≥ Δ/4 ค่า N'j = Nj + 3Δ/4 - Yj กรณีที่ watermark bit คือ 0 และ Yj < 3Δ/4 ค่า N'j = Nj + Δ/4 - Yj แต่ถ้า Yj ≥ 3Δ/4 ค่า N'j = Nj + 5Δ/4 - Yj หลังจากผ่านขั้นตอนนี้ เราจะได้ norm ใหม่ของแต่ละบล็อก (เลข 5 สีแดง) ใช้ norm ใหม่, norm เก่า และเวกเตอร์ของ SV (λj) ของแต่ละบล็อก Bj ในการคำนวณเวกเตอร์ดัดแปลง (เขียนแทนด้วย λ*j) ของ SV ด้วยสมการ λ*j = λjN'j/Nj ขั้นตอนต่อมาใช้ λ*j คำนวณเมตริกซ์ดัดแปลง B*j โดยใช้ inverse SVD หรือ B*j = ∑λ*jiUi(j)VTi(j) เมื่อ i มีค่าตั้งแต่ 1 ถึง r ซึ่ง B*j ก็คือบล็อกข้อมูลเสียง (สีส้ม) ที่เราฝัง watermark bit ไปแล้วนั่นเอง
ขั้นตอนการดึง watermark image ออกมาจาก watermarked audio signal แสดงดังรูป
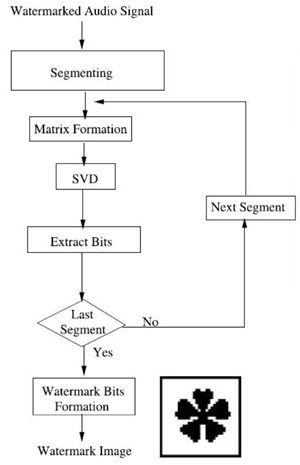
เริ่มต้นด้วยการนำ watermarked audio signal มาทำเป็นบล็อกขนาด r x r จำนวน M x M บล็อกเหมือนเดิม และแต่ละบล็อกก็ทำ SVD ทำนองเดียวกับขั้นตอนการฝัง คำนวณค่า norm ของแต่ละบล็อกออกมา จากนั้นเราสามารถบอกได้ว่า watermark bit ที่ฝังลงในบล็อกนั้นคืออะไรจากการดูว่า Yj < Δ/2 หรือไม่ เมื่อ Yj = Nj mod Δ ถ้า Yj < Δ/2 หมายความว่า watermark bit = 0 แต่ถ้า Yj ≥ Δ/2 เราก็จะรู้ว่า watermark bit = 1
บทความนี้ประเมินความสามารถของอัลกอริทึม 2 ด้าน คือ ด้านคุณภาพเสียง (imperceptibility) และด้านความทนทานต่อการถูกโจมตี (robustness) สำหรับ imperceptibility test นั้น ผู้เขียนได้ทดสอบทั้ง subjective และ objective test โดยใช้ subjective difference grade (SDG) กับ objective difference grade (ODG) เป็นตัวชี้วัดตามลำดับ ใน subjective test ผู้เข้าร่วมทดสอบจะได้ฟังไฟล์เพลง 8 เพลง (4 ประเภทเพลง ประเภทละ 2 เพลง) แต่ละเพลงจะได้ยิน 2 ครั้ง ครั้งหนึ่งเป็นไฟล์เสียงต้นฉบับ ส่วนอีกครั้งจะเป็นไฟล์เสียงหลังจากฝังข้อมูลลงไปแล้ว เขาจะต้องให้เกรด (SDG) 0 ถึง -4 เพื่อบอกว่าเขาสามารถรับรู้ถึงความแตกต่างระหว่างคุณภาพเสียงของไฟล์ทั้งสองของเพลงเดียวกันนั้นแค่ไหน โดยเกรด 0 คือ ไม่รู้สึกถึงความแตกต่างเลย (หมายความว่า คุณภาพเสียงหลังจากฝังลายน้ำดีมาก) และ -4 คือ แตกต่างกันจนถึงขั้นรับไม่ได้อย่างแรง (คุณภาพเสียงหลังจากฝังลายน้ำแล้วห่วยมาก) กรณี objective test ก็มีการให้เกรดเหมือนกับคนล่ะครับ เพียงเปลี่ยนจากคนตัดสินเป็นเครื่องจักรตัดสิน เครื่องจักรตัดสินตามมาตรฐาน PEAQ (perceptual evaluation of audio quality) ตามที่กำหนดไว้ใน ITU-R BS.1387

robustness test ใช้การคำนวณ NC (normalized correlation) กับ BER (bit error rate) เป็นตัวชี้วัด NC จะบอกว่า watermark image W กับ extracted watermark image W* เหมือนกันแค่ไหน ดูจากสมการข้างบน คงเห็นได้ไม่ยากว่าถ้า W* = W จะทำให้ NC = 1 นี่คือค่าที่เราต้องการ ส่วน BER บอกว่า W* กับ W มีจำนวนบิตที่แตกต่างกันกี่บิตเมื่อเทียบกับจำนวนบิตทั้งหมด ซึ่งก็คือ M x M วิธีเปรียบเทียบก็ทำตรงไปตรงมาด้วยการนับผลรวมของ w(i,j) xor w*(i,j) ถ้า W* = W ค่า BER = 0
สำหรับการทดลองในบทความนี้ ผู้เขียนเลือกใช้ r = 15 และ Δ = 0.59 พารามิเตอร์สองตัวนี้ถูกเลือกขึ้นมาเพื่อ trade-off ระหว่าง requirement ต่าง ๆ ของ watermarking ที่ขัดแย้งกันเอง พูดได้ว่า ค่า r กับ Δ ที่ผู้เขียนเลือกมานี้เป็นค่าที่ทำให้ SDG, ODG, NC สูงสุด ขณะที่ BER ต่ำสุด ผลลัพธ์ SDG กับ ODG แสดงดังตาราง
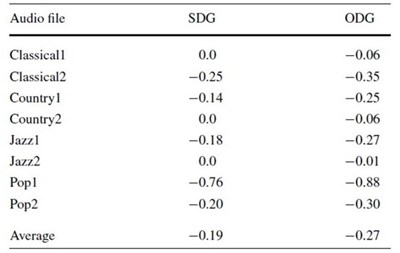
เห็นว่าเกรดใกล้เคียง 0 มาก แปลว่า คนและเครื่องจักรแยกความแตกต่างระหว่างคุณภาพของเสียงต้นฉบับกับเสียงที่ฝังข้อมูลลงไปแล้วแทบไม่ออก ตารางต่อมาแสดงผลลัพธ์เปรียบเทียบ watermark image ต้นฉบับกับ extracted watermark image ที่ดึงจาก watermarked audio signal หลังผ่านการโจมตีแบบต่าง ๆ ตัวเลขใต้ภาพแสดงค่า NC ซึ่งส่วนใหญ่ใกล้เคียงหนึ่ง นั่นหมายถึง robustness ของอัลกอริทึมที่ผู้เขียนเสนอ

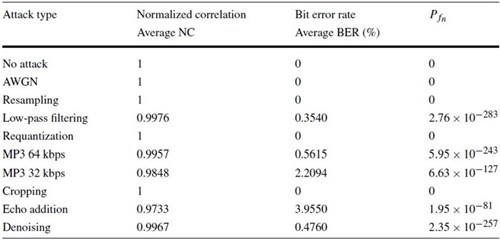
ตารางสุดท้าย แสดงค่า NC และ BER เมื่อถูกโจมตีด้วยการประมวลผลสัญญาณดิจิทัลแบบต่าง ๆ ในคอลัมน์สุดท้ายคือ Pfn หมายถึง โอกาสเกิด false negative error หรือ error ที่เกิดจากตัวถอดรหัสบอกว่า watermarked signal ไม่เป็น watermarked signal (นอกจาก false negative error ยังมี false positive error ที่ตัวถอดรหัสบอกว่า unwatermarked signal เป็น watermarked signal แต่เนื่องจาก Ppn ไม่เกี่ยวข้องกับโอกาสเกิด BER ผู้เขียนจึงไม่ให้ความสนใจ) ข้อมูลในตารางนี้แสดงให้เห็น robustness ได้เป็นอย่างดี
| Create Date : 14 เมษายน 2556 | | |
| Last Update : 14 เมษายน 2556 14:15:00 น. |
| Counter : 5487 Pageviews. |
| |
|
| |
|
|
|
|
|

