Pitch and Periodicity Coding [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 7 ในชื่อเดียวกัน หนังสือ The Sense of Hearing โดย Christopher J. Plack รายละเอียดบทที่ 2 - 6 ดูได้จากสารบัญกลุ่มเรื่องที่กำลังศึกษาตามลิงค์ข้างบนครับ ประเด็นของบทนี้ คือ ระบบการรับรู้เสียงสามารถนำเสนอและดึงข้อมูลเกี่ยวกับภาวะเป็นคาบ (periodicity) ของเสียงได้อย่างไร ซึ่งการรับรู้ภาวะเป็นคาบของเสียงนี่นะครับ จะสัมพันธ์กับปริมาณตัวหนึ่งที่เรียกว่า pitch ทำนองเดียวกับคู่ ความดัน-ความดัง ความดันเป็นปริมาณทางกายภาพที่สัมพันธ์กับความดังซึ่งเป็นปริมาณที่เรารับรู้ได้เมื่อเราได้ยินเสียง เป็น subjective และคู่ของ pitch ที่เป็นปริมาณทางกายภาพก็คือ ความถี่ Pitchตอนที่เราได้ยินเสียงซึ่งมีความถี่มูลฐาน (fundamental frequency) ค่าใดค่าหนึ่ง เราอาจจะรับรู้ถึง pitch ที่สัมพันธ์กับความถี่มูลฐานนั้น นั่นคือ ระบบจะต้องมีความสามารถในการระบุความถี่มูลฐานของเสียงนิยามของ pitch ที่ผู้เขียนใช้นะครับ pitch เป็นลักษณะของการรับรู้เสียงที่ความแตกต่างของมันสัมพันธ์กับทำนองเพลง พูดอีกอย่างหนึ่งว่า เสียงใดก็ตามที่ให้การรับรู้เกี่ยวกับ pitch (หรือ เสียงใดก็ตามที่เรารับรู้ pitch ได้) เสียงนั้น ก็สามารถนำไปใช้สร้างทำนองเพลงได้โดยเปลี่ยนอัตราการซ้ำคาบของเสียง แต่ถ้าเสียงไม่ทำให้เกิดการรับรู้ pitch เราก็เอาเสียงนั้นไปทำเป็นทำนองเพลงไม่ได้ เช่น คุณไม่สามารถใช้เสียงที่ความถี่สูงกว่า 5 kHz หรือต่ำกว่า 25 Hz ไปสร้างทำนองเพลงได้ ก็แปลว่า เสียงในช่วง 25 Hz ถึง 5 kHz เท่านั้นที่ทำให้เกิด pitch ส่วนเสียงที่มีความถี่อยู่นอกช่วงนี้ ไม่ทำให้เกิดการรับรู้ pitch รูปด้านล่างแสดง waveform กับสเปกตรัมของเสียง 3 เสียง เสียงแรก บนสุดเป็น pure tone เสียงที่สองกับสามเป็น complex tone ทั้งสามเสียงมี pitch เดียวกัน เพราะทั้งสามเสียงมีความถี่มูลฐานเดียวกัน (ความถี่มูลฐานเป็นตัวกำหนด pitch) ความถี่มูลฐานของ pure tone คือ ความถี่ของ pure tone สำหรับความถี่มูลฐานของ complex tone คืออัตราการซ้ำคาบของ waveform  คำถามต่อมา ความถี่สูงสุดและต่ำสุด (หรือความถี่มูลฐานสูงสุดและต่ำสุด) เท่าไรที่สามารถทำให้เกิด pitch ในกรณีของ pure tone มีการศึกษาของ Attneatve กับ Olson (1971) พบว่า ความถี่ที่สูงกว่า 4 kHz - 5 kHz ไม่สามารถนำมาสร้างทำนองเพลงได้ และนี่ก็เป็นค่าสูงสุดของความถี่มูลฐานของ complex tone ที่สามารถทำให้เกิด pitch ได้เช่นกันในกรณีที่มันมีฮาร์มอนิกแรกชัดเจน ซึ่งค่าดังกล่าวก็สอดคล้องกับโน้ตเสียงสูงสุด (เสียงแหลม) ที่วงออร์เคสตร้าสามารถเล่นได้ด้วย piccolo คือประมาณ 4.5 kHz และทำนองเพลงที่ใช้โน้ตความถี่สูงกว่านี้เล่นจะฟังประหลาด ๆ คุณสามารถบอกได้นะครับว่าเสียงมันเปลี่ยนแปลง แต่มันไม่เปลี่ยนแปลงในแบบที่ทำให้เป็นเพลง ถึงแม้ฮาร์มอนิกแรกของ complex tone ไม่มีในเสียง แต่เสียงนั้นก็สามารถทำให้เกิด pitch ได้ และช่วงของความถี่มูลฐานที่ทำให้เกิด pitch ขึ้นอยู่กับฮาร์มอนิกที่มีอยู่ในเสียง Ritsma (1962) แสดงให้เห็นว่า กรณีที่ความถี่มูลฐานเท่ากับ 100 Hz การใช้ complex tone ที่มีฮาร์มอนิกแค่ 3 ตัวต่อกัน ไม่สามารถทำให้เกิด pitch ได้เมื่อใช้ฮาร์มอนิกตัวที่สูงกว่าตัวที่ 25 แต่สำหรับเสียงที่มีความถี่มูลฐาน 500 Hz ขีดจำกัดบนจะอยู่ประมาณฮาร์มอนิกตัวที่ 10 ทางด้านความถี่ต่ำ พบว่า สำหรับ broadband complex tone ที่มีฮาร์มอนิกตั้งแต่ตัวแรกเป็นต้นไป สามารถนำไปเล่นทำนองเพลงได้ที่ความถี่มูลฐาน 30 Hz ซึ่งก็ใกล้เคียงกับโน้ตต้ำสุด (เสียงทุ้ม) ของเปียโน 27.5 Hz สรุป เสียงในช่วงความถี่ 30 - 5 kHz ทำให้เกิด pitch How Is Periodicity Represented?ในการตอบสนองต่อ pure tone นั้น firing rate ของนิวรอนขึ้นอยู่กับระดับของ pure tone ยิ่งระดับเสียงสูง firing rate ก็ยิ่งสูง (จนกว่าจะอิ่มตัว) และยังขึ้นอยู่กับความถี่ของ pure tone ยิ่งความถี่ใกล้กับความถี่ลักษณะเฉพาะของนิวรอน firing rate ก็ยิ่งสูง นั่นคือ firing rate ของนิวรอนในเส้นประสาทรับรู้เสียง เป็นตัวให้ข้อมูลเกี่ยวกับความถี่ของ pure tone และความถี่ลักษณะเฉพาะของนิวรอนตัวที่สร้าง spike มากสุด ก็ควรจะเท่ากับความถี่ของ tone (อย่างน้อยก็ที่ระดับเสียงต่ำ) นอกจากนี้ ความถี่ยังอาจถูกนำเสนอผ่านรูปแบบ (pattern) ของกิจกรรมของทุกนิวรอนที่มีความถี่ลักษณะเฉพาะแตกต่างกัน รูปต่อไปนี้แสดง excitation pattern ของนิวรอนชนิดเส้นใยมี spontaneous rate สูง ของ pure tone สองตัวที่มีความถี่ต่างกัน 10%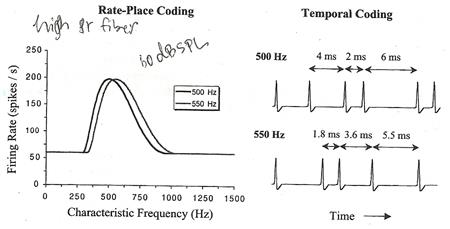 เห็นว่า ความแตกต่างระหว่างสองเสียงนี้ไม่ได้ถูกนำเสนอด้วยตำแหน่งจุดสูงสุดของ excitation pattern เท่านั้น แต่ firing rate ที่ความถี่ลักษณะเฉพาะใด ๆ ก็ต่างกันด้วย สำหรับภาพด้านขวาแสดงให้เห็นผลจากความโน้มเอียงของนิวรอนที่จะล็อคกับเฟสเฉพาะบางเฟสต่อการสั่นของ basilar membrane นั่นคือ ตอนที่ถูกกระตุ้นโดย pure tone นิวรอนจะผลิต spike ที่บางเฟสของ waveform ทำให้ ช่วงระหว่าง spike ประมาณเป็นจำนวนเต็มเท่าของคาบของ pure tone ฉะนั้น ความถี่ที่แตกต่างกัน ย่อมทำให้รูปแบบของ spike ในโดเมนเวลาแตกต่างกัน เช่น กรณี pure tone ความถี่ 500 Hz (คาบ = 1/500 = 2 ms) ระยะห่างระหว่าง spike มีแนวโน้มที่จะเท่ากับ 2, 4, 6, ... ms ส่วน pure tone 550 Hz (คาบ = 1.8 ms) ระยะห่างระหว่าง spike มีแนวโน้มที่จะเท่ากับ 1.8, 3.6, 5.5, ... ms (ดูรูปบนขวา) ซึ่งการล็อคเฟสนี้จะเกิดขึ้นกับนิวรอนที่ตอบสนองต่อโทนไม่ว่าจะเป็นนิวรอนตัวใดก็ตาม และถึงแม้มันจะอิ่มตัวแล้ว แต่เฟสก็ยังคงล็อคอยู่ ถึงตอนนี้เราก็พูดได้ว่า ความถี่ของ pure tone ถูกแสดงด้วย (1) รูปแบบของกิจกรรมของนิวรอนที่มีความถี่ลักษณะเฉพาะต่าง ๆ กันทั้งหมด และ (2) รูปแบบของกิจกรรมของนิวรอนในโดเมนความเวลา คำถามคือ ข้อมูลแบบ (1) หรือ (2) ที่สมองนำไปตีความเพื่อทำให้เกิดการรับรู้ pitch? ยังไม่มีคำตอบเอกฉันท์นะครับ แต่มีข้อเท็จจริงบางอย่างที่อาจช่วยในการหาคำตอบได้ หนึ่ง, ความสามารถในการแยกความถี่ของ pure tone สองตัวที่ความถี่ต่ำกว่า 4 kHz ของคนเรานั้น เราสามารถทำได้ดีมาก ประณีตมาก ละเอียดกว่าที่จะอธิบายได้ด้วยการเปลี่ยนแปลงของ excitation pattern รูปต่อไปนี้แสดงการแยกความถี่ของ pure tone (ที่มีความยาว 200 ms) ในโดเมนความถี่ เห็นว่า เราสามารถตรวจจับความแตกต่างระหว่าง pure tone ความถี่ 1000 Hz กับ 1002 Hz ได้  สอง, phase locking จะเริ่มล้มเหลวหรือไม่ล็อคที่ความถี่ 5 kHz ซึ่งมันช่างพ้องกันพอดีกับที่เราเริ่มไม่รับรู้ pitch ข้อเท็จจริงทั้งสอง ทำให้ผู้เขียนเชื่อว่า phase locking หรือ temporal coding หรือ ข้อ (2) เป็นส่วนจำเป็นสำหรับการรับรู้ pitch รูปด้านล่าง บน แสดงสเปกตรัมของ complex tone ซึ่งเป็นเสียง input, สเปกตรัมทั้งหมดของ input มีแอมปลิจูดเท่ากัน และเป็น complex tone ที่มีความถี่มูลฐานเท่ากับ 100 Hz, รูปกลาง แสดง excitation pattern และ รูปล่าง แสดงการจำลองการสั่นของ basilar membrane ที่ 5 ตำแหน่งที่มีความถี่ลักษณะเฉพาะต่างกัน (ชี้โดยลูกศร) และด้านขวามือของรูปล่างคือ waveform ของ complex tone  สังเกต ยิ่งความถี่สูง bandwidth ของฟิลเตอร์ก็ยิ่งกว้าง ดังนั้น มีเฉพาะฮาร์มอนิกต่ำ ๆ ไม่กี่ตัวแรกเท่านั้นที่ทำให้กราฟ excitation pattern มีลักษณะเป็นลูกคลื่นกระโดดแยกออกมา หมายความว่า เราสามารถได้ยินเสียงฮาร์มอนิกส์ 4-5 ตัวแรกนี้ของ complex tone แยกออกมาราวกับฮาร์มอนิกเหล่านั้นเป็น pure tone ได้ ส่วนที่ฮาร์มอนิกสูง ๆ หรือที่ความถี่กลางของฟิลเตอร์สูง ๆ นั้น excitation pattern ราบเรียบ (เพราะฟิลเตอร์ยอมให้ฮาร์มอนิกหลายตัวผ่านไปโดยไม่ลดทอนแอมปลิจูด เนื่องจาก bandwidth ของฟิลเตอร์กว้าง) นั่นคือ ฮาร์มอนิกสูง ๆ (สูงกว่าฮาร์มอนิกที่ 10) จะไม่ถูกแยกออกมา สรุปง่าย ๆ ว่า เมื่อดูจากการสั่นของ basilar membrane มันสามารถสั่นแยกฮาร์มอนิกต่ำได้ แต่แยกฮาร์มอนิกสูงไม่ได้ Plack กับ Oxenham (2005) บอกว่า cochlea สามารถแยกฮาร์มอนิก 8 ตัวแรกได้ โดยแทบไม่ขึ้นอยู่กับความถี่มูลฐาน แต่อย่างไรก็ตาม จำนวนของฮาร์มอนิกสูงสุดที่สามารถแยกได้จะลดลงที่ความถี่มูลฐานต่ำ (ต่ำกว่า 100 Hz) เนื่องจาก Q ของฟิลเตอร์มีค่าน้อยที่ความถี่กลางมีค่าต่ำ ข้อมูลเกี่ยวกับฮาร์มอนิกที่แยกออกมาแต่ละตัวจะถูกเก็บไว้ในเส้นประสาททั้งในรูปของ rate-place coding และ temporal coding ซึ่งข้อมูลเกี่ยวกับความถี่มูลฐานนั้น เราพึ่ง rate-place coding ไม่ได้มาก แต่ข้อมูลดังกล่าวมีอยู่ใน temporal coding จากการศึกษาของ Jorin กับ Yin (1992) พบว่า นิวรอนมีแนวโน้มที่จะล็อคเฟสกับ envelope ของการสั่นของ basilar membrane ดังนั้น ช่วงเวลาห่างระหว่าง spike จึงมีแนวโน้มที่จะเป็นจำนวนเต็มเท่าของของคาบของ complex tone เนื่องจาก คนเราสามารถแยกความแตกต่างของความถี่มูลฐานได้ดีมาก (ต่ำกว่า 1% สำหรับฮาร์มอนิกแยก เราก็ยังสามารถแยกความแตกต่างได้) จึงเชื่อกันว่า temporal coding เป็นตัวสำคัญในการส่งข้อมูลความถี่มูลฐาน  รูปนี้แสดงการสั่นของ basilar membrane กับรูปแบบ spike ในการตอบสนองต่อฮาร์มอนิกที่แยกออกมาตัวหนึ่ง (รูปซ้าย) กับฮาร์มอนิกหลาย ๆ ตัวที่ไม่แยกออกมา (รูปขวา) เห็นว่า เส้นใยประสาทที่จูนกับฮาร์มอนิกตัวที่แยก จะล็อกเฟสกับโครงสร้างละเอียด ขณะที่เส้นใยที่จูนกับฮาร์มอนิกที่ไม่แยก จะล็อคเฟสกับ envelope How Is Periodicity Extracted?คำถาม ระบบรับรู้เสียงนำข้อมูลในเส้นประสาทมาใช้อย่างไร ด้วยวิธีการใด เพื่อที่จะหา periodicity ของเสียง และทำให้เรารับรู้ pitch?เมื่อก่อน Ohm (1843) กับ Helmholtz (1863) คิดว่า pitch ของ complex tone ถูกกำหนดโดยความถี่ของฮาร์มอนิกแรก พวกเขาคิดว่า ถ้าเราได้ยินองค์ประกอบความถี่เสียงหลาย ๆ ตัว เราก็แค่ดึงความถี่ขององค์ประกอบต่ำสุดออกมา อันนั้นแหละคือความถี่มูลฐานและ periodicity ซึ่งในชีวิตประจำวันทั่ว ๆ ไป ไอเดียนี้ถูกต้องนะครับ ความถี่มูลฐานเท่ากับความถี่ของฮาร์มอนิกแรก แต่ในปี 1956 Licklider ได้แสดงให้เห็นว่า ถึงแม้เราจะเพิ่ม low-pass noise เพื่อทำการ mask ย่านความถี่บริเวณความถี่มูลฐานของ complex tone เราก็ยังคงได้รับรู้ pitch ได้เหมือนกับกรณีที่ไม่เติม noise ลงไป หมายความว่า ถึงแม้เราจะไม่ได้ยินองค์ประกอบมูลฐาน แต่ pitch ซึ่งสัมพันธ์กับ periodicity ของ complex tone ก็ไม่เปลี่ยนแปลง เท่ากับ ระบบรับรู้เสียงจะต้องสามารถดึงข้อมูลเกี่ยวกับความถี่มูลฐานจากฮาร์มอนิกที่สูงกว่าได้ ถึงแม้ฮาร์มอนิกแรกจะไม่จำเป็นต่อการรับรู้ pitch แต่ก็มีบริเวณหรือย่านฮาร์มอนิกลำดับต่ำ ๆ ที่สำคัญต่อการรับรู้ pitch ตัวอย่างจากการทดลองหนึ่งของ Moore, Glasberg กับ Peters (1985) ซึ่งได้เปลี่ยนความถี่ของฮาร์มอนิกตัวหนึ่งใน complex tone ดังรูป  เห็นว่า การเปลี่ยนความถี่ของฮาร์มอนิก ทำให้ pitch เปลี่ยน โดยตัวเลขขวามือของกราฟคือหมายเลขฮาร์มอนิกที่เปลี่ยนความถี่ (เพียงเล็กน้อย) ดังกล่าว Moore และคณะพบว่า การเปลี่ยนฮาร์มอนิกที่สอง สาม และสี่ ส่งผลกระทบต่อความถี่มูลฐานในช่วง 100 - 400 Hz มากที่สุด สำหรับอีกการทดลองหนึ่ง Dai (2000) พบว่า ฮาร์มอนิกส์ที่มีความถี่ราว ๆ 600 Hz เป็นตัวสำคัญสุด ซึ่งจะเป็นฮาร์มอนิกตัวที่เท่าไรนั้นขึ้นอยู่กับความถี่มูลฐาน เช่น ถ้าความถี่มูลฐาน 100 Hz ฮาร์มอนิกตัวที่หกเป็นตัวสำคัญที่สุด แต่ถ้าความถี่มูลฐาน 200 Hz ฮาร์มอนิกตัวที่สามก็สำคัญสุด ไม่ว่าหมายเลขที่แน่นอนของฮาร์มอนิกที่สำคัญต่อการรับรู้ pitch จะเป็นเท่าไร แต่สิ่งหนึ่งที่งานวิจัยทั้งหมดเห็นพ้องต้องกันคือ ฮาร์มอนิกที่แยกออกมา เป็นส่วนสำคัญที่สุดต่อการรับรู้ pitch หมายความว่า ถ้า complex tone ไม่มีฮาร์มอนิกที่สามารถแยกออกมาได้ ถึงแม้ complex tone ตัวนั้นอาจจะเอาไปสร้างทำนองเพลงได้ แต่มันจะให้ pitch ที่อ่อนมาก ไม่ชัดเจน นอกจากนี้ เรายังสามารถแยกความแตกต่างระหว่างความถี่มูลฐานของกลุ่มที่ประกอบด้วยฮาร์มอนิกแยก ได้ดีกว่าการแยกความแตกต่างระหว่างความถี่มูลฐานของกลุ่มที่ไม่มีฮาร์มอนิกแยก ดังรูป  จากรูป F0DL = fundamental frequency difference limen แกนตั้งเป็นความแตกต่างต่ำสุดในความถี่มูลฐานที่สามารถตรวจจับได้ โดยเสียงที่นำมาเปรียบเทียบแต่ละกลุ่มจะมีฮาร์มอนิก 11 ตัวต่อเนื่องกัน เห็นว่า ความสามารถในการตรวจจับความต่างแย่ลงตั้งแต่กลุ่มที่มีหมายเลขฮาร์มอนิกเท่ากับสิบเป็นฮาร์มอนิกต่ำสุดเป็นต้นไป คำถามต่อมา ระบบรับรู้เสียงใช้วิธีการใดในการหาความถี่มูลฐานของ complex tone? ตอนนี้มีโมเดลที่เสนอว่าอาจจะเป็นคำตอบอยู่ 2 โมเดล คือ pattern-recognition model กับ temporal model ไอเดียของ pattern recognition คือ ระบบรับรู้เสียงสามารถใช้ pattern ของความถี่ฮาร์มอนิกในการประมาณความถี่มูลฐาน เช่น ถ้ามีฮาร์มอนิกที่มีความถี่ 400, 600 กับ 800 Hz เราก็จะรู้ว่าเสียงดังกล่าวมีความถี่มูลฐาน 200 Hz หรือถ้ามีฮาร์มอนิก 750, 1250 กับ 1500 เราก็รู้ว่าความถี่มูลฐานเท่ากับ 250 Hz ทั้งนี้เพราะระยะห่างระหว่างฮาร์มอนิกที่ติดกันจะเท่ากับความถี่มูลฐาน ฉะนั้นใช้ฮาร์มอนิกต่ำ ๆ ที่แยกออกมาแค่สองตัวก็เพียงพอแล้วสำหรับการรับรู้ pitch ในการทำ pattern recognition ก็มีข้อเสนอว่าคงจะมี harmonic template ดังรูปด้านล่าง  สำหรับโมเดลนี้ อันดับแรก ระบบจะต้องแยกฮาร์มอนิกต่ำ ๆ ที่เป็นฮาร์มอนิกแยกออกมาก่อน แล้วดูว่าฮาร์มอนิกแยกเหล่านั้นเข้ากันกับ template อันไหนมากที่สุด ปัญหาของโมเดลนี้คือ มันไม่สามารถใช้อธิบายการรับรู้ pitch ของเสียงที่ไม่มีฮาร์มอนิกแยกได้ อีกโมเดลหนึ่ง temporal model หาความถี่มูลฐานจากการดูรูปแบบ spike ในเส้นประสาททั้งจากฮาร์มอนิกแยกและไม่แยก ดังรูป  รูปแสดงการสั่นของ basilar membrane และ phase locking ในเส้นประสาทที่ตอบสนองต่อฮาร์มอนิกที่หนึ่ง สอง สี่ หก และที่ความถี่ 1600 Hz (มีหลายฮาร์มอนิกไม่แยก) ไอเดียของโมเดลนี้คือ จะต้องมีระยะห่างระหว่าง spike สองตัวใด ๆ (เรียกว่า inter-spike interval) ในแต่ละเส้นใยที่สะท้อนถึงความถี่มูลฐานของเสียง (แสดงคาบด้วยลูกศร) และวิธีที่มีประสิทธิภาพในการหาคาบดังกล่าว เริ่มต้นด้วยการทำ autocorrelation หรือเปรียบเทียบสัญญาณใด ๆ กับสัญญาณหน่วงเวลา (ที่ค่าเวลาหน่วงต่าง ๆ กัน) ของตัวมันเอง ดังรูป  จะเห็นได้ว่า ที่เวลาหน่วงเท่ากับจำนวนเต็มเท่าของอัตราซ้ำคาบของ waveform นั้น correlation strength (หาจาก ผลรวมของผลคูณระหว่างสัญญาณต้นฉบับกับสัญญาณหน่วงเวลา ณ เวลาใด ๆ) จะมีค่าสูง หลังจากนั้น ให้เอาผลลัพธ์จาก autocorrelation แต่ละเส้น ทุกเส้น มารวมกันตรง ๆ เพื่อหาคาบร่วม ซึ่งคาบร่วมตัวนี้แหละครับเป็นส่วนกลับของความถี่มูลฐาน ข้อด้อยของโมเดลนี้คือ มันใช้อธิบายไม่ได้ว่า ทำไมเราสามารถแยกความแตกต่างของความถี่มูลฐานได้ดี และทำไม pitch ถึงมีความชัดเจนกว่าในเสียงที่มีฮาร์มอนิกแยกเมื่อเทียบกับเสียงที่ไม่มีฮาร์มอนิกแยก ข้อด้อยอีกประการมาจากการทดลองเอาพัลซ์บางตัวออกในแบบที่ไม่กระทบกับผลจาก autocorrelation ซึ่งหมายความว่า โมเดลนี้จะให้ความถี่มูลฐานเท่าเดิม ขัดกับผลการทดลองที่ผู้ฟังได้ยิน pitch ลดลง ข้อเสนอคือ เป็นไปได้ที่จะมีกลไกแยกต่างหากจากกันสำหรับฮาร์มอนิกแยกและฮาร์มอนิกไม่แยก โมเดล pattern recognition จึงยังมีโอกาสถูก แม้มันจะอธิบายเสียงที่ไม่มีฮาร์มอนิกแยกไม่ได้ นี่ยังเป็นเรื่องที่อยู่ในระหว่างการค้นคว้าครับ |
บทความทั้งหมด
|
 |





 ผู้ติดตามบล็อก : 85 คน [
ผู้ติดตามบล็อก : 85 คน [