Audio Watermarking Based on Spread Spectrum Communication Technique [สารบัญกลุ่มเรื่องที่กำลังศึกษา] เนื้อหาตอนนี้ผมสรุปจากบทที่ 7 How could music contain hidden information? หนังสือ Applied Signal Processing: A MATLABTM-Based Proof of Concept (Springer, 2009) เขียนโดย C. Baras, N. Moreau กับ T. Dutoit เราสามารถมอง watermarking ในสัญญาณเสียงเป็นเรื่องของปัญหาการส่งลำดับบิต 1 กับ 0 ผ่านช่องทางสื่อสารที่มี noise เยอะมากเป็นพิเศษได้ครับ โดยการมองแบบนี้ บิตที่เราจะส่งก็คือ watermark bit และ noise คือ สัญญาณเสียงนั่นเอง ฉะนั้น การทำ watermarking ก็เทียบเท่ากับการออกแบบตัวรับและตัวส่งที่สอดคล้องกับช่องทางพิเศษ รูปด้านล่างแสดงการมอง watermarking เป็นปัญหา communication ปัญหาหนึ่ง  สำหรับ watermarking เราต้องออกแบบ SNR ให้ต่ำมาก (SNR = Psignal/Pnoise) เพื่อให้หูคนไม่สามารถได้ยินข้อมูลที่จะฝังหรือซ่อน ผลสืบเนื่องจาก SNR ต่ำคือ bit rate ต่ำตาม (ดีที่สุดที่เป็นไปได้อยู่ที่หลักร้อยบิตต่อวินาที) และ error rate มีค่าสูง (ประมาณ 10-3 เมื่อเทียบกับระบบสื่อสารอย่าง ADSL ซึ่งอยู่ที่ 10-6) Spread Spectrum Signalsเริ่มแรก การสื่อสารด้วยเทคนิค Spread spectrum (SS) ใช้ในงานทางด้านการทหาร เพราะข้อเด่นของมันคือ 1. วิธีนี้ทนทาน (robust) ต่อการรบกวนในช่วงความถี่แคบ ๆ, 2. เป็นการส่งแบบแอบ ๆ ซ่อน ๆ และ 3. ความปลอดภัยในการส่งข้อมูลสัญญาณ SS มีลักษณะเฉพาะอยู่ 2 ประการ 1. bandwidth ของสัญญาณ SS ถูกทำให้กว้างกว่า bandwidth ของข้อมูลเดิมอย่างมาก (ทั่วไปประมาณ 10-100 เท่าสำหรับงานด้านพาณิชย์ และประมาณ 1,000 - 106 เท่า สำหรับงานการทหาร) การที่พลังงานมันแผ่กระจาย (spread) ในย่านที่กว้างนั้น ทำให้ PSD ต่ำลง ทำให้สัญญาณ SS มีโอกาสไปตีกับสัญญาณย่านความถี่แคบน้อยลง การสื่อสารย่านความถี่แคบแทบทำอะไรระบบ SS ไม่ได้เลย เพราะว่าตัวรับของระบบจะรวบรวมสัญญาณตลอดย่านที่กว้างมาก ๆ ในการดึงข้อมูลออกมา ข้อดีอีกประการจาก PSD ต่ำคือ เราสามารถทำให้มันต่ำกว่า PSD ของ noise ได้ อันนี้แหละครับคือลักษณะเด่นในการส่งข้อมูลแบบแอบ ๆ ซ่อน ๆ ของมัน 2. มีการใช้ spreading sequence (บางทีก็เรียก spreading code หรือ pseudo-noise) ในการสร้างสัญญาณ SS ย่านความถี่กว้างจากข้อมูลที่จะส่ง ซึ่งโค้ด spreading sequence นี้จะต้องเป็นที่รู้กัน รู้ตรงกัน ทั้งฝั่งส่งและฝั่งรับ ลักษณะ 2 อย่างนี้เป็นข้อดีใช่มั้ยครับ คำถาม ต้องเสียอะไรเป็นการแลกเปลี่ยนมั้ย? คำตอบ spectral efficiency หรือประสิทธิภาพของสเปกตรัมลดลง ประสิทธิภาพของสเปกตรัมนิยามจากอัตราส่วนระหว่างบิตเรตต่อ bandwidth ซึ่งเทคนิค SS จะให้ค่าที่ต่ำกว่า 1/5 ขณะที่เทคนิคมาตรฐานอื่น ๆ ให้ค่าเกือบ 1 Direct Sequence SS (DSSS)ใน DSSS หรือ time hopping นั้น สัญญาณ DSSS จะสร้างจากการคูณแต่ละคาบเวลาของหนึ่งบิต (bit-sized period หรือ Tb) ของสัญญาณที่จะส่ง (ในที่นี้สัญญาณที่จะส่งคือ watermark) ด้วย pseudo-noise ที่ประกอบจากลำดับลำดับอย่างสุ่มของพัลซ์สี่เหลี่ยม ±1 ซึ่งมีคาบเท่ากับ Tc ดังรูป รูปขวา บนสุดคือสัญญาณที่จะส่ง (watermark) มี Tb = 0.2 วินาที รูปกลางคือ pseudo-noise มี Tc = Tb/16 และรูปล่างคือสัญญาณ SS ที่ได้จากการคูณแต่ละคาบ Tb ของรูปบนด้วยรูปกลาง สำหรับรูปซ้าย แสดง PSD ของสัญญาณที่จะส่ง (หรือ รูปขวาบน) กับ PSD ของสัญญาณ SS เมื่อ Tc = Tb/4 และ Tb/16 ตามลำดับ เห็นว่า Tc ยิ่งต่ำ PSD ยิ่งต่ำ และที่ Tc = Tb/16 ต่ำกว่า PSD ของ noise เราคำนวณ PSD ของสัญญาณ SS ได้ไม่ยาก หากถือว่าสัญญาณที่จะส่งนั้นเป็นรหัสไบนารี่สุ่มแบบ NRZ ที่ประกอบจากพัลซ์สี่เหลี่ยมคาบ Tb และแอมปลิจูด ± 1/Tb เราจะได้ PSDNRZ(f) = [sinc2(fTb)]/Tb และเนื่องจากสัญญาณ SS เองก็เป็นสัญญาณ NRZ ที่พัลซ์มีคาบเท่ากับ Tc และแอมปลิจูด ± 1/Tb เราได้ PSDSS(f) = [Tcsinc2(fTc)]/Tb2 (ดังพล็อตในรูปซ้าย) Communication Channel Designเริ่มจากตัวส่ง (Emitter) โดยระบบสื่อสารแสดงดังรูปด้านล่าง สัญญาณเสียง x(n) ในที่นี้คือ noise ของระบบ มีอัตราสุ่มตัวอย่างเท่ากับ Fs Hz ถูกนำไปรวมเข้ากับ v(n) หรือสัญญาณ SS ของ watermark ที่สร้างมาจากการคูณ (หรือมอดูเลต) ลำดับของ watermark (bm ∈ {0,1}) ที่มีความยาวของลำดับเท่ากับ M บิต กับ pseudo-noise (หรือ spreading sequence, c(n)) ที่ประกอบด้วยตัวอย่างจำนวน Nb ตัว และเขียนแทนด้วยเวกเตอร์ c = [c(0), c(1), ..., c(Nb - 1)]T เจ้าเวกเตอร์ c นี้เราอาจสังเคราะห์ขึ้นมาจากตัวสร้างลำดับสุ่มเทียมที่มีค่าใน {-1, +1} อาทิ Walsh-Hadamard sequence หรือ Gold sequence เราไม่เอา bm มาใช้โดยตรง เพราะ bm ∈ {0, 1} เราก็แปลงมันเป็นสัญลักษณ์ชุดใหม่เรียกว่า am = 2bm - 1 ∈ {-1, +1} แล้วใช้คูณกับ c ก็จะได้ vm vm = amc หรือพูดว่า vm = +c ถ้า am = 1 (หรือ bm = 1) และ vm = -c ถ้า am = -1 (หรือ bm = 0) หลังจากนั้นจะเอา v(n) มาขยายด้วย gain g เพื่อควบคุม SNR ระหว่าง v(n) กับ x(n) จะเห็นว่า เราส่งข้อมูล (หรือฝังข้อมูล) 1 บิตทุก ๆ ตัวอย่าง Nb ตัว ดังนั้นบิตเรต R จึงคำนวณได้จาก Fs/Nb มาดูทางด้านฝั่งรับ (Receiver) บ้าง จากรูป เราได้ ym = gvm + xm หรือ ym = +gc + xm เมื่อ am = +1 และ ym = -gc + xm เมื่อ am = -1 โดย xm = [x(mNb, x(mNb+1), ..., x(mNb+Nb-1)]T เป็นเวกเตอร์ของตัวอย่างของ noise (หรือเสียง) ในช่องทางสื่อสาร และ m คือ frame index สำหรับบิตฝั่งรับหาได้จาก  (arg max = argument of the maximum, สัญลักษณ์ข้างบนหมายถึง ค่า b ที่ทำให้ P(b|ym) มีค่าสูงสุด) ในกรณีที่ช่องทางการสื่อสารเป็นช่องแบบ AWGN (additive white Gaussian noise) หรือช่องทางที่บวก white noise (หมายถึงสัญญาณสุ่มที่มี PSD คงที่) ซึ่งแอมปลิจูดของ noise มีการกระจายแบบปกติ (หรือ Gaussian distribution) ค่าดังกล่าวจะสมมูลกับการประมาณจากเครื่องหมายของผลคูณสเกล่า (αm) ระหว่าง ym กับ c  เพราะ เมื่อแทนที่ P(b|ym) ตามความสัมพันธ์ของเบส์ เราได้ 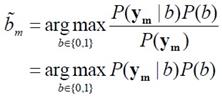 โดยที่ P(ym) เป็น priori probability ของ ym ซึ่งไม่มีผลกระทบต่อการประมาณค่า bm และ P(b) คือ priori probability ของแต่ละค่าที่เป็นไปได้ของ b และในกรณีที่ความเป็นไปได้นี้เท่ากัน มันก็จะไม่มีผลต่อการประมาณ bm ด้วยเช่นกัน ฉะนั้น  ในกรณีช่องทางสื่อสารแบบ AWGN นั้น xm เป็น ตัวแปรสุ่ม Gaussian แบบ Nb-dimensional multivariate ที่มีค่าเฉลี่ยเท่ากับ 0 และเมตริกซ์ความแปรปรวนร่วม (covariance matrix) เท่ากับ σx2I เมื่อ I คือเมตริกซ์เอกลักษณ์ Nb มิติ ทีนี้ ym ก็เป็นตัวแปรสุ่ม Gaussian ที่มี Nb ตัวแปรด้วย เพราะ ym = gvm + xm โดยมีค่าเฉลี่ยเท่ากับ amgc และเมตริกซ์ความแปรปรวนร่วมเดียวกับ xm จึงได้ 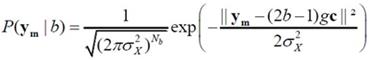 หรือ  เนื่องจาก b ∈ {0, 1} นั่นทำให้ (2b - 1)2 = 1 ไม่ว่า b จะมีค่าเท่าไร บรรทัดสุดท้ายของสมการนี้จึงบอกว่า เราสามารถหา bm ได้จาก เครื่องหมายของผลคูณเชิงสเกล่า αm ระหว่าง ym กับ c  รูปต่อไปนี้แสดงภาพกรณีฝัง bm = 1 ลงในเวกเตอร์เสียง x ได้เวกเตอร์หลังจากฝังแล้ว y ซึ่งคำนวณจาก gv + x หรือ gc + x เพราะ bm = 1 และทางฝั่งรับจะตีความว่า "1" ถ้า α > 0 รูปซ้ายแสดงกรณี <x,c> เป็นบวก และไม่ว่า g จะเป็นค่าบวกเท่าไรก็ตาม ย่อมทำให้ α > 0 ฉะนั้น bm = 1 นั่นคือดึงหรือรับข้อมูลได้ตรงกับที่ฝังหรือส่ง สำหรับรูปขวา เป็นกรณีที่ bm = 0 เนื่องจาก <x,c> เป็นค่าลบ และ g น้อยเกินไป กรณีนี้ดึงหรือรับข้อมูลได้ผิดนะครับ ถ้าอยากให้รับได้ถูก ต้องหาทางทำให้ g > <x,c>/|c|2 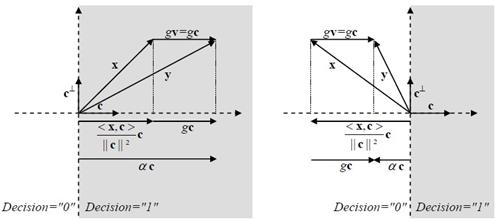 Error RatePDF ของ αm ที่ g = 1 และ σx2 = 20 dB แสดงดังรูป เมื่อค่า R เท่ากับ 50, 100 และ 120 ตามลำดับ (R = Fs/Nb โดยทั่วไป Fs เป็นค่าคงที่ 44.1 kHz ฉะนั้น อาจพูดว่า กราฟนี้พล็อตที่ความยาว Nb ต่าง ๆ กัน) รูปซ้ายคือกรณี b = 0 รูปขวา b = 1 αm เป็นตัวแปรสุ่ม Gaussian มิติเดียว ที่มีค่าเฉลี่ย (2bm - 1)g และความแปรปรวน σx2/|c|2  จะเห็นได้ว่า ความน่าจะเป็นที่ αm เป็นบวกเมื่อ bm = 0 และความน่าจะเป็นที่ αm เป็นลบเมื่อ bm = 1 ไม่เท่ากับศูนย์ (หมายความว่า มันมีโอกาสที่จะรับหรือดึงบิตออกมาได้ผิดค่า) และเมื่อค่า R มากขึ้น (กราฟ PDF เตี้ยลง และกระจายกว้างขึ้น) ความน่าจะเป็นดังกล่าวทั้ง 2 กรณีก็เพิ่มมากขึ้นตาม ความน่าจะเป็นที่จะอ่านค่าได้ผิดพลาดนี้หาได้จาก 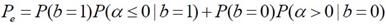 ถ้าสัญลักษณ์แต่ละตัวมี priori probability เดียวกัน (นั่นคือ P(b=1) = P(b=0)) ความน่าจะเป็นของ error สามารถประมาณโดยใช้กราฟด้านบน มีค่าเท่ากับ พื้นที่ซ้อนทับกันของ P(αm|bm = 0) และ P(αm|bm = 1) ซึ่งเราจะคำนวณ Pe ได้
ในสมการนี้เราใช้ σc2 = |c|2/Nb = กำลังของ pseudo-noise หรือ spreading sequence โดยประมาณ เห็นว่า ความน่าจะเป็นที่จะอ่านค่าผิดขึ้นอยู่กับ SNR ของ watermarking (= g2σc2/σx2) กับ R รูปด้านล่างแสดงกราฟ ซ้าย พล็อต Q(√u) กับ u ขวาพล็อต Pe(R) กับ R ที่ค่า SNR ต่าง ๆ กัน เมื่อ Fs = 44.1 kHz  Informed Watermarkingในระบบสื่อสารทั่วไปเราไม่รู้ noise ของช่องทางสื่อสารล่วงหน้า จึงเอามามันมาใช้ประโยชน์ในการปรับ gain ตอนเข้ารหัสไม่ได้ แต่สำหรับ watermarking นั้น เป็นไปได้ครับ เพราะ noise ในที่นี้คือเสียงที่เราจะใช้ซ่อนข้อมูลเราจะเริ่มด้วยการดูวิธีตรงไปตรงมาอย่างการปรับ gain เพื่อให้ตรวจรับข้อมูลได้อย่างไม่มีข้อผิดพลาด นั่นคือ ทางฝั่งส่งหรือฝั่งเข้ารหัสจะต้องมีการปรับค่า g ซึ่งเป็นฟังก์ชั่นของเวลาเพื่อชดเชยความผันผวนของกำลังแบบทันทีทันใดในสัญญาณเสียง และรักษา SNR ให้คงที่ ซึ่งทำได้ง่าย ๆ โดยการประมาณค่า σx2 ของเฟรมเสียง (~ 20 ms) แล้วกำหนดค่า g ให้แปรตาม σx ถ้าย้อนกลับไปดูกราฟ PDF ของ α เห็นว่า เราทำให้ error หมดไปได้ด้วยการทำให้กราฟทั้ง 2 แยกออกห่างจากกัน และทำได้โดยการเพิ่มค่า g ถ้าเราปรับให้ค่า g ของแต่ละเฟรมสอดคล้องกับ  ผลที่ได้คือไม่มี error ทางฝั่งรับข้อมูล (ต่อจากนี้ ค่า g จะเปลี่ยนไปในแต่ละเฟรม เราจะเขียนแทน g ของแต่ละเฟรมด้วย gm) วิธีกำหนดค่า g อาจทำโดย ถ้า βm มีเครื่องหมายเดียวกับ am ค่า gm เป็นค่าบวกเท่าไรก็ได้ แต่ถ้า βm มีเครื่องหมายตรงกันข้ามกับ am ก็กำหนดให้ค่า gm = -βm/am อย่างไรก็ตาม ในทางปฏิบัติ ช่องทางสื่อสารก็จะเพิ่ม noise เข้ามาอีกอยู่ดี ฉะนั้น เวกเตอร์ที่ฝั่งรับได้รับจึงไม่ใช่ ym แต่เป็น ym+pm ทำให้  จึงต้องมีการเพิ่มระยะ Δg เข้าไปด้วย (Δg กำหนดจากความแปรปรวนโดยประมาณของสัญญาณรบกวนของช่องทางสื่อสาร) เพื่อความมั่นใจและปลอดภัยว่าระบบยังคงเป็น error-free ฉะนั้น gm จะต้องผ่านเงื่อนไข  รูปด้านล่างแสดง inform watermarking ของเวกเตอร์เสียง x ที่ถูกฝังด้วย "1" ได้ผลลัพธ์เป็นเวกเตอร์ y = gv + x = gc + x ซึ่งเราต้องเลือกค่า g เพื่อทำให้ y ตกอยู่ในพื้นที่แรเงาสีเทาขวามือ (ถ้าไม่ตกในพื้นที่นี้ ตัวรับจะไม่อ่านได้ค่า "1") รูปแสดงรายละเอียด 2 กรณี กรณีแรก x(1) เราเลือกค่า g ที่ไม่ติดลบอะไรก็ได้ เช่น 0 เวกเตอร์ y ก็ตกอยู่ในพื้นที่สีเทา สำหรับกรณีที่สอง x(2) เราต้องเลือกเค่า g สูง ๆ และเพื่อรองรับ noise อื่น ๆ ในช่องทางสื่อสาร ระยะห่าง 2Δg ถูกนำมาใช้เป็นช่องว่างระหว่างการตัดสินใจ "1" หรือ "0" ของฝั่งรับ  แน่นอนครับ ปัญหาที่เกิดจากการทำให้ error-free ด้วยวิธีนี้คือ คุณภาพเสียงของ y จะต่ำและเสียงผิดเพี้ยนจากการเพิ่ม gv ที่ g มาก ๆ เข้ากับ x ทางออกต่อปัญหานี้คือใช้สมบัติรับรู้เสียงของมนุษย์เข้ามาช่วยทำให้เราไม่ได้ยินข้อมูล watermark วิธีการคือ เราใช้ Psychoacoustic Model (PAM) มาช่วยในการคำนวณ masking threshold (รายละเอียดของ PAM ผมจะเขียนถึงในบล็อกตอนอื่นนะครับ และเนื้อหาตามหนังสือบทนี้ ผู้เขียนถือว่าผู้อ่านรู้จัก PAM มาเป็นอย่างดีแล้ว) นั่นคือ ถ้า PSD ของ watermark Sw(f) อยู่ต่ำกว่า PSD ของ masking threshold Φ(f) มันจะทำให้เราไม่ได้ยิน watermark หรือพูดอีกอย่างหนึ่งว่า เสียงต้นฉบับไม่ถูกรบกวน และเนื่องจากประสิทธิภาพของระบบ watermarking เป็นฟังก์ชั่นของ SNR ฉะนั้น ประสิทธิภาพดีสุดที่เกิดขึ้นที่ Sw(f) = Φ(f) เราสามารถทำได้โดยเอาฟิลเตอร์ที่จะดัดแปลงองค์ประกอบความถี่ตามการรับรู้ G(f) หรือ perceptual shaping filter ไปแทนที่ gain g ดังรูป 
ถ้า v(n) ของฟิลเตอร์มีลักษณะแบบเดียวกับ white noise (ค่าเฉลี่ยเท่ากับศูนย์และความแปรปรวนสม่ำเสมอ) การปรับสัมประสิทธิ์ของฟิลเตอร์เพื่อให้ output w(n) ของมันมี PSD Sw(f) นั้น เป็นปัญหาสังเคราะห์หรือปัญหาออกแบบฟิลเตอร์ทั่ว ๆ ไป (แก้ชุดของสมการเชิงเส้น Yule-Walker) ทางด้านฝั่งรับ ก็ต้องเพิ่ม G-1(f) ก่อน demodulator แต่ทีนี้มีปัญหาว่า ฝังรับไม่มี x(n) (เป็น watermarking ชนิด blind) ซึ่ง x(n) เป็นตัวที่เราใช้สร้าง G(f) ฉะนั้น G-1(f) จึงต้องสร้างขึ้นมาแบบประมาณ ๆ จาก y(n) โดยความแม่นยำของตัว G-1(f) แบบประมาณนี้ขึ้นอยู่กับ 1. robustness ของ PAM ต่อ watermark และ 2. noise อื่น ๆ ในช่องทางสื่อสาร หลังจากนั้น เราคำนวณ bm คล้ายเดิม แต่คราวนี้เราดูเครื่องหมายของ <zm,c> แทน เมื่อ z(n) คือ output ของ G-1(f) ถ้าเราถือว่าหรือสมมติว่า G-1(f) ที่อยู่ ณ ฝั่งรับนั้นสามารถถูกสร้างให้เป็นอินเวิร์สของ G(f) ได้จริง ๆ เราจะได้ zm = vm + rm เมื่อ r(n) คือ x(n) หลังจากผ่าน G-1(f) การใช้ G-1(f) (มีชื่อเรียก zero-forcing equalizer) จะส่งผลให้ SNR ที่ output ของมันมีค่าต่ำมาก กล่าวคือ กำลังงานของสัญญาณ v(n) มีค่าน้อย ๆ เมื่อเทียบกับกำลังงานของสัญญาณเสียงที่ผ่าน equalizer หรือ r(n) เนื่องจาก PSD ของ v(n) กับ r(n) แตกต่างกัน ดังนั้น จึงเป็นไปได้ที่จะฟิลเตอร์ z(n) ในแบบที่ผลลัพธ์จากการฟิลเตอร์เพิ่มค่า SNR ซึ่งทำได้โดยการขยายองค์ประกอบสเปกตรัมของ z(n) ที่อยู่ภายใต้ v(n) และลดทอนองค์ประกอบสเปกตรัมของ z(n) ที่อยู่ภายใต้ r(n) หน้าที่ดังกล่าวเป็นของ FIR Wiener filter H(z) ดังรูปข้างบนที่เราเอาไปต่อท้าย G-1(f) ในส่วนของการออกแบบฟิลเตอร์ผมจะเขียนถึงอีกทีในบล็อกตอนอื่น อันที่จริง เนื้อหาในบทนี้ หลังจากผู้เขียนแนะนำ Wiener filter แสดงสมการ transfer function กับ ชุดสมการ Wiener-Hopf แล้วก็จบในภาคทฤษฎีเลยครับ |
บทความทั้งหมด
|
 |
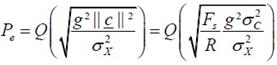
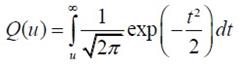






 ผู้ติดตามบล็อก : 85 คน [
ผู้ติดตามบล็อก : 85 คน [