Least Squares
[สารบัญกลุ่มเรื่องที่กำลังศึกษา]
เป็นหลักการหนึ่งที่ใช้บ่อยใน DSP สมมติว่าเรามีฟังก์ชั่นต่อเนื่อง 2 ฟังก์ชั่น f(t) กับ f̂(c,t) เมื่อ c ไม่เป็นฟังก์ชั่นของ t ถ้าเราเลือก c ที่ทำให้ f̂(c,t) เป็นการประมาณแบบ least-squares ของ f(t) ในช่วง t1 ถึง t2 แล้ว total squared error (TSE) ซึ่งมีค่าตามสมการ
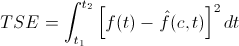
จะมีค่าต่ำสุด
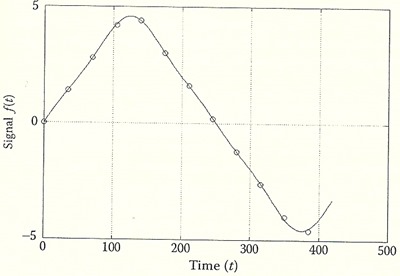
ตัวอย่างรูปด้านล่าง f(t) เป็นคลื่นสามเหลี่ยมมีคาบ = 500 และพล็อตในช่วง t1 = 0 ถึง t2 = 1000 อีกฟังก์ชั่นหนึ่ง f̂(c,t) = c sin(2πt/500) ที่เลือกค่า c ให้ TSE ต่ำสุด เท่ากับเราพูดว่า f̂(c,t) เป็นการประมาณแบบ least-squares ของ f(t) ในช่วง [t1, t2] = [0, 1000]
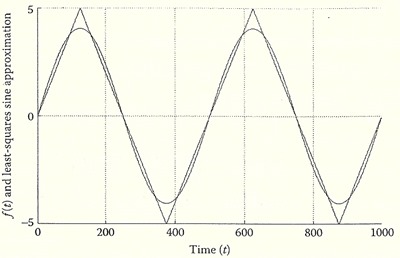
กรณีสัญญาณไม่ต่อเนื่อง f(t) จะกลายเป็นเวกเตอร์ที่มี elements เป็นแซมเปิ้ล N ตัว f = [f1 f2 ··· fN] และสมการ TSE เปลี่ยนเป็น
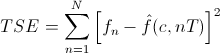
เมื่อ fn คือ element ที่ n ของ f และ T คือ time step หรือช่วงระหว่างแซมเปิ้ล ตัวอย่างรูปด้านล่างคือกรณีไม่ต่อเนื่องของรูปบนที่ T = 35, N = 28
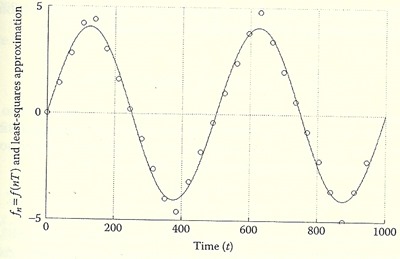
ถ้า f̂(c,t) เป็นฟังก์ชั่นเชิงเส้นของ c เช่น f̂(c,t) = c1 + c2t + c3t2 + ... + cMtM-1 เราจะเรียกว่าเป็นการประมาณแบบ least-squares ที่เป็นเชิงเส้น (linear least-squares approximation) ในกรณีดังกล่าว มีฟังก์ชั่นในรูป tm (ค่าของ m เริ่มจาก 0) อยู่ M ฟังก์ชั่น ถ้าให้ gm(t) เป็นฟังก์ชั่นของ t ฟังก์ชั่นที่ m เราจะเขียน gmn = gm(nT) แทนค่าของ gm(t) ที่ t = nT ฉะนั้น
f̂(c,nT) = c1g1n + c2g2n + c3g3n + ... + cMgMn
และ
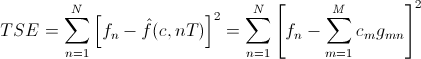
เงื่อนไขที่ทำให้ TSE ต่ำสุดคือ
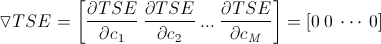
ทั้งหมดจะมี M สมการที่ต้องแก้ออกมาเพื่อหาเวกเตอร์ least-squares coefficient หรือ c = [c1 c2 ··· cM]′, เอาแบบไม่สนใจการจัดรูปทางคณิตศาสตร์นะครับ เราจะได้ c = (G′*G)∖(f*G)′ เมื่อ G = [G′1 G′2 ··· G′M], Gm = [gm1 gm2 ··· gmN], f = [f1 f2 ··· fN], '*' แทน การคูณเวกเตอร์, '′' แทน transpose และ '∖' คือ ตัวดำเนินการที่แก้ชุดของสมการเชิงเส้น เช่น ถ้า B = A∖C แล้ว A*B = C
ลองมาดูตัวอย่างกัน จากรูปบน เลือกมา 12 แซมเปิ้ล เราสร้างเป็น f = [f1 f2 ··· fN] ที่ N = 12 ได้ f = [0.0 1.4 2.8 4.2 4.4 3.0 1.6 0.2 -1.2 -2.6 -4.0 -4.6] คราวนี้ f̂(c,t) เราจะไม่ใช้แค่ฟังก์ชั่น sine ตัวเดียวเหมือนในรูปแล้ว แต่จะใช้ผลรวมของ sine สามตัวแทน
f̂(c,t) = c1sin(2πnT/500) + c2sin(6πnT/500) + c3sin(10πnT/500)
เมื่อ n = 0..11, gmn = sin(2π(2m-1)nT/500) ฉะนั้น เมตริกซ์ G มี 3 หลัก (M = 3) และ 12 แถว (N = 12) โค้ด MATLAB ต่อไปนี้ใช้สร้าง G
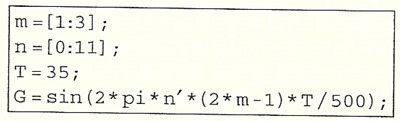
หลังจากได้ G12x3 เราก็คำนวณหา c ได้ตามสูตรครับ

ที่มา: หัวข้อ 2.2 Least Squares หนังสือ Digital Signal Processing with Examples in MATLAB ของ S. D. Stearns กับ D. R. Hush
| Create Date : 28 กรกฎาคม 2556 |
| Last Update : 28 กรกฎาคม 2556 16:33:55 น. |
|
0 comments
|
| Counter : 1985 Pageviews. |
 |
|
|
|
|

