ข้อสอบเข้า Kobe University, Science Course ปี 1998 วิชาแคลคูลัส
มีโจทย์คณิตศาสตร์ข้อหนึ่งที่ผมเห็นว่าน่าสนใจดี เคยนำไปโพสถามไว้ที่พันทิปห้องหว้ากอหลายครั้ง แต่ก็ยังไม่มีใครหาคำตอบหรือแสดงวิธีคิดที่ถูกต้องได้ จนกระทั่งครั้งสุดท้ายคุณ"ผลึกความคิด"สามารถหาคำตอบออกมาได้สำเร็จด้วยแนวคิดที่น่าสนใจทีเดียว แต่ก็เป็นที่ถกเถียงกันเล็กน้อยว่าวิธีที่คุณผลึกความคิดใช้นั้นถูกต้องจริงหรือเปล่า แต่ก่อนอื่นเรามาดูหน้าตาของโจทย์ที่ว่ากันก่อนครับ
กำหนดให้ An = จำนวนของจำนวนเต็ม k ทั้งหมดที่จำนวนหลักของ 7k-1 เท่ากับจำนวนหลักของ 7k (เมื่อเขียนด้วยเลขฐานสิบ) โดยที่ 2 ฃ k ฃ n จงหาค่าของ lim n-->ฅ An/n
ดูเหมือนจะยากพอสมควรเลยใช่ไหมครับ ซึ่งก็คงยากจริงๆนั่นแหละ ไม่งั้นคงมีคนตอบถูกตั้งแต่การโพสครั้งแรกแล้วล่ะครับ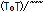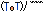 (พันทิปห้องหว้ากอเป็นศูนย์รวมคนเก่งด้านวิทยาศาสตร์ไว้มากมาย ซึ่งรวมไปถึงคนเก่งคณิตศาสตร์ที่เป็นขาประจำเล่นอยู่ห้องนั้นหลายๆคนด้วย) และถ้าคุณลองได้อ่านเฉลยแล้วล่ะก็คงจะเห็นตรงกับผมว่าคนที่สามารถแก้โจทย์ข้อนี้ออกได้ด้วยตัวเองโดยไม่รู้แนวทางหรือเคยเห็นโจทย์คล้ายๆกันมาก่อนต้องเป็นคนที่มีจินตนาการหรือsenseทางคณิตศาสตร์ดีทีเดียวครับ สำหรับวิธีคิดเท่าที่ผมรวบรวมมาจากคำตอบของเพื่อนๆสมาชิกหว้ากอและวิธีคิดจากเฉลยที่ผมมีอยู่กับตัวทั้งหมดก็มีแค่ 3 วิธีซึ่งได้แก่
1. วิธีคิดแบบอุปนัย เป็นวิธีคิดของสมาชิกในหว้ากอท่านหนึ่ง น่าเสียดายที่ผมจำไม่ได้แล้วว่าเป็นใคร ต้องบอกไว้ตั้งแต่ตรงนี้เลยว่าวิธีคิดนี้ผิดครับ ผิดทั้งคำตอบและวิธีทำเลย แต่ถึงจะผิดผมก็อยากนำเสนอไว้เพราะมันเป็นตัวอย่างที่แสดงให้เห็นถึงความผิดพลาดทางคณิตศาสตร์ที่เกิดจากการใช้เหตุผลแบบอุปนัย สำหรับวิธีนี้ ก็เริ่มจากการทดลองหาค่า An ออกมาหลายๆค่าก่อนเพื่อสังเกตรูปแบบของมัน
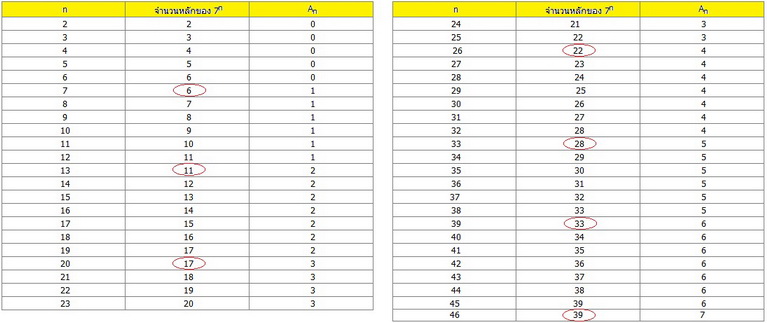
จะเห็นว่า A7 = 1 , A13 = 2 , A20 = 3 , A26 = 4 , A33 = 5 , A39 = 6 , A46 = 7, ... และ(น่าจะ)เป็นในลักษณะนี้ไปเรื่อยๆ จึงสรุปได้ว่า A13n/2 = n เมื่อ n เป็นจำนวนคู่บวกใดๆ (และ A7+13(n-1)/2 = n เมื่อ n เป็นจำนวนคี่บวกใดๆ) ซึ่งข้อสรุปนี้เองที่เป็นจุดผิดพลาดของวิธีคิดแบบอุปนัย เพราะไม่มีอะไรมายืนยันได้เลยว่ามันจะอยู่ในรูปแบบนั้นต่อไปเรื่อยๆ เราจึงไม่สามารถด่วนสรุปไปแบบนั้นได้ อันที่จริงข้อสรุปนี้ผิดด้วยซ้ำ เพราะถ้าลองหาค่า An ต่อไปมากๆจะพบว่ารูปแบบของมันไม่เหมือนเดิม ถึงแม้ว่าวิธีการสังเกตและคาดเดารูปแบบเพื่อหาคำตอบหรือข้อสรุปจะเป็นวิธีการที่นิยมใช้กัน แต่มันก็มีโอกาสเกิดความผิดพลาดได้เพราะมันเป็นเพียงการสังเกตจากประสบการณ์โดยไม่มีเหตุผลใดๆรองรับ ดังนั้นทางที่ถูกต้องจึงต้องมีการพิสูจน์เพื่อยืนยันข้อสังเกตของเราว่าเป็นจริงด้วย จากข้อสรุป(ที่ผิด)ข้างบนจะได้ว่า lim n-->ฅ An/n = lim m-->ฅ A13m/(13m) = lim m-->ฅ 2m/(13m) = 2/13 ## ถึงแม้ว่าวิธีการหาค่าลิมิตจะไม่ผิดแต่คำตอบที่ได้ก็ไม่ถูกต้องเนื่องจากข้อสรุปที่ผิดก่อนหน้านั่นเอง
2. วิธีคิดแบบอาศัย Squeeze theorem เป็นวิธีคิดตามเฉลยที่ผมมีอยู่กับตัวครับ ซึ่งเฉลยไว้ได้อย่างสวยงามทีเดียว(และแน่นอนว่าถูกต้องสมบูรณ์อย่างไม่มีข้อกังขาด้วย) ในเมื่อมันเป็นโจทย์แคลคูลัสวิธีแก้โจทย์ก็ต้องใช้ทฤษฎีบททางแคลคูลัสจริงไหมครับ? และทฤษฎีบทที่ว่าก็คือ Squeeze theorem นั่นเอง เชื่อว่าคนที่เคยเรียนวิชาแคลคูลัสต้องเคยผ่านตา Squeeze theorem มาบ้างในชื่อทฤษฎีบทแซนวิช แต่คงไม่มีโอกาสได้ใช้มันเท่าไหร่ ให้ m = จำนวนหลักของ 7n แล้วจะได้ว่า 10m-1 ≤ 7n < 10m เพราะฉะนั้น m-1 ≤ n(log107) < m _____(1) เนื่องจาก7เป็นจำนวนที่มี1หลัก เมื่อนำ7มาคูณต่อไปเรื่อยๆ ถ้าการคูณ1ครั้งทำให้จำนวนหลักเพิ่มขึ้น1หลัก ก็จะได้ว่า 7n เป็นจำนวนที่มี n หลัก แต่เนื่องจากมีอยู่ An ครั้งที่คูณแล้วไม่ทำให้จำนวนหลักเพิ่มขึ้น ดังนั้น 7n เป็นจำนวนที่มี n - An หลัก นั่นคือ m = n - An
แทนค่า m ใน (1) จะได้ n - An - 1 ≤ n(log107) < n - An n - 1 ≤ An + n(log107) < n n - n(log107) - 1≤ An < n - n(log107) 1 - log107 - 1/n ≤ An/n < 1 - log107 เนื่องจาก lim n -->ฅ {1- log107 - 1/n} = 1 - log107 และ lim n-->ฅ {1 - log107} = 1 - log107 โดย Squeeze theorem จะได้ว่า lim n-->ฅ An/n = 1- log107 ## วิธีในเฉลยก็ไม่ได้ซับซ้อนจนเกินไป ออกจะเรียบง่ายดีด้วย(ในความรู้สึกผมนะ) แต่จุดที่ทำให้โจทย์ข้อนี้ไม่ค่อยมีคนตอบถูกคงเป็นเพราะการใช้ Squeeze theorem ที่หลายคนไม่ค่อยคุ้นเคยกับการเขียนจำนวนหลักของ 7n ให้อยูในรูป An ที่อาจจะทำให้นึกไม่ถึงกันล่ะมั้งครับ
3. วิธีคิดแบบอาศัย fractional part ปิดท้ายด้วยวิธีคิดของคุณผลึกความคิดครับ ถึงแม้จะไม่อาจบอกได้ว่าถูกต้องสมบูรณ์ แต่จัดว่าเป็นวิธีที่น่าทึ่งเลยล่ะและคำตอบก็ออกมาถูกซะด้วย ผมเองก็ไม่ทราบเหมือนกันว่าอะไรดลใจให้เขานึกวิธีแบบนี้ออกมาได้ เรามาดูกันเลยดีกว่า
สำหรับจำนวนจริง x เราให้ [x] แทนจำนวนเต็มที่มากที่สุดที่น้อยกว่าหรือเท่ากับ x และให้ {x} แทน fractional part ของ x นั่นคือ {x} = x - [x]
สำหรับจำนวนเต็มบวก k ใดๆ จะได้ว่า 0 < {k(log107)} < 1 นั่นคือทุกจำนวนเต็มบวก k ค่าของ {k(log107)} จะกระจายตัวอยู่บนช่วง (0,1)
และถ้าจำนวนเต็มบวก k มีคุณสมบัติว่า จำนวนหลักของ 7k-1 เท่ากับจำนวนหลักของ 7k (ต่อไปจะขอเรียกสั้นๆว่าคุณสมบัติQ) แล้ว [k(log107)] = [(k-1)(log107)] ดังนั้น {k(log107)} = k(log107) - [k(log107)] = (k-1)(log107) - [(k-1)(log107)] + log107 = {(k-1)(log107)} + log107 > log107 เพราะ {(k-1)(log107)} > 0 สรุปสั้นๆคือ ถ้าจำนวนเต็มบวก k มีคุณสมบัติQ แล้ว {k(log107)} > log107 และพิสูจน์ได้ไม่ยากว่าในทางกลับกัน (converse) ก็เป็นจริง นั่นคือ ค่าของ {k(log107)} จะกระจายตัวอยู่บนช่วง (log107,1) ก็ต่อเมื่อ จำนวนเต็มบวก k มีคุณสมบัติQ
เนื่องจาก lim n-->ฅ An/n คือสัดส่วนของจำนวนที่มีคุณสมบัติQกับจำนวนเต็มทั้งหมด (หรืออาจจะคิดอีกแบบก็ได้ว่า lim n-->ฅ An/n คือความน่าจะเป็นที่สุ่มจำนวนเต็มบวกมาหนึ่งตัวแล้วได้จำนวนที่มีคุณสมบัติQ) นอกจากนี้จะเห็นว่า จำนวนเต็มบวก k ทั้งหมดสมนัยแบบหนึ่งต่อหนึ่งกับจำนวนอตรรกยะ {k(log107)} บนช่วง (0,1) และจำนวนเต็มบวก k ที่สอดคล้องกับคุณสมบัติQ สมนัยแบบหนึ่งต่อหนึ่งกับ {k(log107)} บนช่วง (log107,1) ดังนั้น ถ้าหากการกระจายตัวของ {k(log107)} เป็นไปอย่างสม่ำเสมอบนช่วง (0,1) เราก็จะสรุปได้ว่า lim n-->ฅ An/n = ความยาวของช่วง(log107,1) / ความยาวของช่วง(0,1) = 1 - log107 ##
จะเห็นว่าเป็นคำตอบที่ถูกต้องตรงกับเฉลย แต่จุดผิดพลาดคือคุณผลึกความคิดอ้างมาลอยๆว่าการกระจายตัวดังกล่าวเป็นไปอย่างสม่ำเสมอโดยไม่ได้พิสูจน์หรือยกทฤษฎีบทที่เกี่ยวข้องมาใช้ จึงทำให้เกิดข้อสงสัยและมีคนทักท้วงคุณผลึกความคิดไปว่า เขาทราบได้อย่างไรว่ามันกระจายตัวสม่ำเสมอ?? อันนี้สำคัญมากครับเพราะกว่าเค้าจะพิสูจน์ว่าเลขหลังทศนิยมของค่า pi กระจายตัวอย่างสม่ำเสมอได้ก็ลำบากอยู่ไม่ใช่น้อย อันที่จริงการพิสูจน์ว่าการกระจายตัวของ {k(log107)} เป็นไปอย่างสม่ำเสมอน่าจะยุ่งยากซับซ้อนมากครับ และอาจจำเป็นต้องใช้คณิตศาสตร์ระดับสูงเช่น Measure Theory มาเกี่ยวข้องก็ได้ คุณผลึกความคิดเองก็ยอมรับว่าเขาตัดสินเอาจากการสังเกตและความรู้สึกยังไม่ได้คิดเรื่องพิสูจน์ออกมาเป็นเรื่องเป็นราว แต่สุดท้ายเขาก็ได้ไปค้นหาทฤษฎีบทที่เกี่ยวข้องคือEquidistribution Theorem มายืนยันแนวคิดของเขาได้เป็นที่เรียบร้อยครับ
หมายเหตุ : โจทย์ข้อนี้เป็นข้อสอบเข้า Kobe University, Science Course ปี 1998 ได้มาจากหนังสือ 100 โจทย์คณิตพิชิต Admission ของสำนักพิมพ์ ส.ส.ท. ครับ
| Create Date : 29 พฤษภาคม 2556 |
| Last Update : 8 กันยายน 2556 19:22:35 น. |
|
0 comments
|
| Counter : 2148 Pageviews. |
 |
|
ฝากข้อความหลังไมค์
Rss Feed
ผู้ติดตามบล็อก : 3 คน [
(พันทิปห้องหว้ากอเป็นศูนย์รวมคนเก่งด้านวิทยาศาสตร์ไว้มากมาย ซึ่งรวมไปถึงคนเก่งคณิตศาสตร์ที่เป็นขาประจำเล่นอยู่ห้องนั้นหลายๆคนด้วย) และถ้าคุณลองได้อ่านเฉลยแล้วล่ะก็คงจะเห็นตรงกับผมว่าคนที่สามารถแก้โจทย์ข้อนี้ออกได้ด้วยตัวเองโดยไม่รู้แนวทางหรือเคยเห็นโจทย์คล้ายๆกันมาก่อนต้องเป็นคนที่มีจินตนาการหรือsenseทางคณิตศาสตร์ดีทีเดียวครับ